디지털 시스템은 정보를 0과 1의 이진 값으로 표현하며, 컴퓨터, 스마트폰, 통신, 의료 등 다양한 분야에서 활용된다. 아날로그와 달리 이산적인 신호를 사용하여 높은 신뢰성과 빠른 연산 속도를 제공한다. 이진수는 디지털 시스템의 기본 연산 단위로, 십진수 대신 2진법을 사용하여 데이터를 저장하고 처리한다. 또한, 8진수와 16진수는 긴 이진수를 간결하게 표현하는 방식으로 활용된다. 디지털 시스템과 이진수의 개념은 현대 기술 발전의 핵심이며, 컴퓨터 공학 및 IT 분야에서 필수적인 기초 지식이다.
1. Digital Systems and Binary Numbers
1.1 이진 체계 (Binary system)
이진수는 디지털 시스템에서 정보를 표현하는 기본적인 방식으로, 0과 1 두 개의 숫자만을 사용한다. 이는 우리가 일반적으로 사용하는 십진수(0~9)와 다르게, 각 자리의 값이 2의 거듭제곱을 따른다. 예를 들어, 십진수 13은 이진수로 변환하면 1101(1×2³ + 1×2² + 0×2¹ + 1×2⁰)로 표현된다. 컴퓨터는 이러한 이진수를 이용해 연산을 수행하고 데이터를 저장하며, 메모리나 프로세서 내부에서도 모든 정보는 이진수 형태로 변환되어 처리된다.

기수 변환은 한 수 체계를 다른 수 체계로 변환하는 과정이다. 십진수를 이진수로 변환하려면 2로 나누어 나머지를 기록하고, 몫이 0이 될 때까지 반복하면 된다. 예를 들어, 십진수 41을 이진수로 변환하면 101001이 된다. 반대로, 이진수를 십진수로 변환하려면 각 자리 값을 2의 거듭제곱으로 계산하면 된다.
또한, 긴 이진수를 간결하게 표현하기 위해 8진수와 16진수가 사용되는데, 8진수는 3비트(2³), 16진수는 4비트(2⁴)를 묶어 변환하는 방식이다. 예를 들어, 이진수 11011001은 8진수로 331, 16진수로 D9로 변환된다. 이러한 기수 변환은 컴퓨터 시스템에서 효율적인 데이터 표현과 저장을 위해 필수적으로 사용된다.

1. 십진수 소수를 이진수로 변환하는 방법
십진수 소수를 2로 곱하는 방식을 사용하여 변환한다.
변환 과정
- 소수 부분에 2를 곱한다.
- 곱한 결과의 정수 부분을 취한다.
- 나머지 소수 부분을 다시 2로 곱한다.
- 이 과정을 원하는 정밀도까지 반복한다.
예제 : (0.6875)₁₀ → 이진수 변환
- 0.6875 × 2 = 1.375 → 정수 부분: 1, 소수 부분: 0.375
- 0.375 × 2 = 0.75 → 정수 부분: 0, 소수 부분: 0.75
- 0.75 × 2 = 1.5 → 정수 부분: 1, 소수 부분: 0.5
- 0.5 × 2 = 1.0 → 정수 부분: 1, 소수 부분: 0 (종료)
따라서, (0.6875)₁₀ = (0.1011)₂

8진수(Octal)와 16진수(Hexadecimal)는 긴 이진수를 보다 간결하게 표현하기 위해 사용되는 기수 체계이다. 8진수는 0부터 7까지의 숫자를 사용하며, 각 8진수 자리는 정확히 3비트(2³)에 해당하므로 이진수 변환이 쉽다. 예를 들어, 이진수 (101 110 001)₂는 8진수 (561)₈로 변환된다. 16진수는 0부터 9까지의 숫자와 A(10)~F(15)를 사용하며, 각 16진수 자리는 4비트(2⁴)와 대응되므로 이진수 표현을 더욱 간결하게 만든다. 예를 들어, 이진수 (1011 1100)₂는 16진수 (BC)₁₆로 변환된다.
1.2 디지털 연산
1.2.1 보수 (Complement)
보수는 디지털 컴퓨터에서 뺄셈 연산을 단순화하고 논리 연산을 효율적으로 수행하기 위해 사용되는 개념으로, 기수 보수(radix complement, r’s complement)와 감소된 기수 보수(diminished radix complement, (r-1)’s complement) 두 가지가 있다. 감소된 기수 보수는 주어진 n자리 숫자 N에 대해 (rⁿ - 1 - N)으로 정의되며, 1의 보수(One’s Complement)와 9의 보수(9’s Complement)가 그 예시다. 기수 보수는 감소된 기수 보수에 1을 추가한 형태로, 2의 보수(Two’s Complement)와 10의 보수(10’s Complement)가 이에 해당한다. 보수를 이용하면 뺄셈을 덧셈으로 변환할 수 있어 하드웨어 구현이 단순해지고, 연산 속도를 향상시키는 장점이 있다.
1의 보수(One’s Complement)
1의 보수는 주어진 이진수에서 모든 비트를 반전(Complement)하여 0을 1로, 1을 0으로 변환하는 방식이다. 예를 들어,
- (1011000)₂의 1의 보수는 (0100111)₂
- (0101101)₂의 1의 보수는 (1010010)₂
1의 보수를 이용한 뺄셈은 다음과 같이 수행된다.
- 감수(빼려는 수)의 1의 보수를 구한다.
- 피감수(빼지는 수)와 감수의 1의 보수를 더한다.
- 결과값에 순환자리올림(end-around carry)이 발생하면 이를 다시 더하여 최종 결과를 얻는다.
예를 들어, (1010100)₂ - (1000011)₂을 1의 보수를 이용해 계산하면:
- 감수 1000011의 1의 보수: 0111100
- 피감수 1010100 + 0111100 = 0010000 (순환자리올림 1 발생)
- 순환자리올림을 더하면: 0010000 + 1 = 0010001
2의 보수(Two’s Complement)
2의 보수는 1의 보수를 먼저 구한 후, 거기에 1을 더하는 방식으로 얻어진다. 예를 들어,
- (1101100)₂의 2의 보수는 (0010100)₂
- (0110111)₂의 2의 보수는 (1001001)₂
2의 보수를 사용하면 순환자리올림을 추가로 더할 필요 없이, 단순한 덧셈 연산만으로 뺄셈이 가능하다.
예를 들어, (1010100)₂ - (1000011)₂을 2의 보수를 이용해 계산하면:
- 감수 1000011의 2의 보수: 0111101
- 피감수 1010100 + 0111101 = 0010001 (올림 발생, 하지만 무시)
- 최종 결과: (0010001)₂
2의 보수 방식은 연산이 간단하고, 1의 보수 방식과 달리 중복된 0(+0과 -0)이 존재하지 않으므로 컴퓨터에서 가장 널리 사용된다.
1.2.2 부호 있는 이진수(Signed Binary Numbers)
컴퓨터에서 음수를 표현하기 위해서는 부호(sign) 정보를 함께 저장해야 한다. 대표적으로 부호-크기(Sign-Magnitude), 1의 보수(Signed-One’s Complement), 2의 보수(Signed-Two’s Complement) 방식이 있다.
1) 부호-크기 방식(Sign-Magnitude)
부호-크기 방식에서는 이진수의 가장 왼쪽 비트를 부호 비트로 사용하며,
- 0이면 양수,
- 1이면 음수를 의미한다.
예를 들어,
- +9는 (00001001)₂
- -9는 (10001001)₂
이 방식은 사람이 이해하기 쉽지만, 덧셈과 뺄셈을 수행할 때 부호를 따로 고려해야 하므로 컴퓨터 연산에는 부적합하다.
2) 1의 보수 방식(Signed-One’s Complement)
1의 보수 방식에서는 양의 정수는 그대로 유지하고, 음의 정수는 해당 수의 1의 보수로 표현한다.
예를 들어,
- +9는 (00001001)₂
- -9는 (11110110)₂ (1의 보수를 취한 결과)
이 방식에서는 0을 두 가지로 표현할 수 있는 문제가 있다. 즉,
- (+0) = (00000000)₂
- (-0) = (11111111)₂
또한, 덧셈과 뺄셈을 수행할 때 순환자리올림(end-around carry)을 더해야 하는 불편함이 있다.
3) 2의 보수 방식(Signed-Two’s Complement)
2의 보수 방식은 음수를 표현할 때 1의 보수를 구한 후 1을 더하는 방식이다.
예를 들어,
- +9는 (00001001)₂
- -9는 (11110111)₂ (1의 보수(11110110) + 1)
이 방식은 덧셈과 뺄셈 연산이 단순해지고, 0이 한 가지 형태(00000000)로만 표현된다는 장점이 있어, 현대 컴퓨터에서 가장 널리 사용된다.
2의 보수를 이용한 뺄셈 예제
문제: (–6) - (–13) = ?
- (–6)의 2의 보수 표현: 11111010
- (–13)의 2의 보수 표현: 11110011
- (-6) - (-13) = (-6) + (+13) → 11111010 + 00001101
- 결과: 00000111 (7)
이처럼 2의 보수를 사용하면 덧셈만으로도 뺄셈이 가능하므로, 연산이 단순해지고 하드웨어 구현이 쉬워진다.
1.3 Binary Code and Logic
1.3.1 Binary Code
이진 코드(Binary Codes)는 단순한 이진수(Binary Number)와는 다르다. 이진수는 수의 표현을 위한 체계인 반면, 이진 코드는 정보를 표현하기 위한 규칙적인 비트 조합이다. 예를 들어, n비트 이진 코드는 1과 0의 조합으로 최대 2ⁿ개의 서로 다른 상태를 표현할 수 있다. 컴퓨터는 이진수 기반의 연산이 자연스럽지만, 인간은 10진수에 익숙하다. 이 차이를 극복하기 위해 10진수를 이진수로 변환하여 연산하고, 결과를 다시 10진수로 변환하는 방식이 사용된다.
컴퓨터는 이진수만을 인식하므로, 10진 숫자를 이진 코드로 변환하여 처리해야 한다. 이때 각 10진수 자릿수를 4비트 이진 코드로 표현하는 방식 중 하나가 BCD(Binary-Coded Decimal) 코드이다. 이외에도 Gray 코드, ASCII 코드 등 다양한 이진 코드들이 존재하며, 각각의 목적에 맞게 사용된다.
BCD (Binary-Coded Decimal) 코드

BCD 코드는 각 10진수 자릿수를 4비트 이진수로 표현하는 방식이다. 예를 들어, 10진수 185는 BCD로 (0001 1000 0101)이며, 이는 각 자리수인 1, 8, 5를 각각 4비트로 표현한 것이다. BCD에서는 이진 조합 중 1010(10)~1111(15)는 사용되지 않으며 의미가 없다. 따라서 BCD는 이진수와 유사한 형태를 띠지만, 실제로는 10진수에 기반한 표현 방식이다.

BCD에서 두 자릿수를 더할 때, 그 합이 1010(10)이상이 되면 이는 유효하지 않은 BCD 값이 되므로 보정이 필요하다. 이를 위해 6(0110)을 더해줘야 한다. 이는 이진수에서 4비트 자리수의 최대값인 1111(15)와 10진수 자리수의 차이인 6을 이용한 것이다. 이 보정은 자리올림(carry)까지 고려하며 정확한 10진수 결과를 이끌어낸다.
Gray Code

Gray 코드는 연속된 값 간의 전환 시 오직 한 비트만 변경되는 특징을 갖는다. 예를 들어, 7에서 8로 전환할 때 이진수는 0111에서 1000으로 4비트가 모두 바뀌지만, Gray 코드는 0100에서 1100으로 단 한 비트만 바뀐다. 이 특성은 센서나 디지털 회로에서 전이 과정에서의 오류 가능성을 줄이는 데 유리하다.
ASCII (American Standard Code for Information Interchange)

ASCII 코드는 문자 정보를 이진수로 표현하기 위한 표준 코드로, 영문자(대문자+소문자), 숫자, 특수문자 등 총 약 128개의 문자 집합을 7비트로 표현한다. 대부분의 컴퓨터는 8비트를 한 단위(byte)로 처리하므로, 실제 저장은 1바이트 단위로 이뤄진다. ASCII는 통신에서 문자 전송 시 표준화된 방식으로 광범위하게 사용되며, 오류 검출을 위한 패리티 비트(parity bit)가 추가되어 8번째 비트로 활용되기도 한다.
다양한 이진 코드의 종류
표준 BCD 이외에도 다양한 코드들이 존재한다. 예를 들어 2421 코드, Excess-3 코드, 8-4-–2–1 코드 등이 있다.
- Weighted Code: 각 비트에 가중치를 부여하여 10진 값을 계산한다 (예: BCD, 2421).
- Unweighted Code: 가중치 없이 규칙적으로 변환된 코드 (예: Excess-3).
- Self-complementing Code: 어떤 숫자의 보수도 코드 내에서 자동으로 나타나는 특성 (2421, Excess-3).
- Signed Weighted Code: 양수와 음수 가중치를 동시에 사용하는 코드 (예: 8-4-–2–1).
1.3.2 Binary Storage and Registers (2진 기억 장치와 레지스터)

레지스터는 이진 셀들이 연속적으로 모여 형성된 저장 공간으로, 컴퓨터 내부에서 정보를 일시적으로 저장하거나 처리할 때 사용된다. 예를 들어, 16비트 레지스터는 총 2¹⁶개의 상태를 가질 수 있으며, 이진 데이터 1100 0011 1100 1001은 상황에 따라 10진수 50,121로 해석되거나, 문자 'CI' (ASCII 코드), 또는 초과-3 코드(excess-3 code)로 해석될 수 있다. 이처럼 같은 비트 패턴이라도 해석 방식에 따라 전혀 다른 의미를 가질 수 있으며, 이는 응용 프로그램의 목적에 따라 달라진다.
레지스터 간의 정보 이동은 ASCII 코드 기반으로 이뤄지며, 오류 검출을 위해 홀수 패리티 비트(odd-parity bit)가 포함된다. 즉, 각 8비트 문자에는 하나의 패리티 비트가 추가되어 총 9비트로 구성되며, 이 문자가 레지스터로 이동되기 전에는 이전 문자가 왼쪽으로 8칸 이동(shift)되는 과정이 선행된다. 이러한 방식은 연속된 문자를 처리할 때 정확한 순서와 오류 검출을 보장하기 위함이다.
레지스터는 CPU와 메모리 사이에서 정보를 일시적으로 저장하고 전달하는 중간 매개체 역할을 한다. 메모리에 저장된 정보는 프로세서의 레지스터로 이동하여 처리되며, 처리 결과는 다시 메모리 레지스터로 저장될 수 있다. 이러한 구조 덕분에 CPU는 반복적인 계산이나 제어 작업을 빠르게 수행할 수 있으며, 메모리는 연산 결과를 장기적으로 보관하는 데 활용된다.
이진 논리
이진 논리(binary logic)는 두 가지 요소로 구성된다:
- 이진 변수: A, B, C, x, y, z 등 (각 변수는 0 또는 1의 값을 가짐)
- 논리 연산: AND, OR, NOT의 세 가지 기본 연산
이 연산들은 각각 다음과 같은 수학적 의미와 유사하다:
- AND: 곱셈과 유사 (둘 다 1일 때만 1)
- OR: 덧셈과 유사 (하나라도 1이면 1)
- NOT: 입력의 반대값을 출력
진리표는 가능한 모든 변수 조합에 대해 연산 결과를 표로 정리한 것이다. 이를 통해 논리 연산의 동작을 명확히 이해할 수 있다.
예를 들어, 두 변수 A와 B에 대한 AND 연산의 진리표는 다음과 같다:
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
논리 게이트는 전자 회로로 구현된 논리 연산 소자이다. 입력 신호(예: 0V 또는 3V)를 받아 논리 연산을 수행하고 출력 신호를 생성한다. 입력 전압이 특정 범위에 있으면 해당 신호를 0 또는 1로 해석한다. 디지털 회로에서 이러한 신호 처리를 통해 다양한 제어와 계산이 가능하다. 논리 게이트는 기본적으로 다음과 같은 기호로 표현된다:
- AND 게이트: 곱셈 연산
- OR 게이트: 덧셈 연산
- NOT 게이트: 반전
여러 개의 입력을 가지는 게이트도 존재하며, 각각의 동작은 다음과 같다:
- 3입력 AND 게이트: 모든 입력이 1일 때만 출력이 1
- 4입력 OR 게이트: 입력 중 하나라도 1이면 출력이 1, 모두 0일 때만 0
2. Boolean Algebra and Logic Gates
2.1 부울 대수 (Boolean Algebra)

부울 대수(Boolean Algebra)는 디지털 회로를 최적화하고 복잡한 회로 최적화 알고리즘을 이해하는 데 필요한 수학적 방법을 제공한다. 논리 회로를 보다 간결하게 표현하고, 연산의 규칙을 정의하는 데 활용된다. 부울 대수의 기초 개념으로 집합(Set)과 원소(Element) 개념이 있으며, 집합은 공통된 속성을 가진 객체들의 모음이다. 예를 들어, A={1,2,3,4}는 1, 2, 3, 4라는 원소들로 구성된 집합 A를 의미한다. 집합 내의 원소들에 적용되는 연산 규칙을 연산자(Operator)라고 하며, 이는 두 개 이상의 원소를 입력으로 받아 하나의 결과값을 생성하는 규칙을 의미한다. 예를 들어, a∗b = c는 연산자가 *일 때, a와 b라는 두 원소를 연산하여 결과값 c를 도출하는 방식이다.
수학적 체계는 기본적으로 공준(Postulate)과 공리(Axiom)에 의해 형성된다. 공준은 증명 없이 참으로 가정되는 진술로, 이를 바탕으로 수학적 체계 내에서 정리(Theorem)와 성질을 유도할 수 있다. 부울 대수를 비롯한 여러 대수 구조를 정의하는 데 사용되는 대표적인 공준에는 다음과 같은 것들이 있다. (일반적인 대수에서 보편적으로 받아드려지는 공준)
1. 닫힘성(Closure)
집합 S가 어떤 이항 연산(binary operation)에 대해 닫혀 있다는 것은, 의 임의의 원소 와 에 대해 연산을 수행한 결과가 다시 S의 원소로 포함됨을 의미한다.
- 덧셈 연산을 고려한 자연수 집합
- N={0,1,2,3,… }
- 두 자연수의 합은 항상 자연수이다. 예를 들어, 2+3=5이므로 덧셈 연산에 대해 닫혀 있음.
- 하지만 뺄셈의 경우 2−3=−1인데, −1은 자연수에 속하지 않으므로 뺄셈 연산에 대해 닫혀 있지 않음.
2. 결합법칙(Associative Law)
연산을 수행할 때 괄호의 위치를 바꿔도 결과가 변하지 않음을 의미한다.
- 덧셈(+)과 곱셈(×)은 결합법칙이 성립
- (2+3)+4 = 2+(3+4) = 9
- (2×3)×4 = 2×(3×4) = 24
- 뺄셈(-)과 나눗셈(÷)은 결합법칙이 성립하지 않음
- (10−5)−2=5−2=3, 하지만 10−(5−2)=10−3=7이므로 서로 다름.
- (8÷4)÷2=2÷2=1, 하지만 8÷(4÷2)=8÷2=4이므로 서로 다름.
3. 교환법칙(Commutative Law)
연산의 순서를 바꾸어도 결과가 동일함을 의미한다.
- 덧셈(+)과 곱셈(×)은 교환법칙이 성립
- 3+5=5+3=8
- 4×7=7×4=28
- 뺄셈(-)과 나눗셈(÷)은 교환법칙이 성립하지 않음
- 7−3=4이지만 3−7=−4로 결과가 다름.
- 8÷4=2이지만 4÷8=0.5로 다름.
4. 단위 원소(Identity Element)
어떤 연산에 대해 원소 와 결합해도 자체가 유지되는 원소 e를 의미한다.
- 덧셈에서의 단위 원소 → 0
- x+0=0+x=x
- 곱셈에서의 단위 원소 → 1
- x×1=1×x=x
- 뺄셈과 나눗셈에는 단위 원소가 없음
- x−e=x가 성립하는 는 존재하지 않음.
- x÷e=x가 성립하는 는 존재하지 않음.
5. 역원(Inverse)
어떤 원소 에 대해 특정 연산을 수행했을 때 단위 원소가 되는 원소 y가 존재하는 경우를 의미한다.
- 덧셈에서의 역원 → 음수
- x+(−x)=0
- 곱셈에서의 역원 → 역수
- x×1x=1
- 뺄셈과 나눗셈은 역원이 존재하지 않음
- x−y=e가 되는 y를 찾을 수 없음.
- x÷y=e가 되는 를 찾을 수 없음.
6. 분배법칙(Distributive Law)
연산의 우선순위를 조정할 수 있음을 의미하며, 괄호를 해체하거나 묶어서 계산할 수 있는 성질을 말한다.
예시:
- 곱셈과 덧셈에 대한 분배법칙
- x×(y+z)=(x×y)+(x×z)
- 덧셈과 곱셈이 섞인 경우 적용 가능
- (x+y)×z=(x×z)+(y×z)(x + y) \times z = (x \times z) + (y \times z)
예: (3+5)×2=(3×2)+(5×2)(3+5) \times 2 = (3 \times 2) + (5 \times 2)
8×2=6+10=168 \times 2 = 6 + 10 = 16 (성립)
- (x+y)×z=(x×z)+(y×z)(x + y) \times z = (x \times z) + (y \times z)
- 뺄셈과 나눗셈에서는 일반적으로 적용되지 않음
- x−(y+z)≠(x−y)+(x−z)x - (y + z) \neq (x - y) + (x - z)예: 10−(3+2)=10−5=510 - (3+2) = 10 - 5 = 5
그러나 (10−3)+(10−2)=7+8=15(10-3) + (10-2) = 7 + 8 = 15로 다름.
- x−(y+z)≠(x−y)+(x−z)x - (y + z) \neq (x - y) + (x - z)예: 10−(3+2)=10−5=510 - (3+2) = 10 - 5 = 5
2.2 부울 대수의 공리적 정의 (Axiomatic Definition of Boolean Algebra)
부울 대수(Boolean Algebra)는 1854년 George Boole이 개발한 대수 시스템으로, 디지털 논리 회로를 수학적으로 표현하고 최적화하는 데 사용된다. 이후 1904년 E. V. Huntington은 이를 더 공식적으로 정의하기 위해 공리(Postulates)를 정립하였다. 부울 대수는 OR(논리합), AND(논리곱), NOT(보수) 연산을 기반으로 하며, 다음과 같은 여섯 가지 공리를 따른다.
1) 닫힘성(Closure)
어떤 연산이 집합 내의 모든 원소에 대해 수행되었을 때, 그 결과값이 항상 같은 집합 내에 존재하는 성질을 닫힘성(Closure)이라고 한다. 부울 대수에서는 OR 연산(+)과 AND 연산(∙)에 대해 닫힘성이 성립한다. 즉, 부울 집합 B={0,1}B에서 임의의 원소 x,y에 대해, x+y∈B,x⋅y∈B가 성립한다. 예를 들어, 0+1=1이므로, OR과 AND 연산의 결과는 항상 0 또는 1이다. 따라서, 부울 대수는 닫힘성을 만족한다.
2) 단위 원소(Identity Element)
단위 원소란 어떤 연산에서 특정 원소와 결합했을 때도 원래의 값이 유지되는 값을 의미한다. 부울 대수에서는 OR 연산과 AND 연산에 각각 단위 원소가 존재한다.
- OR 연산에서 0은 단위 원소이다.
- AND 연산에서 1은 단위 원소이다.
3) 교환법칙(Commutative Law)
교환법칙이란 연산의 순서를 바꾸어도 결과가 동일함을 의미한다. 부울 대수에서는 OR 연산과 AND 연산 모두 교환법칙을 만족한다. 즉, 부울 대수에서는 OR과 AND 연산의 순서를 바꾸어도 결과가 변하지 않는다.
4) 분배법칙(Distributive Law)
분배법칙이란 연산의 우선순위를 조정할 수 있음을 의미하며, 부울 대수에서는 OR 연산과 AND 연산 모두 분배법칙을 만족한다.
- AND 연산이 OR 연산에 대해 분배된다.x⋅(y+z)=(x⋅y)+(x⋅z) 예를 들어, 1⋅(0+1)=(1⋅0)+(1⋅1)=0+1=1이 성립한다.
- OR 연산이 AND 연산에 대해 분배된다.x+(y⋅z)=(x+y)⋅(x+z)예를 들어, 0+(1⋅1)=(0+1)⋅(0+1)=1⋅1=1이 성립한다.
이처럼 부울 대수에서는 연산의 분배법칙이 일반 대수와 다르게 성립한다.
5) 보수 법칙(Complement Law)
부울 대수에서는 모든 원소 에 대해 보수(complement) x′가 존재하여 다음이 성립한다.
x+x′=1, x⋅x′=0
예를 들어,
- x=1일 때 x′=0이므로, 1+0=1이 성립한다.
- x=0일 때 x′=1이므로, 0+1=1이 성립한다.
즉, 부울 대수에서는 모든 값에 대해 0과 1을 바꾸는 연산(보수 연산)이 존재한다.
6) 서로 다른 최소 두 개의 원소 존재
부울 대수에서는 최소한 두 개의 원소가 존재해야 하며, 이 원소들은 서로 달라야 한다. 즉, 0≠1가 성립해야 한다. 이 조건을 만족하지 않으면, 부울 대수는 의미를 가지지 않는다.
부울 대수와 일반 대수의 차이점
1. Huntington의 공준에는 결합법칙(Associative Law)이 포함되지 않지만, 부울 대수에서는 결합법칙이 성립하며 다른 공리를 이용해 유도할 수 있다.
일반적인 수학 대수에서 결합법칙은 기본적으로 받아들여지는 성질이며, Huntington의 부울 대수 공준 체계에서는 이것을 직접 포함하지 않는다. 그러나 부울 대수에서는 결합법칙이 실제로 성립하며, 이는 다른 공리들을 조합하여 유도할 수 있다. 예를 들어, A+(B+C)=(A+B)+C와 같이 OR 연산에서도 결합이 가능하며, AND 연산도 마찬가지이다.
2. 부울 대수에서는 분배법칙이 일반 대수와 다르게 성립한다.
일반적인 수학 대수에서는 곱셈이 덧셈에 대해 분배되는 성질만 존재하지만, 부울 대수에서는 덧셈(OR)이 곱셈(AND)에 대해 분배되는 법칙도 함께 성립한다. 즉, A+(B⋅C)=(A+B)⋅(A+C)와 같은 형태도 항상 성립한다.
3. 부울 대수에서는 덧셈과 곱셈의 역원이 존재하지 않으므로, 뺄셈과 나눗셈이 정의되지 않는다.
일반 수학 대수에서는 a+(−a)=0 과 같이 덧셈의 역원(음수), a⋅1a=1과 같은 곱셈의 역원(분수)이 존재하여 뺄셈이나 나눗셈이 가능하다. 그러나 부울 대수에서는 이진 값 0과 1만 존재하기 때문에 어떤 값에 대해 그 연산을 무효화할 수 있는 역원이라는 개념이 없다. 따라서 부울 대수에는 뺄셈과 나눗셈 연산 자체가 정의되지 않으며, 논리식의 연산은 항상 OR, AND, NOT으로만 구성된다.
4. 부울 대수에서는 보수(complement) 연산이 존재하지만, 일반 대수에서는 존재하지 않는다.
부울 대수에서는 값을 반대로 뒤집는 보수(complement) 연산, 즉 NOT 연산이 명확히 존재한다. 예를 들어 A가 1이면 A′는 0이 되고, A가 0이면 A′는 1이 된다. 이는 참과 거짓을 서로 바꾸는 단순한 반전 연산으로, 디지털 회로에서는 NOT 게이트로 쉽게 구현된다. 하지만 일반 대수에서는 어떤 수에 대해 이렇게 명확히 반대되는 값을 반환하는 연산이 존재하지 않는다. 예를 들어 5의 반대는 -5라고 할 수 있지만, 이는 보수가 아닌 덧셈의 역원이며, 개념 자체가 다르다. 따라서 보수는 부울 대수에서만 가지는 고유한 개념이다.
5. 일반 대수는 실수와 같은 무한한 원소를 다루지만, 부울 대수는 0과 1 두 개의 원소만을 다룬다.
일반적인 수학 대수에서는 실수, 정수, 유리수 등 무수히 많은 수를 다룬다. 예를 들어, 1과 2 사이에도 무한히 많은 수가 존재하므로 계산도 복잡하고 무한한 경우의 수를 고려해야 한다. 하지만 부울 대수는 단 두 개의 값, 즉 0과 1만 존재하기 때문에 가능한 조합이 유한하다.
2.3 부울 대수의 기본 정리와 성질 (Basic Theorems and Properties of Boolean Algebra)
1. 쌍대 원리 (Duality Principle)
쌍대 원리는 부울 대수의 연산 기호와 항등 원소를 교환해도 동일한 성질이 유지됨을 의미한다. 즉, 다음과 같이 변환할 수 있다.
- OR 연산 (+) ↔ AND 연산
- 0 ↔ 1
예제: 전등 스위치의 논리
전등이 켜지려면 스위치 A 또는 스위치 B가 켜져 있어야 한다고 가정해 보자.
- 일반적인 논리식:
- 전등이 켜지는 조건: A+B=1
- 만약 둘 다 꺼져 있으면 0+0=0 → 전등이 꺼짐
- 쌍대 원리를 적용한 경우:
- 전등이 꺼지려면 스위치 A와 스위치 B가 모두 꺼져 있어야 한다고 표현할 수도 있다.
- 즉, 모든 조건을 AND 연산으로 바꾸면, A⋅B=0
- 이는 전등을 끄는 조건이 된다.
즉, 켜지는 조건을 OR로 표현하면, 꺼지는 조건은 AND로 바꿔서 표현할 수 있다. 이를 통해 부울 대수에서는 동일한 논리를 OR 또는 AND 연산을 사용해 다르게 설명할 수 있다.
2. 항등 법칙 (Identity Law)
어떤 변수에 OR 연산에서 0을 더하거나, AND 연산에서 1을 곱하면, 결과는 원래 변수와 같다.
예제: 비밀번호 입력 시스템
- 상황: 로그인 시스템에서 사용자가 비밀번호를 입력해야 로그인할 수 있다고 가정하자.
- 논리:
- 입력한 비밀번호가 맞다면 , 틀리면 0
- 비밀번호를 입력하지 않으면, 시스템이 자동으로 입력값을 0으로 간주
- 그러면 OR 연산에서 0을 더하는 것은 아무런 영향을 주지 않음
- 즉, 입력하지 않은 것은 로그인 여부에 영향을 미치지 않는다.
반대로, AND 연산에서 1을 곱하는 것은 입력값을 그대로 유지하는 것과 같다.
3. 무효 법칙 (Null Law, Domination Law)
어떤 변수에 OR 연산에서 1을 더하면 항상 1이 되고, AND 연산에서 0을 곱하면 항상 0이 된다.
예제: 자동 도어 시스템
- 상황: 건물 입구에서 자동문이 열리는 조건을 생각해 보자.
- 논리:
- 자동문은 카드 인식 OR 비밀번호 입력 중 하나라도 성공하면 열린다.
- 즉, OR 연산에서 1을 더하면(즉, 항상 카드가 인식된다고 가정하면) 문은 무조건 열린다.
- 반대로, AND 연산에서 0을 곱하면 문이 무조건 닫힘
- 즉, 카드를 대더라도 도어 시스템이 비활성화되면 문이 열리지 않는다.
이처럼 OR에서 1은 무조건 참을, AND에서 0은 무조건 거짓을 의미한다.
4. 항등원 법칙 (Idempotent Law)
같은 변수를 OR 연산하거나 AND 연산하면, 결과는 그대로 유지된다.
예제: 교통 신호 시스템
- 상황: 교통 신호에서 초록불이 켜져야 차량이 출발할 수 있다고 가정하자.
- 논리:
- 초록불이 이미 켜져 있다면, 또 초록불을 켜는 것은 아무런 영향을 주지 않음
- 마찬가지로, 빨간불 상태에서는 여러 번 신호를 확인해도 여전히 빨간불 상태
즉, 같은 상태를 반복해서 적용해도 결과는 변하지 않는다.
5. 보수 법칙 (Complement Law)
어떤 값과 그 보수를 OR 연산하면 항상 1이 되고, AND 연산하면 항상 0이 된다.
현실 예제: 출입 카드 시스템
- 상황: 회사 출입문은 카드를 인식하면 열리고, 인식하지 않으면 닫힌다고 가정하자.
- 논리:
- 카드를 인식했을 때와 안 했을 때를 따로 고려해 보면,
- 문이 열리는 조건은 출입카드+출입카드′=1출입카드 + 출입카드' = 1
- 즉, **카드를 인식한 경우(1) 또는 인식하지 않은 경우(0)**가 존재하므로, 항상 1이 됨.
반대로, AND 연산에서는 무조건 닫힘을 의미한다.
6. 흡수 법칙 (Absorption Law)
특정한 조합의 연산을 단순화할 수 있다.
예제: 공항 보안 시스템
상황: 공항 보안 검색대를 통과하는 조건을 생각해 보자.
논리: 승객이 보안 검사를 통과하려면 탑승권을 소지해야 하며, 추가로 보안 확인이 필요할 수도 있다 이때, 보안 검색을 필수로 해야 한다면, 추가 조건이 의미가 없어짐. 즉, 탑승권+(탑승권⋅보안확인)=탑승권 보안 확인 여부와 관계없이 탑승권만 있으면 출입 가능하므로, 조건이 단순화된다.

2.4 부울 함수 (Boolean Functions)
부울 함수(Boolean Function)는 0과 1로 표현되는 이진 변수(Binary Variables), 논리 연산(AND, OR, NOT), 그리고 상수(0과 1)로 구성된 수학적 표현식이다. 이러한 함수는 디지털 회로에서 특정 연산을 수행하기 위해 사용되며, 다양한 방법으로 표현될 수 있다. 예를 들어, 간단한 부울 함수로 F = A + B가 있다. 이는 A 또는 B 중 하나라도 1이면 출력이 1이 되는 OR 연산을 의미한다.
부울 함수는 세 가지 방식으로 표현될 수 있다:
- Algebraic Expression: 논리 연산 기호를 사용하여 수학적 식으로 나타낸다. 예를 들어, F=AB+A′C는 부울 대수를 이용한 함수 표현이다.
- Truth Table: 모든 입력 조합에 대해 출력 값을 보여주는 표이다. 예를 들어, 두 입력 A와 B에 대해 OR 연산을 수행하는 함수 F=A+B의 진리표는 다음과 같다.
- Logical Circuit : 회로 형태로 표현한 것이다.
논리 회로에서 사용되는 부울 함수는 불필요한 연산을 제거하여 간소화할 수 있다. 이를 부울 대수(Boolean Algebra)를 이용한 최소화라고 한다. 예를 들어, 다음 부울 함수를 보자.

부울 함수의 보수는 DeMorgan의 정리(DeMorgan's Theorem)를 사용하여 구할 수 있다. DeMorgan의 정리

쌍대 원리는 논리곱(AND)과 논리합(OR)을 서로 바꾸고, 0과 1도 서로 바꾸는 개념이다. 예를 들어, 함수 F=A+B의 듀얼은

2.5 Canonical and Standard Forms (정준 형식 및 표준 형식)
부울 함수(Boolean function)는 다양한 방식으로 표현할 수 있는데, 그 중에서도 정준 형식(canonical form)과 표준 형식(standard form)은 디지털 회로 설계에서 자주 사용된다. 정준 형식은 모든 항에 모든 변수가 포함되어 있는 가장 기본적인 형태이며, 최소항(minterm)의 합 또는 최대항(maxterm)의 곱으로 구성된다. 반면 표준 형식은 모든 변수를 반드시 포함할 필요는 없고, 회로 구현을 위해 AND-OR 또는 OR-AND 구조로 정리된 형태를 의미한다.
2.5.1 정준 형식 (Canonical Forms)
정준 표현은 모든 변수를 포함한 형태로 부울 함수를 체계적으로 나타내는 방식이다. 예를 들어, 함수 f1 = x’y’z + xy’z’ + xyz는 세 개의 변수(x, y, z)를 모두 포함한 세 개의 항으로 이루어져 있으며, 각 항은 변수들의 AND 조합으로 구성된다. 이러한 표현은 최소항(Minterm)의 합으로 나타낼 수 있는데, 각 항은 출력이 1이 되는 입력 조합에 대응된다. 이 예시는 f1 = m1 + m4 + m7로도 나타낼 수 있으며, 여기서 m1, m4, m7은 각각 진리표에서 f = 1이 되는 입력 조합의 번호를 의미한다.
이처럼 출력이 1인 입력 조합을 모두 나열하여 OR로 연결한 형식을 최소항의 합(Sum of Minterms)이라고 한다. 예를 들어, F = A + B’C를 최소항으로 바꾸기 위해 각 항을 모든 변수에 대해 확장하는 과정을 거친다. 항 A는 변수 B와 C에 대해 (B + B’)(C + C’)를 곱해 ABC + ABC’ + AB’C + AB’C’로 나타내고, B’C는 A를 기준으로 A’B’C + AB’C로 확장할 수 있다. 이 모든 항을 더하면 F = ABC + ABC’ + AB’C + AB’C’ + A’B’C가 되며, 이는 최소항으로 m1 + m4 + m5 + m6 + m7로 표현된다. 이 방식은 함수의 참값(1)을 나타내는 경우를 중심으로 구조화된 표현이다.
반대로, 출력이 0인 입력 조합을 기준으로 표현한 것이 최대항의 곱(Product of Maxterms)이다. 함수가 참이 아닌(즉, 0이 되는) 입력 조건들을 나열하고, 이를 OR 항으로 표현한 뒤 AND로 연결한다. 예를 들어 F = xy + x’z는 먼저 분배법칙을 사용해 (x + y)(x + z)(x’ + y)(x’ + z’)처럼 OR 항으로 확장한 다음, 각 항에서 누락된 변수를 추가하고 보수형을 고려하여 F = (x + y + z)(x + y’ + z)(x’ + y + z)(x’ + y + z’)로 정리할 수 있다. 이는 최대항으로 Π(0,2,4,5)처럼 간결하게 표현된다. 이 방식은 부울 함수의 거짓값(0)에 해당하는 경우를 중심으로 구조화되어 있다.
이 두 가지 형식은 서로 변환이 가능한데, 이를 정준 형식 간 변환이라 한다. 예를 들어, 최소항의 합으로 주어진 함수 F(A,B,C) = Σ(1,4,5,6,7)이 있을 때, 보수 함수를 먼저 구하면 F’ = Σ(0,2,3)이 된다. 이를 다시 보수하면 F = Π(0,2,3)이라는 최대항의 곱 표현으로 변환된다. 이처럼 mj’ = Mj라는 관계(즉, 최소항의 보수는 해당하는 최대항) 덕분에, 두 정준 표현은 상호 전환이 가능하다.
2.5.2 표준 형식 (Standard Forms)
표준 형식(Standard Form)은 부울 함수를 논리 회로로 쉽게 구현할 수 있도록 단순화한 표현 방식이다. 이는 모든 변수를 포함해야 하는 정준 형식(Canonical Form)과는 달리, 필요한 변수만 포함하여 AND 또는 OR 연산을 중심으로 표현하는 것이 특징이다.
표준 형식에는 크게 두 가지 유형이 있다. 첫 번째는 곱의 합(Sum of Products, SOP) 형식이고, 두 번째는 합의 곱(Product of Sums, POS) 형식이다. SOP 형식은 여러 개의 AND 항(곱 항)을 OR 연산으로 연결한 형태이며, POS 형식은 여러 개의 OR 항(합 항)을 AND 연산으로 연결한 형태이다.
예를 들어, F1 = y’ + xy + x’yz’는 SOP 형식이다. 각 항은 AND 연산을 기반으로 구성되어 있고, 전체 함수는 이들을 OR 연산으로 합친 형태다. 이와 달리, F2 = (y’ + z)(x’ + y + z’)는 POS 형식으로, OR 항들을 괄호로 묶고, 이 항들 전체를 AND 연산으로 연결한 구조다. 이 두 형식은 모두 두 단계의 논리 연산으로 구성되어 있어 two-level implementation에 적합하다.
또한, 함수가 처음 주어졌을 때는 표준 형식이 아닐 수도 있다. 예를 들어, F3 = AB + C(D + E)는 곱과 괄호가 섞여 있어 비표준(non-standard) 구조를 가진다. 하지만 이 함수도 분배법칙을 적용하면 F3 = AB + CD + CE처럼 SOP 구조로 변환할 수 있다. 이렇게 비표준 형식을 표준 형식으로 바꾸는 과정은 논리 회로를 두 단계 게이트로 구성할 수 있게 하며, 회로의 단순성과 구현 효율성을 높여준다.
2.5.3 기타 논리 연산 (2.7 Other Logic Operations)

두 개의 변수로 만들 수 있는 부울 함수는 총 16가지가 존재한다. 일반적으로 많이 사용하는 AND와 OR 연산은 이 중 두 가지에 불과하며, 나머지 14개의 함수 역시 부울 연산자로 정의 가능하다. 이들 각각은 진리표를 통해 구분할 수 있으며, 경우에 따라 특별한 기호나 논리 연산으로도 나타낼 수 있다. 예를 들어, 배타적 논리합(XOR), 등가(Equal), NAND, NOR 등도 이 16개의 조합 안에 포함된다. 이러한 함수들은 일정한 규칙성을 가지며, 위 테이블에서는 이를 기반으로 각 연산에 대한 표현식을 정리하고 있다. 여기에 포함된 연산자는 상수 연산(0, 1), 단항 연산(보수, 전이), 그리고 이진 연산(NAND, NOR, XOR, IMPL, EQ 등)으로 구분된다.
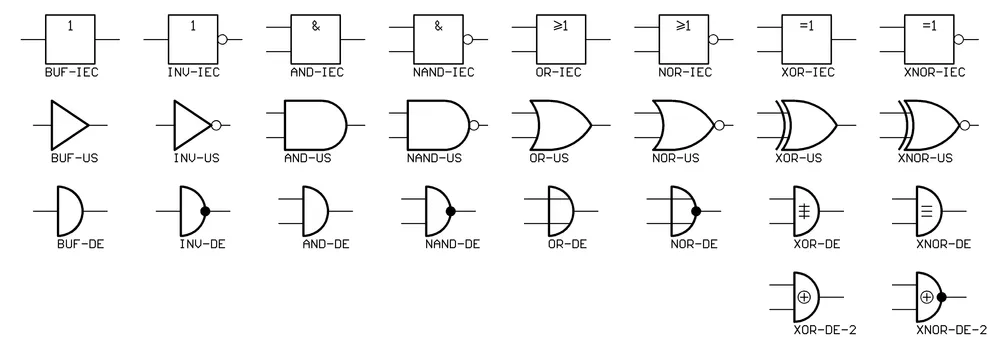
2.6 디지털 논리 게이트 및 집적 회로 (Digital Logic Gates and Integrated Circuits)
부울 함수는 기본적으로 AND, OR, NOT 연산으로 표현되므로, 실제 회로 구현에서는 이들 연산에 해당하는 논리 게이트(logic gate)를 사용한다. 16개의 부울 함수 중 일부는 상수값이거나 중복되기 때문에, 논리 회로 구현에 활용할 수 있는 실질적인 게이트는 10개 정도다. 그중에서도 NAND와 NOR는 가장 널리 쓰이는 표준 논리 게이트이다. 이들은 트랜지스터 회로로 쉽게 구현 가능하며, 어떤 부울 함수도 NAND나 NOR 게이트만으로 완전하게 표현할 수 있다는 특징이 있다.

이외에도 AND, OR, NOT, XOR, XNOR 등의 게이트가 사용되며, 각각의 게이트는 보통 한 개 또는 두 개의 입력을 가지고 하나의 출력을 생성한다. 그러나 NAND와 NOR 연산은 결합법칙(associative law)이 성립하지 않는다는 단점도 있다. 즉, (x ↓ y) ↓ z ≠ x ↓ (y ↓ z)와 같이 연산 순서에 따라 결과가 달라질 수 있다는 것이다. 이로 인해 여러 게이트를 연결하는 경우에는 연산 순서를 주의해서 설계해야 한다.
NAND와 NOR는 여러 개의 입력을 동시에 받을 수 있으며, 이 경우 각각 x ↑ y ↑ z = (xyz)’, x ↓ y ↓ z = (x + y + z)’의 형태로 나타난다. 이는 다중 입력 혹은 연속 연결된 게이트(cascaded gate)의 연산 결과를 보여주는 예시이다. XOR 연산자는 입력 변수 중 홀수 개가 1일 때 출력이 1이 되는 홀수 함수(odd function)이다. 세 개 입력이 주어지는 경우, 입력값들 중 홀수 개가 참일 때만 XOR 출력이 1이 된다. 또한, 긍정 논리(positive logic)와 부정 논리(negative logic) 시스템도 정의된다. 긍정 논리에서는 높은 전압(H)이 1, 낮은 전압(L)이 0을 의미하며, 부정 논리에서는 그 반대이다. 이 강의에서는 기본적으로 긍정 논리를 사용한다고 전제하고 설명한다.
논리 게이트는 개별 회로 부품으로 구현되기보다는 집적 회로(Integrated Circuits, ICs)의 형태로 사용된다. 집적 회로는 회로 내에 포함된 게이트의 수에 따라 네 가지 수준으로 분류된다:
- SSI (Small Scale Integration): 수십 개의 게이트 포함
- MSI (Medium Scale Integration): 수백 개 수준
- LSI (Large Scale Integration): 수천 개 수준
- VLSI (Very Large Scale Integration): 수만 개 이상의 게이트를 포함
집적 회로는 논리 패밀리(Logic Family)에 따라 다양한 방식으로 구현되며, 대표적인 논리군으로는 TTL (Transistor-Transistor Logic), ECL (Emitter Coupled Logic), MOS (Metal-Oxide Semiconductor), CMOS (Complementary MOS)가 있다. 이들은 각각 성능과 전력 소비, 구현 방식에 차이가 있다. 논리 회로를 설계할 때 고려해야 할 주요 파라미터로는 다음과 같은 요소들이 있다.
- Fan-out: 하나의 게이트 출력이 연결 가능한 다른 게이트 수
- Fan-in: 하나의 게이트가 수용할 수 있는 입력 수
- Power dissipation: 회로가 소모하는 전력량
- Propagation delay: 입력이 바뀐 후 출력이 바뀔 때까지 걸리는 시간
- Noise margin: 회로가 잡음을 견딜 수 있는 허용 범위
마지막으로, 복잡한 회로 설계를 위해 VLSI 설계에 특화된 컴퓨터 기반 도구(CAD)도 사용된다. 대표적인 구현 기술로는 ASIC(전용 집적회로), FPGA(현장 프로그래머블 게이트 어레이), PLD(프로그래머블 논리 장치), HDL(하드웨어 설명 언어) 등이 있으며, 이들을 통해 논리 회로를 자동화된 방식으로 설계하고 시뮬레이션할 수 있다.
'Computer Scinece > Computer Architecture & OS' 카테고리의 다른 글
| Digital Design [3] : 논리 회로 (Logical Circuit) (0) | 2025.04.16 |
|---|---|
| Digital Design [2] : 게이트 레벨 최소화 (Gate-Level Minimization) (0) | 2025.03.20 |
| Operating System [2]: 프로세스 (Processes) (1) | 2025.03.17 |
| Operating System [1]: 운영 체제 구조 (Operating System Structures) (0) | 2025.03.05 |