1. 순차회로
조합 논리 회로는 현재 입력만으로 출력을 결정하며, 기억 기능이 없다. 하지만 현실 세계에서는 입력의 순서나 과거 상태를 기억해야 하는 경우가 많다. 예를 들어, 비밀번호 입력기처럼 입력 순서를 기억해야 하는 장치가 이에 해당한다.
이러한 기능을 수행하기 위해 순차 회로가 사용된다. 순차 회로는 현재 입력과 이전 상태를 함께 고려하여 출력을 결정하는 회로이다. 즉, 기억 능력이 있는 회로이다.
순차 회로는 다음의 세 가지 요소로 구성된다.
- 조합 논리 회로: 입력과 현재 상태를 바탕으로 다음 상태와 출력을 계산한다.
- 기억 소자(Flip-Flop): 현재 상태를 저장한다.
- 피드백 경로: 저장된 상태가 다시 조합 논리 회로로 전달되어 다음 상태를 결정하는 데 사용된다.
언제 상태를 바꿀지, 즉 언제 생각을 바꿀지 정해주는 방식에는 동기식(Synchronous) 과 비동기식(Asynchronous) 이 있다.
동기식 회로
동기식 회로는 클럭이라는 기준 신호가 있을 때만 동작하는 회로이다. 여기서 클럭은 일정한 주기로 켜졌다 꺼지는 신호를 말한다. 이 신호는 마치 메트로놈처럼 리듬을 만들어주고, 회로는 이 리듬에 맞춰서만 상태를 바꾼다. 즉, 입력이 아무리 자주 바뀌더라도 클럭이 바뀌는 순간이 아니면 회로는 반응하지 않는다. 이런 방식은 예측 가능하고 안정적이다.
비동기식 회로
비동기식 회로는 클럭 신호 없이 입력의 변화에 즉시 반응하는 회로이다. 즉, 무언가 입력이 바뀌는 순간, 그 즉시 회로의 상태가 바뀐다. 클럭이라는 기준 없이 작동하기 때문에 속도는 빠를 수 있지만, 예상치 못한 동작이 발생하기도 쉽다. 데이터를 보낼 준비가 되었다는 신호가 들어오면 클럭 없이 바로 반응해서 데이터를 전송한다. 이런 방식은 속도가 빠르고 효율적이지만, 타이밍을 정확하게 맞추는 것이 어렵고, 동시에 여러 신호가 들어오면 회로가 혼란스러워질 수 있다.
2. 저장 소자 비교 – 래치와 플립플롭
저장 소자 : 디지털 회로에서 상태(0 또는 1)를 기억하는 장치를 저장 소자라고 한다. 입력이 없어도 현재 상태를 유지하고, 특정 조건이 되면 상태를 바꾼다. 대표적인 저장 소자는 래치(Latch)와 플립플롭(Flip-Flop)이다. 이 둘은 모두 1비트를 기억할 수 있으며, 주된 차이는 입력에 반응하는 방식이다.
2.1 래치

SR 래치는 디지털 회로에서 가장 기본적인 기억 장치 중 하나이다. 이 장치는 단 두 개의 입력만으로 1비트의 상태(0 또는 1)를 저장하고 유지할 수 있다. 래치는 클럭에 반응하는 것이 아니라, 입력 신호의 값 자체(level)에 반응한다. 즉, 입력이 1로 유지되는 동안 회로는 계속 반응할 수 있다. En(Enable) 같은 제어 신호가 1일 때에만 입력을 받아들이고, 0일 때는 상태를 유지한다. 이러한 구조는 비동기식 회로, 즉 클럭 없이 작동하는 회로에서 주로 사용된다.
2.1.1 SR 래치의 구조
SR 래치는 두 개의 논리 게이트(NOR 또는 NAND 게이트)를 서로 교차 연결해서 만든다. 이 구조는 출력 하나가 다른 게이트의 입력으로 다시 들어가는 피드백 구조로 되어 있어서, 한번 정해진 출력 상태를 계속 유지할 수 있다.
- S (Set): ‘1’을 설정하는 신호
- R (Reset): ‘0’을 설정하는 신호
2.1.2 SR 래치의 동작 방식

SR 래치에 S와 R 값을 다르게 주면 다음과 같이 작동한다:
- S = 1, R = 0 → Set 상태
→ Q는 1이 되고, Q’는 0이 된다
→ 회로는 “1”을 기억하게 된다 - S = 0, R = 1 → Reset 상태
→ Q는 0이 되고, Q’는 1이 된다
→ 회로는 “0”을 기억하게 된다 - S = 0, R = 0 → Hold 상태 (상태 유지)
→ 입력이 바뀌지 않았기 때문에 이전에 설정된 Q값을 그대로 유지한다
→ 예를 들어, 바로 전에 Set이 되었으면 계속 Q=1을 유지한다 - S = 1, R = 1 → 금지 상태 (Forbidden)
→ 두 출력 Q, Q’가 모두 0이 되어 논리적으로 모순이 발생한다
→ 이 상태는 정의되지 않으며, 회로 동작에 문제가 생길 수 있다
→ 그래서 실무에서는 이 상태가 나오지 않도록 주의해야 한다

NAND 게이트를 사용할 경우 동작은 NOR 래치와 반대로 동작한다.
- 기본 상태가 S = R = 1이며,
- S = 0, R = 1 → Set
- S = 1, R = 0 → Reset
- S = 1, R = 1 → 상태 유지
- S = 0, R = 0 → 금지 상태
이 구조는 입력이 0일 때 동작하기 때문에 Active-Low 입력이라고 부르며, SR 대신 S’R’ 래치라고 부르기도 한다.
2.1.3 Enable 신호를 갖는 SR 래치

SR 래치에 En(Enable)이라는 제어 신호를 추가해, 특정 상황에서만 입력 S와 R이 동작하도록 만든 형태이다. 즉, 회로가 아무 때나 반응하지 않도록 하고, 허락 신호(En = 1)가 있을 때만 작동한다. 입력을 통제할 수 있어서 조금 더 안정적인 설계가 가능하지만, 여전히 S=R=1 상황에서는 회로가 이상 동작할 수 있으므로, 주의가 필요하다.
2.1.4 D 래치 (Data Latch)

SR 래치의 단점(S=R=1 시 금지 상태 발생)을 해결하기 위해 만들어진 구조이다. 입력을 S와 R 두 개 대신 하나의 데이터 입력 D로 단순화했다. 동작은 Enable 신호가 켜져 있을 때만 입력 D를 받아들이고, 꺼지면 그 순간의 입력 상태를 기억하는 방식이다.
동작 원리
- En = 1 → 입력 D가 Q로 전달됨 (투과 상태)
- D = 1 → Q = 1 (Set)
- D = 0 → Q = 0 (Reset)
- En = 0 → Q는 마지막 입력 값을 계속 유지함 (기억 상태)
D 값이 그대로 Q로 복사되므로, 동작이 직관적이고 안정적이다. S=R=1 문제 자체가 발생하지 않도록 설계되어 있어 실무에서 매우 유용하다. 물탱크의 수위 센서를 예로 들자. D는 현재 수위 센서의 값이고, En은 센서가 측정을 허용할 때를 의미한다. En = 1일 때만 D 값을 읽어들이고, En = 0이면 그 값을 기억하고 유지한다. 이렇게 하면 측정 타이밍을 정확히 제어하면서도, 수위 값이 계속 바뀌어도 회로가 흔들리지 않는다.

2.2 플립 플롭
플립플롭은 래치와 달리 클럭 신호의 변화(edge) 에만 반응하여 상태를 변경하는 저장 소자이다.
래치는 입력 신호의 레벨(level) 에 따라 동작하므로 클럭이 1인 동안 계속해서 출력이 바뀔 수 있어 예측 불가능한 동작을 할 수 있다. 이러한 문제를 방지하기 위해, 플립플롭은 클럭의 에지(변화 순간) 에만 반응하도록 설계되어 있다.
즉, 클럭이 변화하는 순간에만 상태를 업데이트하고, 그 외 시간에는 출력을 유지하여 안정적인 동작을 보장한다.
2.1.1 트리거(Trigger)와 에지(Edge)
플립플롭은 입력 신호가 순간적으로 변화할 때만 동작하는데, 이 순간을 트리거라고 한다. 트리거는 보통 클럭 신호의 변화로 발생하며, 다음과 같은 두 가지 종류가 있다.

- Positive Edge (상승 에지): 클럭이 0에서 1로 변할 때 작동
- Negative Edge (하강 에지): 클럭이 1에서 0으로 변할 때 작동
플립플롭은 이 에지에만 반응하므로, 클럭이 지속적으로 1이거나 0인 경우에는 출력을 바꾸지 않다.
2.1.2 Master-Slave D 플립플롭
플립플롭은 일반적으로 두 개의 래치(Master와 Slave)와 하나의 인버터로 구성되며 Master-Slave 구성이라 불린다.
| Master 래치 | 입력을 잠깐 저장 | Clk = 1일 때 작동 |
| Slave 래치 | 출력을 내보냄 | Clk = 0일 때 작동 |

- Clk = 1 (클럭이 High): Master 래치가 활성화되어 입력 D 값을 저장한다. Slave는 비활성화 상태이며 출력은 변하지 않는다.
- Clk = 0 (클럭이 Low): Master는 비활성화되고, Slave가 활성화되어 Master가 저장한 값을 출력으로 전달한다.
즉, 실제 출력은 클럭이 1에서 0으로 떨어지는 하강 에지에서만 바뀌게 된다.

- 클럭 신호가 변화하는 순간에만 출력이 변하므로, 출력 변화가 일정하고 예측 가능하다.
- 입력이 바뀌더라도 클럭 에지가 아니면 출력에 영향을 주지 않아 노이즈에 강하고 안정적이다.
- 출력은 한 클럭 주기당 한 번만 갱신되므로, 동기식 회로에 적합하다.
2.1.3 D-type positive-edge triggered flip-flop (D형 상향 에지 트리거 플립플롭)
상향 에지 트리거 D 플립플롭이란 D(데이터) 입력을 받아, 클럭이 상승 엣지(0 → 1)가 되는 순간에만 출력 Q를 업데이트하는 회로이다.

이 플립플롭은 내부에 세 개의 SR 래치로 구성됩니다:
- 첫 번째 래치는 D 입력을 받아 저장한다.
- 두 번째 래치는 클럭(Clk)의 변화를 감지한다.
- 세 번째 래치는 최종 결과를 출력(Q)으로 보낸다.
이 구조는 클럭이 0에서 1로 바뀌는 딱 한 순간, D 값을 받아 Q에 반영하도록 설계되어 있다.

엣지 트리거 D 플립플롭이 정확히 동작하려면 세 가지 시간 조건을 만족해야 한다. Setup Time은 클럭 엣지 이전에 입력 D가 미리 안정되어 있어야 하는 시간이고, Hold Time은 클럭 엣지 이후에도 D를 잠시 더 유지해야 하는 시간이며, Propagation Delay는 클럭 엣지 이후 출력 Q가 최종 값으로 안정되기까지 걸리는 시간이다. 이 조건들이 지켜지지 않으면 회로는 잘못된 값을 저장하거나 출력이 흔들리는 등의 오류가 발생할 수 있으므로, 디지털 시스템의 신뢰성과 정확성을 위해 매우 중요하다.

2.1.4 JK 플립 플롭 & T 플립 플롭
JK 플립플롭은 디지털 회로에서 정보를 저장하거나 바꾸는 장치이다. 입력으로 J와 K라는 두 개의 신호를 받고, 클럭이 들어올 때 그 조합에 따라 출력(Q)을 바꾼다.
- J는 출력을 1로 만들고자 할 때 사용하는 입력이다.
- K는 출력을 0으로 만들고자 할 때 사용하는 입력이다.
- J와 K를 동시에 1로 만들면, 현재 출력 Q를 반전(toggle) 시킨다.
- 둘 다 0이면 아무 동작도 하지 않고 현재 상태를 유지한다.

| 0 | 0 | 상태 유지 (No Change) | Q는 이전 값을 그대로 유지 |
| 0 | 1 | 리셋 (Reset) | Q = 0 |
| 1 | 0 | 설정 (Set) | Q = 1 |
| 1 | 1 | 반전 (Toggle) | Q = Q' (출력 반전됨) |
JK 플립플롭은 다음의 수식으로도 표현된다:
D = JQ' + K'Q
이 식은 JK 플립플롭의 동작을 D 플립플롭으로 구현할 수 있음을 보여준다.
- J가 1이고 Q가 0이면: JQ' = 1 → D = 1 → Q는 1로 됨 (Set)
- K가 1이고 Q가 1이면: K' = 0 → K'Q = 0 → D는 0 → Q는 0으로 됨 (Reset)
- J = K = 1이면: D = Q' → 출력이 반전됨
- J = K = 0이면: D = Q → 출력 유지
T 플립 플롭은 입력이 하나만 있는 플립플롭으로, 입력 T의 값에 따라 출력 Q가 그대로 유지되거나 반전되는 동작을 한다. "T"는 Toggle(반전)을 의미한다.
→ T가 1이면 Q가 0이면 1로, 1이면 0으로 반전된다.
→ T가 0이면 아무 변화 없이 Q를 그대로 유지한다.

| 0 | 상태 유지 | Q = 이전 값 |
| 1 | 토글(반전) | Q = Q' (출력 반전됨) |
플립플롭은 D 플립플롭과 XOR 게이트 하나만으로도 만들 수 있다.
이때 입력 D는 다음과 같은 논리식을 따른다:
D = T ⊕ Q
⟶ 또는 논리식으로: D = T’Q + TQ’
이 식의 의미는 다음과 같다
- T가 0이면 D = Q → 상태 유지
- T가 1이면 D = Q' → 반전됨
즉, D 플립플롭의 입력 D를 현재 Q와 T의 XOR로 만들면
→ D 플립플롭이 T 플립플롭처럼 동작하게 된다.

| D 플립플롭 | Q(t+1) = D | 입력 D를 그대로 저장 |
| JK 플립플롭 | Q(t+1) = JQ' + K'Q | J, K 조합으로 Set/Reset/Toggle |
| T 플립플롭 | Q(t+1) = T ⊕ Q = TQ' + T'Q | T=1이면 반전, T=0이면 유지 |
- Preset: 출력 Q를 강제로 1로 설정 (클럭 무시)
- Clear (Reset): 출력 Q를 강제로 0으로 초기화 (클럭 무시)
- 용도: 전원 켠 후 초기 상태 설정에 사용
- Reset = 0 → 즉시 Q = 0
- Reset = 1 → 정상 클럭 동작 재개

2.3 Analysis of Clocked Sequential Circuits ( 클럭형 순차 회로 해석 )
순차회로의 동작은 입력, 현재 상태, 플립플롭의 출력에 따라 결정되며, 해석 과정에는 여러 단계가 포함된다.
- Logic Diagram: 회로도 (플립플롭 + 조합논리)
- State Equations: 상태 방정식 (다음 상태를 결정하는 식)
- State Table: 상태표 (입력, 현재 상태, 다음 상태, 출력 정리)
- State Diagram (optional): 상태도 (상태 전이 시각화)

회로 정보
- D 플립플롭 2개: A, B
- 입력: x
상태 방정식
- A(t+1) = A·x + B·x
- B(t+1) = A'·x
출력식
- y = (A + B)·x'
상태는 A와 B로 표현되며, 출력은 현재 상태와 입력의 조합에 따라 결정된다.
진리표

- Present State: 현재 상태 (예: A, B 값)
- Input: 외부 입력 (예: x)
- Next State: 다음 상태 (A(t+1), B(t+1))
- Output: 출력 y
행 수
- m개의 플립플롭 + n개의 입력 → 총 2^(m+n)개의 조합 (행)
상태도 (State Diagram)

- 각 상태는 플립플롭 값으로 표시 (예: A=0, B=1 → 상태 01)
- 전이선은 입력/출력으로 라벨링됨 (예: x/y)
- 전이는 클럭 엣지에서 발생하며 입력 조건에 따라 다음 상태로 넘어감

D 플립플롭 기반 순차 회로는 플립플롭과 조합 논리로 구성되며, 플립플롭 입력은 불 대수식으로 표현된다. 예를 들어, 입력식이 DA = Ax + Bx, DB = A'·x인 경우, 각 플립플롭의 다음 상태는 현재 상태(A, B)와 입력(x)에 의해 결정된다. 출력도 y = (A + B)x’처럼 상태와 입력의 조합으로 표현된다.
JK 플립플롭 기반 순차 논리 회로 해석
회로 해석은 논리 다이어그램을 그리고, 상태표를 작성한 뒤, 상태도(State Diagram)를 통해 시각적으로 상태 전이를 표현하는 방식으로 이루어진다. XOR 논리가 포함된 식(예: DA = A ⊕ x ⊕ y)도 마찬가지로 해석되며, 모든 경우의 조합에 대해 다음 상태와 출력을 도출한다. 이 방식은 순차 회로의 동작을 체계적으로 분석하고 설계하는 데 필수적이다.
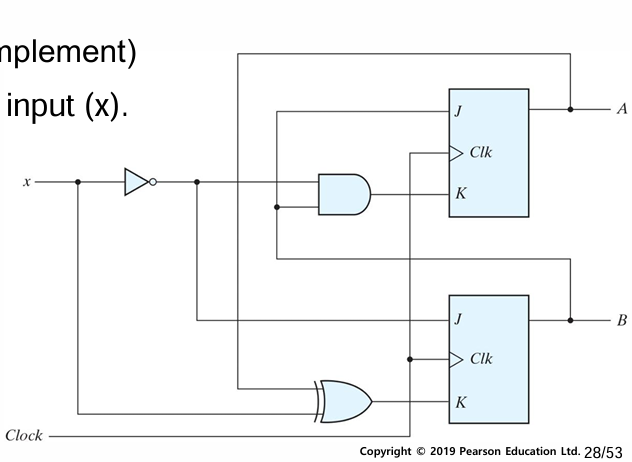
이 회로는 두 개의 JK 플립플롭(A, B)과 하나의 입력(x)으로 구성된 순차 회로이다. 회로 해석을 위해 먼저 각 플립플롭의 입력 논리식을 정의한다.
- A 플립플롭: JA = B, KA = B·x’
- B 플립플롭: JB = x’, KB = A ⊕ x
그 다음, 각 입력 조합(A, B, x)에 대해 JA, KA, JB, KB의 값을 구하고, JK 플립플롭의 특성표에 따라 다음 상태 Q(t+1)을 결정한다. 특성표는 다음과 같다:
- J = 0, K = 0 → 상태 유지
- J = 1, K = 0 → 1로 설정(Set)
- J = 0, K = 1 → 0으로 리셋(Reset)
- J = 1, K = 1 → 반전(Toggle)
이러한 과정을 바탕으로 상태표를 작성하고, 현재 상태(AB), 입력(x), 다음 상태(AB)’를 모두 정리할 수 있다. 이후, 이를 바탕으로 상태도(State Diagram)를 작성하면, 입력 x에 따른 상태 전이 흐름을 시각적으로 파악할 수 있다. 이와 같은 해석 방법은 JK 플립플롭을 사용하는 순차 회로의 동작을 체계적으로 분석하는 데 사용된다.
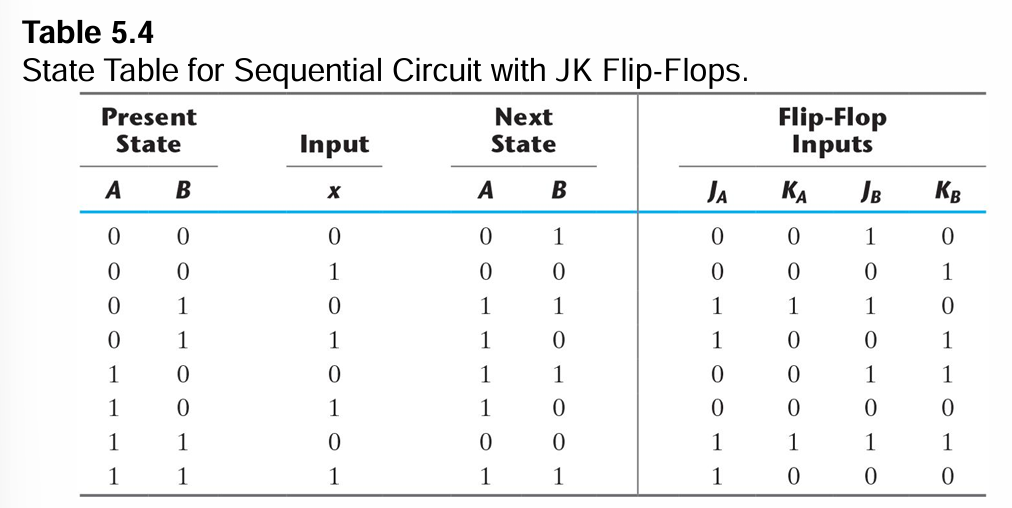
- 현재 상태 (Present State): A, B
- 입력 (Input): x
- 플립플롭 입력 (for help): JA, KA, JB, KB
- 다음 상태 (Next State): A(t+1), B(t+1)
다음 상태 계산 (Characteristic Equations 이용)
각 플립플롭의 다음 상태는 입력 논리식과 특성식을 조합하여 다음과 같이 계산된다.
🔹 A(t+1):
A(t+1) = JA′ + K′A
= B·A′ + (B·x′)'·A
= A′B + AB′ + A·x
→ 이 식은 J, K의 조합 논리를 대입한 후 불 대수로 정리한 결과이다.
🔹 B(t+1):
B(t+1) = JB′ + K′B
= x′·B′ + (A ⊕ x)'·B
= B′x′ + AB·x + A′B·x′
→ 역시 JK 특성식에 입력식을 대입해 전개한 것이다.
해석 요약
- 각 플립플롭의 J, K 입력식을 먼저 대입하고,
- 그다음 특성식(Q(t+1) = JQ' + K'Q)을 이용해
- 다음 상태 식을 불 대수로 유도한다.
이러한 식을 바탕으로 상태표를 완성하고, 상태도의 상태 전이도 도출할 수 있다.
JK 플립플롭은 입력이 복잡할 수 있지만, 특성식을 통해 모든 상태 전이를 명확하게 정의할 수 있다는 장점이 있다.

T 플립플롭 기반 순차 회로 해석
이 회로는 T 플립플롭 2개(A, B)와 입력 x로 구성되며, 이진 카운터(binary counter)로 동작한다.
각 플립플롭의 다음 상태는 T 플립플롭의 특성식과 입력식을 바탕으로 결정된다.

특성식 (Characteristic Equation)
Q(t+1) = T ⊕ Q = T’Q + TQ’
입력 T가 1이면 현재 상태 Q를 반전시키고,
T가 0이면 현재 상태를 그대로 유지한다.
플립플롭 입력식 (Input Equations)
- TA = B·x
- TB = x
입력 x에 따라 T값이 결정되고, 이에 따라 A, B 플립플롭의 상태가 변화한다.
출력식 (Output Equation)
- y = A·B
출력은 두 플립플롭의 상태 A와 B가 모두 1일 때 1이 된다.
동작 요약
- x = 1일 때: 회로는 2비트 이진 카운터처럼 동작
- 상태가 00 → 01 → 10 → 11 → 00 순으로 전이됨
- x = 0일 때: TA = 0, TB = 0이 되므로
- 두 플립플롭 모두 상태 유지 → 현재 상태 고정
T 플립플롭 회로의 다음 상태 계산
회로는 T 플립플롭 A와 B, 그리고 입력 x로 구성된다.
앞서 주어진 T 입력식을 특성식에 대입하면, 다음과 같은 다음 상태 방정식이 도출된다.

T 플립플롭의 기본 특성식은 다음과 같다:
Q(t+1) = T ⊕ Q
이 특성식에 각 플립플롭의 입력 T를 대입하면:
- TA = B·x
- TB = x
- A(t+1) = A ⊕ (B·x)
→ 불 대수 전개 결과:
A(t+1) = A·B’ + A·x’ + A’·B·x - B(t+1) = B ⊕ x
→ 그대로 유지됨
이렇게 계산된 식은 현재 상태(A, B)와 입력 x에 따라 다음 상태(A’, B’)가 어떻게 바뀌는지를 명확히 보여준다.

이 상태 방정식은 현재 상태(A, B)와 입력(x)에 따라 다음 상태(A’, B’)를 계산하는 데 사용된다. 특히 B(t+1)은 매우 단순하게 입력 x와 B의 XOR로 결정되므로, x=1일 때는 B가 반전되고, x=0일 때는 B가 유지된다. A(t+1)은 보다 복잡한 불 대수식으로 표현되며, 여러 조건의 조합에 따라 상태가 전이된다.
이러한 방정식을 기반으로 Table 5.5의 상태표가 작성되며, 모든 가능한 A, B, x 조합에 대해 A’, B’가 계산되고 기록된다. 이를 통해 회로의 동작을 체계적으로 분석하고 상태 전이 흐름을 파악할 수 있다.
이 회로는 두 개의 T 플립플롭(A, B)으로 구성된 순차 회로로, 입력 x의 값에 따라 **상태 전이 방식이 달라지는 이진 카운터(binary counter)처럼 동작한다. 입력 x가 1일 때, 회로는 매 클럭마다 상태가 순서대로 전이되며, 00 → 01 → 10 → 11 → 00의 2비트 카운팅 순서를 따른다. 반면, x가 0이면 TA = TB = 0이 되어 두 플립플롭 모두 상태를 유지하므로, 회로는 현재 상태를 고정하고 아무런 전이가 발생하지 않는다. 이처럼 입력 x를 통해 카운팅 동작과 정지 상태를 제어할 수 있는 단순한 제어형 카운터 회로로 동작한다.

순차 회로는 입력, 출력, 내부 상태를 가지고 동작하며, 이를 체계적으로 표현하기 위해 유한 상태 기계(FSM, Finite State Machine) 모델이 사용된다. FSM에는 두 가지 주요 형태가 있으며, 각각 Mealy 머신과 Moore 머신이다. Mealy 머신은 출력이 현재 상태와 입력에 의해 결정되고, Moore 머신은 출력이 현재 상태만으로 결정된다. 하나의 회로가 이 두 방식의 출력을 동시에 가질 수도 있으며, FSM은 순차 회로의 동작을 설계하고 분석하는 데 있어 가장 널리 사용되는 모델이다.
상태 축소와 할당
상태 축소와 할당 (State Reduction and Assignment)
- 분석(Analysis): 이미 만들어진 회로를 해석
→ 회로도 → 상태표 → 상태도 - 설계(Design): 명세를 바탕으로 회로를 만드는 과정
→ 요구사항 → 논리 회로
상태 축소는 입력과 출력 동작이 완전히 같은 상태들을 하나로 합치는 과정이다.이렇게 하면 상태 수가 줄어들어 회로가 더 간단해질 수 있다. → 플립플롭 수와 논리 게이트가 줄어들 수도 있다, 하지만 항상 그런 것은 아니다.
어떤 상태들이 합쳐질 수 있을까?→ Equivalent States (동등한 상태)
두 상태가 같은 입력에 대해 같은 출력을 내고, 같은 또는 동등한 다음 상태로 이동한다면, 그 둘은 동등한 상태이다. 이런 상태들은 기능적으로 완전히 똑같으므로, 하나로 합쳐도 회로 동작에는 영향이 없다.

상태 축소는 상태도 또는 상태표를 기반으로, 기능이 완전히 같은 상태들을 하나로 합치는 과정이다.
- 상태도에서 상태표 유도
먼저, 상태도의 상태 전이와 출력을 기반으로 상태표(state table)를 작성한다. - 동등한 상태 찾기
상태표를 보면, 어떤 상태들이 입력에 대해 같은 출력과 같은 다음 상태를 가지는지 확인할 수 있다.
예시에서는 다음과 같이 동등한 상태(Equivalent States)를 찾았다:- 상태 e와 g는 동작이 완전히 같으므로 하나로 합칠 수 있다.
- 상태 f와 d도 마찬가지로 동등하므로 병합 가능하다.
- 상태 병합 결과
원래 7개의 상태가 있었지만, e↔g, f↔d를 각각 병합하여 5개의 상태만으로 회로를 표현할 수 있게 된다.

이 과정을 통해 전체 회로의 복잡도는 줄이고, 출력 동작은 기존과 완전히 동일한 회로를 만들 수 있게 된다.
즉, 기능은 그대로 유지하면서도 회로가 더 단순해지는 최적화가 이루어지는 것이다.
상태 축소를 통해 동등한 상태들을 병합한 뒤 작성한 새로운 상태도를 **Reduced State Diagram(축소된 상태도)**라고 한다.
원래 상태도(Fig. 5.25)에는 7개의 상태가 있었지만, 상태 분석 결과:
- 상태 g는 e와 동등
- 상태 f는 d와 동등
이라는 사실이 밝혀졌다.
따라서 g를 e로, f를 d로 대체하면 출력과 상태 전이 모두 동일하게 유지된다.

이렇게 상태를 병합해 만든 축소 상태도(Fig. 5.26)는, 입력 시퀀스나 출력 결과가 원래 상태도와 완전히 동일하다.
즉, 동작은 같지만 상태 수는 더 적은, 더 효율적인 설계가 된 것이다.

상태 할당이란, 각 상태에 고유한 이진 코드(binary code)를 부여하는 과정이다. 이는 상태를 플립플롭으로 표현하기 위해 필수적인 단계이다.
- 상태가 m개라면, 그것들을 구분하기 위해 최소 n비트의 이진 코드가 필요하다.
- 이는 수학적으로 2ⁿ ≥ m을 만족해야 한다.
- 5개 상태 → 최소 3비트 필요 (2³ = 8 ≥ 5)
사용되지 않는 상태 = Don’t-Care
- m개의 상태 중 **나머지 코드(2ⁿ - m)**는 사용되지 않게 된다.
- 이런 미사용 상태는 “don’t-care”로 간주되며,
회로 최적화 시 유연성을 높여 더 단순한 논리식 도출에 도움을 줄 수 있다.
하지만 상태 수가 줄어든다고 해서 항상 회로가 더 단순해지는 것은 아니며,
논리식 구조나 상태 전이 복잡도에 따라 다를 수 있다.
| Binary Encoding | 상태마다 2진수 순서대로 코드 할당 (예: 000, 001, 010...) |
| Gray Code | 인접 상태 간 1비트만 바뀜 → 카노 맵 최적화에 유리 |
| One-Hot Encoding | 상태 수만큼 플립플롭 사용, 단 한 비트만 1 → 논리 회로 단순화, FPGA에 적합 |

상태 할당 방식 (State Assignment Methods)
상태 축소가 끝난 뒤, 각 상태에 **이진 코드(상태 코드)**를 부여해야 실제 회로로 구현할 수 있다. 이때 사용할 수 있는 대표적인 상태 인코딩 방식은 다음 세 가지이다.
1. Binary Encoding (이진 인코딩)
- 상태에 순차적인 이진수 코드를 부여한다.
- 예를 들어, 상태가 5개이면:
S0 = 000, S1 = 001, S2 = 010, S3 = 011, S4 = 100 - 장점: 비트 수가 적고, 플립플롭 수도 가장 적게 든다.
- 단점: 다음 상태 계산 논리가 복잡할 수 있다.
2. Gray Code (그레이 코드)
- 상태 간 전이가 일어날 때 단 하나의 비트만 바뀌도록 상태 코드를 배치한다.
- 예: S0 = 000, S1 = 001, S2 = 011, S3 = 010, S4 = 110
- 장점: 카노 맵을 사용할 때 논리식 최적화에 유리하다.
- 단점: 상태 수가 많아지면 설계 복잡도는 여전히 존재
3. One-Hot Encoding (원-핫 인코딩)
- 상태 수만큼 플립플롭을 만들고,
각 상태를 오직 하나의 플립플롭만 1이 되도록 할당한다.
나머지는 모두 0이다. - 예: S0 = 00001, S1 = 00010, S2 = 00100, S3 = 01000, S4 = 10000
- 장점: 다음 상태 논리와 출력 논리가 매우 단순해진다.
- FPGA 설계에 특히 유리하다.
- 단점: 상태 수가 많아지면 플립플롭이 많이 필요하다.
Deisgn Procedure
순차 회로 설계는 **요구사항(명세)**에서 출발해 논리 회로도 또는 불 함수로 구현하는 전체 과정을 말한다.
특히 D 플립플롭이 가장 널리 사용되며, JK나 T 플립플롭도 D 플립플롭과 조합 논리로 대체 가능하다.
🔹 기본 설계 단계
- 문제 정의: 회로가 해야 할 동작을 서술형으로 설명
- 상태도 작성: 상태 간 전이를 그림으로 표현
- 상태 축소: 동등한 상태가 있다면 병합
- 상태 할당: 상태에 이진 코드 부여
- 상태표 생성: 현재 상태, 입력 → 다음 상태 및 출력 정리
- 플립플롭 종류 선택: 주로 D 플립플롭 사용
- 입력/출력 논리식 도출: 불 식 또는 카노 맵으로 정리
- 논리 회로도 작성: 게이트와 플립플롭을 이용해 회로 구현

🔹 예제: 연속된 1이 세 개 이상 나올 때 검출하는 회로 (Sequence Detector)
- 목표: 입력 x에 대해 "111" 이상이 들어오면 출력 y = 1
- 모델: Moore 머신 사용 → 출력은 상태에만 의존
상태도 구성:
- S0: 초기 상태
- S1: 1이 한 번 입력됨
- S2: 연속된 1이 두 번
- S3: 연속된 1이 세 번 이상 → 이 상태에 머무름

🔹 회로 구성: D 플립플롭 2개 사용 (A, B로 4개 상태 표현)
- 입력: x
- 상태: A, B (플립플롭 출력)
- 출력: y = AB
- 다음 상태 함수 (from 카노 맵):
- DA = A·x + B·x
- DB = A·x + B'·x
➡️ D 플립플롭의 특성상, Q(t+1) = D이므로 다음 상태식을 바로 D 입력으로 사용 가능하다.


🔹 JK 플립플롭 사용 시
- D 플립플롭과 달리, **JK는 입력이 2개(J, K)**이므로
→ 상태표와 **JK 플립플롭 자극표(Excitation Table)**를 사용해 J와 K 입력식을 유도해야 함. - 설계 과정:
- 상태표에서 현재 상태와 다음 상태 비교
- Excitation Table로부터 필요한 J, K 값을 찾음
- J와 K의 진리표 작성
- 카노 맵으로 논리식 단순화
➡️ JK는 복잡하지만 논리 최적화에 유리할 수 있다.
🔹 T 플립플롭으로 카운터 설계
- 3비트 이진 카운터 예시: 000 → 001 → 010 → ... → 111 → 000
- T 플립플롭은 입력 T가 1일 때 Q가 반전되므로, 카운터 회로에 적합
- 설계 순서:
- 상태표 작성 (현재 상태 → 다음 상태)
- T 플립플롭의 자극표 사용
- 각 T 입력에 대한 카노 맵 작성
- 논리식 도출 → 회로도 완성






