
1 - The Essence of Linear Algebra
Based on the lecture by 3B1B Youtue, Professor Seunkyu Lee
선형대수학을 전공기초 수업을 통해 배우기는 했지만 가우스 소거법, 크라메르 법칙같은 계산법과 문제 풀이에만 치중했을 뿐 행렬곱이 어떻게 정의되는지, 고윳값의 의미는 무엇인지 수학적인 본질은 이해하지 못했다. 후에 책과 유튜브를 통해 선형대수에 대해 다시 공부하면서, 선형대수는 수로써의 연산 뿐만 아니라 기하학 수준에서 이해하는 것이 매우 중요하다는 것을 알게 되었다.
공간이라고 생각하면 직관이 먹힌다
프로그래머를 위한 선형대수 - 히라오카 카즈유키 저
선형대수를 시각화하여 이해하는 것은 그 본질을 파악함에 있어 유용한 방법이다. 따라서 Ruby로 직접 시각화하거나 영상 강의를 시청하는 것을 추천한다.
1. 벡터
벡터, 스칼라, 선형 결합, 기저, 선형 독립
벡터(Vector) : 벡터는 크기와 방향을 가진 수학적 대상으로, 어디로 얼마나 이동하는 지를 나타낸다.
- 수학적 관점에서 벡터는 머리가 꼬리(원점)으로부터 얼마나 떨어져 있느냐를 나타낸다. 즉, 원점에 고정되어있는 화살표를 떠올리면 된다.
벡터의 덧셈 : 한 벡터를 움직여서 다른 벡터의 머리에 오도록 놓는다. 이제 벡터의 꼬리로부터 움직인 벡터의 머리를 이어 새로운 벡터를 그려주면 그 벡터가 두 벡터의 합이다. 이것이 왜 타당한가? 그것은 수직선 위의 숫자를 더하는 과정을 생각해보면 된다. 2 + 5를 수직선에 나타내면 오른쪽으로 두 칸, 그리고 다섯 칸을 이동하여 총 일곱 칸을 이동한 것인데 2차원 벡터의 수직 방향과 수평 방향으로 재해석 한 뒤 같은 원리를 적용하면 된다.
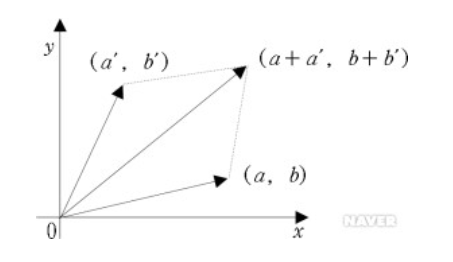
벡터의 덧셈
벡터의 스칼라배(Scalar) : 벡터 v 에 스칼라(실수) k 를 곱하면 k * v 라는 새로운 벡터를 얻는다. 이 새로운 벡터를 벡터 v 의 스칼라배라고 한다.
- 배열로서의 관점에서 벡터의 각 항에 스칼라를 곱하면 스칼라배를 얻을 수 있다.
- 벡터의 스칼라배는 벡터의 크기를 k배만큼 스케일링 하는 것으로 기하학적 의미를 갖는다.
선형대수를 공부하면서 이 숫자 쌍과 2차원 벡터 사이의 상호작용을 항상 염두해두자
단위 벡터 : 크기가 1인 벡터를 말한다. 즉, 방향만 가지고 있고 크기는 1로 고정되어 있다.
이제 [3,-2] 라는 벡터의 각 좌표를 단위 벡터의 스칼라라고 생각해보자. 이런 의미에서, 좌표쌍이 나타내는 벡터는 두 스케일된 벡터의 합이 된다. 즉, 이는 벡터를 스케일된 두 벡터의 합으로 보는 발상이다. 이 발상은 이후 여러 변환의 직관적 해석에 있어 중요하니 잘 기억해두자.
3차원 공간 기저(wikipedia)
선형 결합(Linear Combination) : 벡터의 선형결합은 벡터에 스칼라를 곱하고 더하여 새로운 벡터를 만드는 연산이다.
기저(Basis) : 벡터 공간 V의 기저는 V의 모든 벡터를 선형 결합으로 유일하게 표현할 수 있는 벡터들의 집합이다. 쉽게 말하면, 기저는 벡터 공간의 모든 벡터를 만들 수 있는 기본 벡터들의 집합인 것이다.
- 위에 벡터를 스케일된 두 벡터의 합으로 보는 발상으로 보면 단위 벡터가 아닌 다른 어떤 벡터라도 두 스칼라를 택해 각 벡터를 스케일 한 뒤 더했을 때 모든 2차원 벡터를 만들 수 있다는 걸 알 수있다.
Span (wikipedia)
생성(Span) : 벡터 공간 V에서 벡터들의 집합 S가 V의 모든 벡터를 유한 선형 결합으로 표현할 수 있다면 S는 V의 부분 공간이며, S는 V에서 벡터들의 선형 생성이라고 한다. 쉽게 말해, 벡터들의 집합 S가 V의 모든 벡터를 만드는 데 필요한 최소한의 벡터들을 가지고 있다는 의미이다.
- 즉 선형생성이란 벡터의 덧셈과 스칼라배, 이 두 기초 연산만 가지고 다다를 수 있는 모든 가능한 벡터들엔 무엇이 있는가? 라고 묻는 것과 같다.
- 대부분의 벡터의 쌍은 결국 무한한 2차원 평면 전체를 생성하기에 이르지만 둘이 일직선 위에 있다면 그들의 생성은 단지 직선이다.
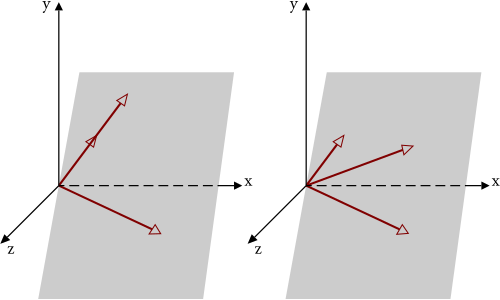
(좌) 선형 독립 (우) 선형 종속 (wikipeia)
이 기하학적인 원칙을 생각하면 선형 종속과 선형 독립의 개념도 쉽게 이해할 수 있다. 두 이차원 벡터가 선형종속의 관계에 있다면, 그들의 생성은 단지 직선일 뿐인 것이다.
선형 종속 (Linearly Dependent) : 벡터 공간 V에서 벡터들의 집합 S가 어떤 벡터를 다른 벡터들의 선형 결합으로 표현할 수 있다면 S는 선형 종속이라고 한다. 쉽게 말하면, 벡터들의 집합 S에서 어떤 벡터를 다른 벡터들로 만들어낼 수 있다는 의미이다.
선형 독립 (Linearly Independent) : 벡터 공간 V에서 벡터들의 집합 S가 어떤 벡터도 다른 벡터들의 선형 결합으로 표현될 수 없다면 S는 선형 독립이라고 한다. 쉽게 말하면, 벡터들의 집합 S에서 어떤 벡터도 다른 벡터들로 만들어낼 수 없다는 의미이다.
2. 행렬과 선형 변환의 관계
선형 변환(Linear Transformation) : 형 변환은 벡터 공간 V의 벡터를 벡터 공간 W의 벡터로 변환하는 함수이며, 벡터 덧셈과 스칼라 배수 연산을 보존한다는 의미이다.
- 그렇다면 함수와 역할이 동일한데, 왜 선형 변환이라는 용어를 사용하는가? 이것은 단어가 입출력 관계의 특정 시각화 방식을 내포하기 때문이다. 앞으로 이 선형 변환을 움직임이라고 생각해보자.
- 일반적인 좌표계를 격자선이 평행하고 균등한 상태를 유지한 상태에서 행렬에 따라 변환하고, 이 변환된 좌표계에서 앞서 설명한 벡터를 스케일된 두 벡터의 합으로 보는 관점을 적용하면 도달점을 유추할 수 있다.
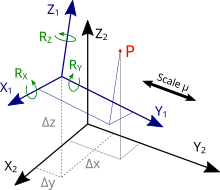
3차원 공간의 변환 (wikipedia)
아무 의미부여도 없이 암기만 했던 행렬 곱 공식을 이러한 기하학적인 움직임을 염두해둔다면 벡터와 행렬의 곱이 어떻게 정의된 것인지 직관적으로 이해할 수 있다. 이를 확장시키면, 행렬의 곱까지 일맥상통하게 파악할 수 있는 것이다. \
요약 : 선형 변환은 공간이 움직이는 방식 중 하나로 격자선이 평행하고 균등한 상태를 유지하면서 원점은 고정되어 있는 것을 만족하는 변환이다. 선형 변환은 숫자 몇 개를 가지고 기술 가능하며 이들은 기저 벡터가 도달하는 정보를 포함한다. 행렬은 이 변환들을 기술하기 위한 도구이며 각 열이 기저벡터의 도달 좌표이다. 행렬 벡터의 곱셈은 변환에 의한 새로운 벡터를 계산하는 방법이다. 행렬을 볼 때마다 일종의 공간 변환으로도 해석해보자.
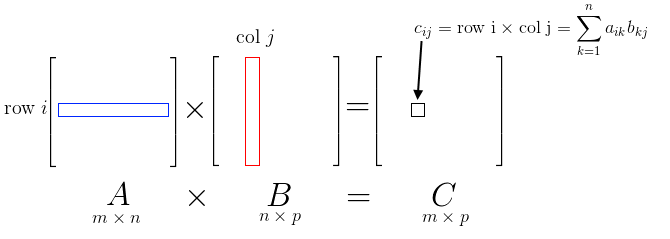
행렬의 곱을 구하는 공식 (wikipedia)
선형 변환의 합성 : 두 벡터 공간 V, W, Z 사이의 선형 변환 T : V → W와 U : W → Z가 있을 때, U ∘ T : V → Z를 선형 변환의 합성이라고 한다. 쉽게 말하면, 먼저 T를 적용한 후 U를 적용하는 것과 같다.
- 직관적으로 이해하기 위해선, 회전 변환을 하는 행렬과 전단 변환을 하는 행렬의 합성을 기저벡터에서 시작해 순차적으로 적용해본다 생각하면 편하다.
- 이를 기반으로 상단의 N차원 행렬곱의 연산 과정을 유추해보자. 선형변환에서 정리한대로 행렬 B의 J 번째 벡터에 행렬 A를 적용하려면 j(hat)에 행렬A를 곱해주면 된다. 이렇게 행렬 C의 j번째 열을 구할 수 있고 모든 j 벡터의 집합이 행렬 C가 된다.
- 그렇다면 A와 B의 순서를 바꾸더라도 결과가 같을까? 이 역시도 회전 변환과 전단 변환의 기하학적 움직임을 연상해본다면 쉽게 답을 유추할 수 있다. 회전 후 전단하는 것과 전단 후 변환하는 것은 확연한 차이가 생긴다.
3. 행렬식
3. 행렬식
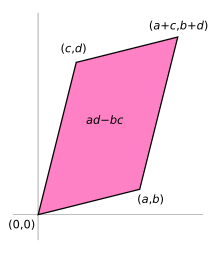
A determinant of a 2-dimensional matrix and a 3-dimensional matrix (Wikipedia)
정방 행렬 : 정방 행렬은 행과 열의 개수가 같은 행렬이다.
행렬식(Determinant) : 행렬식은 정방 행렬에 하나의 숫자를 대응시키는 함수이다.
- 선형변환을 보다보면 몇몇은 공간을 넓히는 것 같고 몇몇은 공간을 찌그러뜨리는 것 같다는 직관을 받을 수 있다. 이러한 선형 변환을 이해할 때 유용한 방법 중 하나는 그것이 넓어지거나 찌그러지는 정도를 실제로 재는 것이다. 단위 정사각형의 넓이가 변화하는 정도를 알면 가능한 모든 영역의 넓이 변화를 파악할 수 있다. 선형 변환으로 인해 어떤 스케일 인자만큼 넓이에 변화가 있을 떄 이 인자가 바로 그 변환의 행렬식인 것이다.
- 어떤 2차원 변환의 행렬식이 0이라면 변환은 공간 전체를 직선 또는 한 점으로 찌그러뜨린다. 즉 어떤 영역의 넓이든 0이 돼 버리는 것이다. 따라서 행렬식을 통해 해당 행렬에 해당하는 변환이 차원 자체를 낮추는지 여부를 계산할 수 있고 이를 통해 역행렬의 존재 여부와 연립방정식의 해 존재 여부를 파악할 수 있는 것이다.
- 2 * 2 행렬의 행렬식은 ad-bc인데, 평행사변형의 넓이를 유도하다보면 일반화해볼 수 있다.
4. 역행렬
역행렬(Inverse Matrix) : 역행렬은 행렬 곱셈에 대한 역원 역할을 하는 행렬이다. 즉, A라는 행렬의 역행렬을 A^(-1)이라고 표기할 때, AA^(-1) = A^(-1)A = I (단위행렬)가 성립한다. 역행렬이 존재하는 행렬을 가역행렬 이라고 하며 행렬식이 0이 아닌 경우에만 역행렬이 존재한다.
- 기하적 관점에서 결국 AA^(-1)는 아무것도 하지 않는 변환이고 이를 항등변환이라고 한다.
- 변환 A가 공간을 하위 차원으로 찌그러뜨리면,예를 들어 2차원 공간에서 변환된 직선은 평면으로 되돌릴 수 없다. 직선을 펼치려면 개별 벡터마다 벡터로 가득 찬 직선으로 변환해야하는데 함수는 단일 입력에 대해 단일 출력만 취할 수 있기 때문이다. 하지만 역이 없을 때에도 해는 존재할 수 있다. 변환이 공간을 직선으로 변환시켰을 경우 운좋게도 벡터 v가 직선 위에 있다면 해는 존재한다. 그리고 3차원 행렬의 예시를 생각할 때 평면으로 찌그러뜨릴 때보다 직선으로 찌그러질 때 해는 훨씬 더 제한적으로 존재한다. 이것을 랭크로 표현할 수 있다.
Rank from row echelon forms (wikipedia)
랭크(Rank) : 행렬이 나타낼 수 있는 독립적인 벡터의 최대 개수를 의미한다. 즉, 행렬의 행 또는 열 중 서로 선형 독립인 벡터의 최대 개수이다.
- 변환 후 출력이 직선, 즉 1차원일 때는 랭크 1
5. 내적과 외적
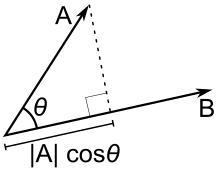
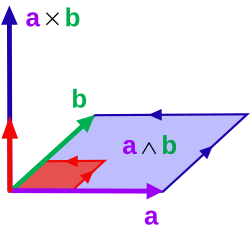
내적(좌)과 외적(우)
내적(Dot Product)
외적(outer product)
6. 고유값

7. 기하 공간
Geometric objects
1. Spaces
기존의 벡터 공간에서는 점의 위치는 기술할 수 없다. 수학적으로 이러한 좌표계는 아핀 공간, 유클리드 공간이라는 개념으로 다룰 수 있다.
벡터 공간 (Vector Space)
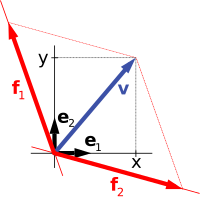
Vector Space
벡터 공간만으로는 점의 절대적인 위치를 나타내기 어렵다. 왜냐하면 벡터 공간 자체에는 기준점(원점)의 개념이 없기 때문이다.
존재가능한 요소 : Scalar, Vector
가능한 연산 : 벡터-벡터 합, 벡터-스칼라 배
아핀 공간 (Affine Space)
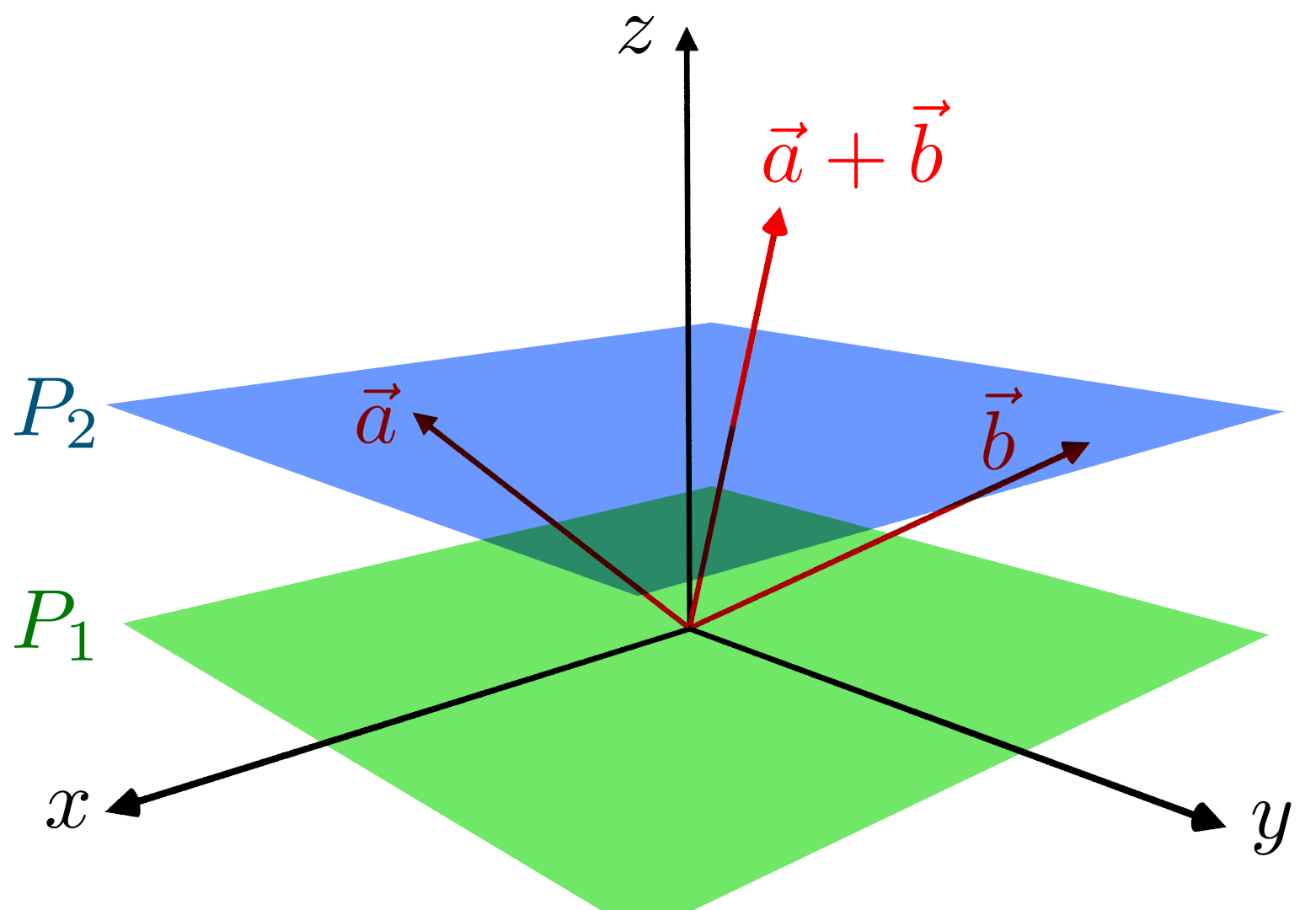
Affine Space
아핀 공간은 벡터 공간을 기반으로 하지만, 점 (point) 개념을 추가하여 상대적인 위치 관계를 나타내는 구조이다.
존재가능한 요소 : Scalar, Vector, Point
가능한 연산 : 벡터-벡터 합, 벡터-스칼라 배, 벡터-점 합, 점-점 빼기
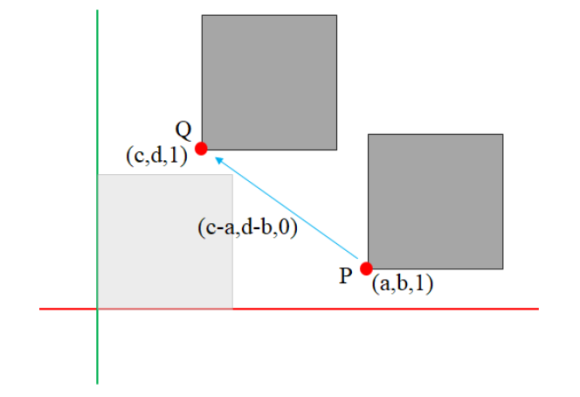
기저 벡터가 만든 벡터 공간을 (a, b)와 (c,d)만큼 이동시킨 두 개의 공간이 있다고 가정하자. 그러면 이동 행렬에서 살펴본 것처럼 이동 행렬로 만들어진 새로운 공간의 원점 P의 좌표는 (a,b,1)이고 원점 Q의 좌표는 (c,d,1)이 된다. 이 원점 좌표가 아핀 공간의 점(point)이다. 그리고 (a,b)에서 시작하는 원점이 (c,d)로 옮겨지려면 (c-a, d-b)만큼 옮겨져야 하는데 z값은 1을 유지해야 이동에 의한 선형 변환을 유지할 수 있게 된다. 그래서 이를 만족하는 값은 (c-a, d-b, 0)이 된다.
이로서 알 수 있는 것은 점은 세 번째 성분을 1로 표시하고 벡터는 0으로 표시된다는 것이다. 실제로 아핀 공간에서 점과 벡터를 구분할 때 세 번째 요소에 점은 1을 넣고 벡터는 0을 넣어서 구분한다. 이렇게 세 번째 요소까지 활용해 점과 벡터를 구분하면 앞서 언급한 아핀 공간에서의 점과 벡터의 모든 성질을 만족한다.
- 벡터 + 벡터 = 벡터 → 0 + 0 = 0
- 점 + 벡터 = 점 → 1 + 0 = 1
- 점 - 점 = 벡터 → 1 - 1 = 0
정리하자면 아핀 공간은 3차원 공간에서 z=1인 단면에 존재하는 무수한 벡터 공간의 원점을 의미한다. 이는 이동 변환을 선형 변환으로 구현해야 하기 때문에 발생한 개념이라고 볼 수 있다. 이를 통해 선형변환으로 이동을 표현할 수 있다.
유클리드 공간 (Euclidean Space)

Euclidean Space
유클리드 공간은 아핀 공간을 기반으로 하지만, 거리 또는 각도를 측정할 수 있는 내적 (inner product) 연산을 추가하여 크기 개념을 도입한 구조이다.
내적 (inner product): 두 벡터를 결합하여 스칼라 값을 계산하는 연산이다. 유클리드 공간에서는 내적을 이용하여 두 점 사이의 거리, 두 벡터 사이의 각도를 계산할 수 있다.
벡터 공간은 화살표의 연산만을 다루고, 아핀 공간은 점의 상대적인 위치 관계만을 다루는 반면, 유클리드 공간은 거리와 각도 같은 크기 개념까지 도입하여 3D 공간의 기하학적 성질을 완벽하게 표현할 수 있는 수학적 도구이다.
Homogeneous Coordinate

Homogeneous coordinate
동차좌표계 (Homogeneous Coordinate) :
차원사영 공간(Projective space)을
개의 좌표로 나타내는 좌표계로 2D 점 (x, y)의 동차 좌표는 (wx, wy, w) 형태로 표현된다. 여기서 w는 0이 아닌 임의의 실수이다. 즉, (2, 1, 1), (4, 2, 2), (6, 3, 3)은 모두 2D 좌표 (2, 1)을 동차 좌표로 표현한 것이다.
w 값에 따라 동차 좌표는 다른 공간을 나타낸다.
w = 1: 일반적인 2D Cartesian 공간
w ≠ 1: 투영 평면 (projection plane)
동차 좌표 (X, Y, w)가 주어졌을 때, 모든 것을 w로 나누면 (X/w, Y/w, 1) 을 얻는다. 이는 투영 평면 (w = 1) 위에 선분에 있는 점을 투영하는 것과 같다. 마지막으로 처음 두 성분 (X/w, Y/w)만 취하면 일반적인 2D Cartesian 좌표를 얻을 수 있다. 동차좌표로 조절하기 위해서는, 크기 변환과 회전 변환은 3차원 행렬로 변환해야한다.
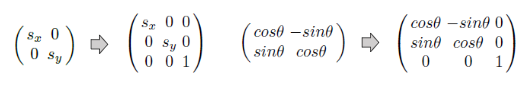
2D rotation to homogeneous coordinate
동차좌표계라는 개념은 여지껏 적용해왔던 원점에 고정되어있는 벡터만을 선형변환하는 벡터 공간이 아닌 벡터에 점을 추가한 아핀 공간을 다루기 때문에 주의가 필요하다. 예를 들어 아핀 공간에선 (x,y,z) = (1,2,3)의 좌표가 존재할 때, 이 좌표는 점일수도, 원점에서 (1,2,3)을 향하는 벡터일 수도 있다. 이렇게 표현하면 점인지 벡터인지 구분할 수 없어 이 둘을 구분하기 위해 사용하는 것이 동차좌표이다(예를 들어 2차원상의 점과 벡터를 2개가 아닌 3개의 요소로 표현한다.) 3차원 동차좌표를 4차원 좌표로 표시하면 3차원 실제 좌표는 (x/w,y/w,z/w)가 된다. (1,2,4,1) = (2,4,8,2) = (5, 10, 20, 5) 이며, 이 모든 동차좌표는 3차원 공간상의 한 점 (1,2,4)를 나타낸다. w = 0인 경우는 그 자체가 벡터(x,y,z)를 나타낸다.
2. Geometric Objects
Geometric ADTs
Geometric ADT는 점, 벡터와 같은 기하학 객체를 다루며, 이 객체들 간의 연산을 정의한다.
두 점의 차 (subtraction of two points)
점과 벡터의 합 (point-vector addition)
벡터와 벡터의 합 (vector-vector addition)
Line : 직선은 시작지점과 종료지점이 없는 끝없는 선이며, 선분은 시작지점과 종료지점이 있는 선이다. 이 선을 Point와 Vector 그리고 Scalar로 표현할 수 있다. 앞서 설명한 대로 점 p와 벡터 v의 합은 새로운 점 q를 생성한다. 이는 벡터 v만큼 점 p를 이동시킨 결과이다. 이 개념을 통해 선분을 다룰 수 있다. 선분의 시작점을 p라고 하고, 선분의 방향을 나타내는 방향 벡터를 v라고 하면, 선분상의 임의의 점 q는 다음과 같은 식으로 나타낼 수 있다.
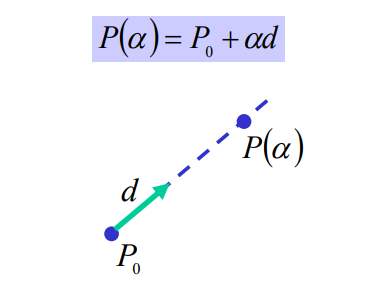
Lines
아핀 공간의 정의된 연산: 벡터 간의 덧셈, 벡터의 스칼라 곱셈 ,벡터와 점의 덧셈
아핀 공간의 정의되지 않은 연산: 두 점의 덧셈, 점의 스칼라 곱셈
하지만 정의되지 않는 두 연산의 요소를 갖는 아핀 합이라 불리는 연산이 있다.
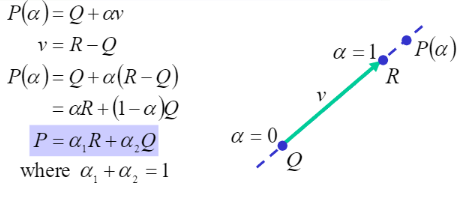
Affine Additions
벡터 v는 점과 점의 빼기로도 표현이 가능하다. v =R−Q를 선분방정식에 대입하면
P(α)=Q+α(R−Q)=αR+(1−α)Q가 된다. α를 α1, 1−α를 α2라고 두면, P=α1 R+α2 Q(단,α1+α2=1)이 된다. 두 알파의 합이 1이면, 딱 점 Q와 점 R을 잇는 그 사이의 공간이 정의된다. 바로 시작, 종료지점이 있는 선분이 생기는 것이다.
Covexity : 볼록한 Convex 객체는 객체 내에 임의의 두 점을 연결하는 선분 위에 놓인 임의의 점이 객체 내에 있는 객체이다. 볼록 도형은 도형 안의 두점을 연결하는 선분 위의 모든 점이 역시 그 도형 안에 존재하는 성질을 가진 도형이다.
Convex hull : 컨벡스 헐(Convex Hull)은 한 집합의 점들을 가장 잘 감싸는 볼록 다각형을 의미합니다. 쉽게 말해, 여러 점들을 둘러싸는 가장 최소한의 울타리이다. n개의 점 P = {p1, p2, ..., pn} 에 대한 컨벡스 헐(Convex Hull) H 는 다음 두 조건을 만족하는 최소 면적의 다각형이다.
- 모든 점 포함: H 내부 또는 H의 경계에 모든 p가 포함된다.
- 볼록성: H의 임의 두 점 a 와 b 를 연결하는 선분 ab 의 모든 점 또한 H 내부 또는 H의 경계에 포함된다.
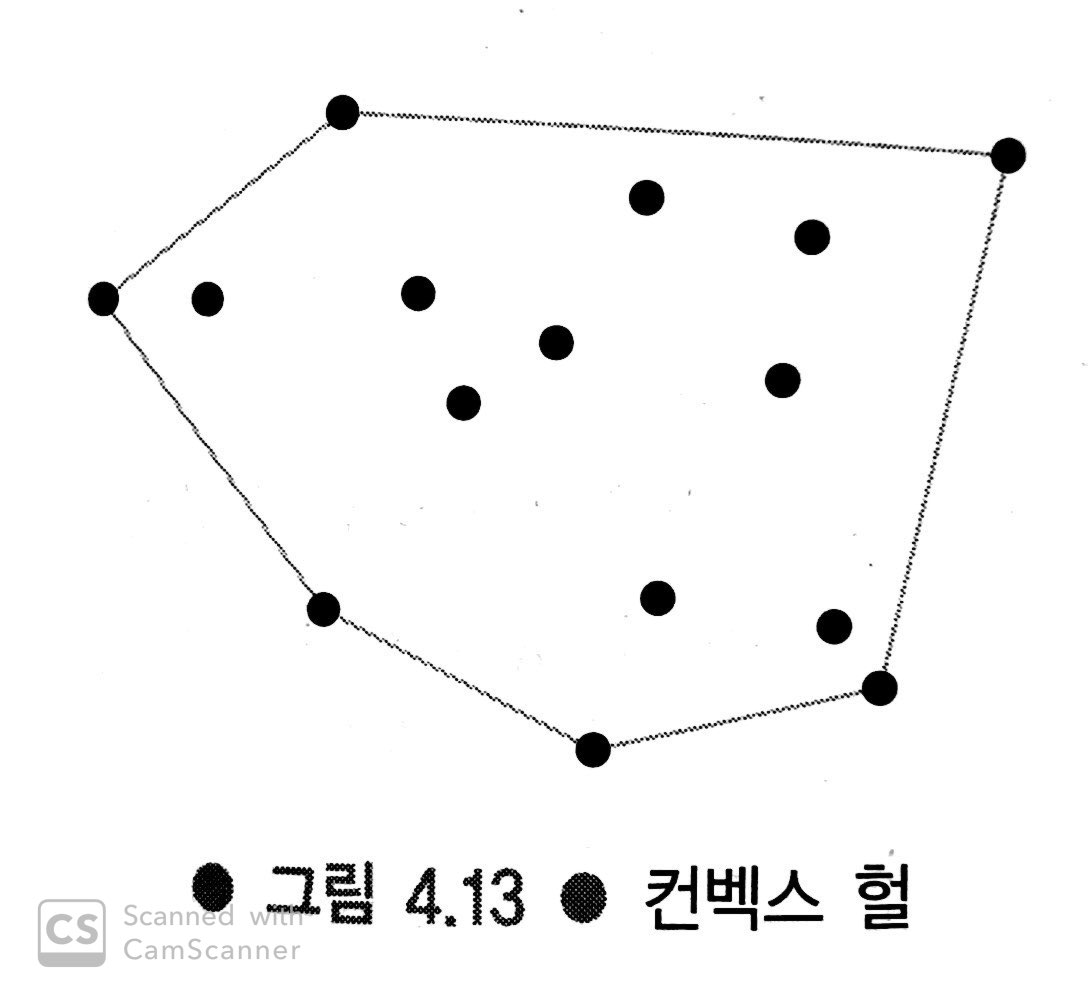
Convex hull
볼록 도형과 아핀 합 : 볼록 도형을 판별하는 데는 아핀합 (affine sum) 개념이 유용하다. 아핀 합: 점 p1과 p2에 대해 스칼라 α (0 ≤ α ≤ 1)와 β (α + β = 1)를 사용하여 다음과 같이 계산되는 점 q이다. q = αp1 + βp2 . 볼록 도형 S에서 임의의 두 점 p1과 p2를 선택했을 때, 이 두 점의 아핀 조합 q (0 ≤ α ≤ 1)가 항상 S 안에 존재한다면 S는 볼록 도형이라고 할 수 있다.
Plane
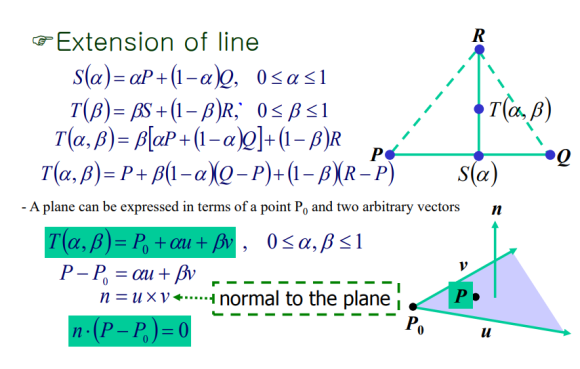
면은 선을 움직인 흔적으로 생긴 공간을 의미하고 선은 점을 움직인 흔적으로 생긴 공간이다. 선은 점에 벡터를 더한 방정식으로 표현하였으므로, 면 또한 점과 벡터를 잘 건드려서 방정식으로 표현할 수 있다.
Normal to the plane
면의 방향은 Cross Products와 같은 말이다. 색종이를 책상 위에 올렸다고 하자. 이 색종이의 방향은 수직인 방향인 위쪽을 의미하는 것이다.
Geometry and Topology
Geomety: 객체의 실제적인 모양과 vertex의 위치에 대한 정보를 말한다.
Topology: 객체의 연결 관계에 대한 정보를 말한다. 점들 간의 연결, 선분 (edge)의 연결, 면 (face)들의 연결 등 객체를 구성하는 요소들이 어떻게 서로 연결되어 있는지를 나타낸다.
'Mathematics > Linear Algebra' 카테고리의 다른 글
| Linear Algebra [2] : 함수 최적화 (Function Optimization) (1) | 2024.10.29 |
|---|---|
| Linear Algebra [1] : 행렬 분해 (Matrix Factorization) (0) | 2024.10.11 |