
Forward kinematics는 로봇공학 및 기계공학에서 로봇 매니퓰레이터의 관절 변수를 기반으로 해당 말단 이펙터(end effector)의 위치와 자세를 계산하는 과정이다. 이는 로봇의 각 관절에 대해 주어진 회전각 또는 변위와 같은 값을 이용하여 공간상에서의 이펙터의 위치를 수학적으로 결정하는 것을 말한다. 일반적으로 로봇의 구조적 체인과 관절 정보는 변환 행렬(transformation matrix)이나 좌표계를 사용해 표현되며, 이를 통해 기구학적 연산을 수행한다. Forward kinematics는 로봇의 작업 공간(workspace)을 분석하거나 목표 지점에 도달할 수 있는지를 평가하는 데 중요한 역할을 하며, 이를 계산하기 위해 Denavit-Hartenberg(DH) 매개변수와 같은 방법론이 자주 활용된다.
조인트 공간과 카르테시안 공간 (Joint Space and Cartesian Space )

로봇 팔의 기구학에서 조인트 공간(Joint Space)과 카르테시안 공간(Cartesian Space)은 로봇 팔의 움직임을 표현하는 두 가지 기본적인 방식이다. 조인트 공간은 로봇의 각 관절 상태를 각도로 나타낸다. 예를 들어, 두 개의 관절로 이루어진 로봇 팔에서는 첫 번째 관절의 각도 θ1과 두 번째 관절의 각도 θ2로 조인트 공간에서의 상태를 표현할 수 있다. 이 값들은 로봇 팔이 어떤 각도로 움직였는지를 나타내는 데 유용하며, 로봇의 동작 계획을 수학적으로 단순화할 수 있다. 반면, 카르테시안 공간은 로봇 팔의 끝부분(엔드 이펙터)의 위치를 실제 작업 환경의 좌표계로 나타낸다. 예를 들어 로봇 팔이 작업 테이블에서 특정한 지점에 물건을 집어야 할 때, 엔드 이펙터의 좌표를 (px,py)와 같이 2D 좌표로 표현한다. 카르테시안 공간은 로봇의 작업 결과를 직관적으로 보여주며, 물리적인 위치를 기반으로 로봇의 동작을 설계하거나 조정하는 데 유용하다.
조인트 공간에서 카르테시안 공간으로 변환하는 공식은 로봇 팔의 기하학적 구조와 삼각함수를 기반으로 한다. 이 변환 과정은 주어진 각 관절의 각도와 길이를 이용해 로봇의 끝부분(엔드 이펙터)의 좌표를 계산하는 것이다. 로봇 팔이 2개의 관절로 구성된 2D 평면에서 움직이는 경우, 엔드 이펙터의 -좌표와 -좌표는 다음과 같이 계산된다
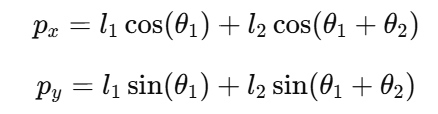
회전 (Rotation)
로봇의 움직임과 강체 운동을 수학적으로 표현하기 위해 좌표계, 회전행렬, 그리고 동차 변환행렬을 활용한다. 강체의 움직임은 **고정 좌표계({s}\{s\})**와 **물체 좌표계({b}\{b\})**를 사용해 표현된다. 고정 좌표계는 움직이지 않는 기준 좌표계이며, 물체 좌표계는 강체에 부착된 좌표계로 강체의 움직임과 방향을 설명한다. 강체의 위치는 고정 좌표계에서 물체 좌표계의 원점을 나타내는 벡터 p\mathbf{p}로 나타내고, 방향은 **회전행렬(RR)**로 표현된다. RR은 물체 좌표계의 단위축을 고정 좌표계에서 표현한 행렬로, 물체의 자세를 설명한다.
회전행렬 RR은 강체의 방향을 나타내며 몇 가지 중요한 성질을 가진다. 첫째, 회전행렬은 직교행렬로 RTR=IR^T R = I를 만족하며, 이는 행렬의 열벡터가 모두 단위벡터이고 서로 직교한다는 것을 의미한다. 둘째, 회전행렬의 행렬식은 1로, 이는 크기나 모양의 왜곡 없이 순수한 회전을 수행함을 보장한다. 셋째, 두 회전행렬의 곱 또한 회전행렬이며, 회전행렬의 역행렬은 그 전치행렬과 같다. 이러한 성질로 인해 회전행렬은 3차원 공간의 방향을 나타내는 데 매우 유용하며, 이를 특수직교군(Special Orthogonal Group) SO(3)SO(3)라고 부른다.
회전행렬은 강체의 방향을 표현하거나, 기준 좌표계를 변환하거나, 벡터를 특정 축을 기준으로 회전시키는 데 활용된다. 예를 들어, 좌표계 {b}\{b\}에서 좌표계 {c}\{c\}의 방향을 회전행렬 RbcR_{bc}로 나타낼 수 있다. 기준 좌표계를 변환할 때는 RabR_{ab}와 같은 회전행렬을 이용해 벡터를 {a}\{a\}에서 {b}\{b\}로 변환한다. 또한, 회전축 w^\mathbf{\hat{w}}와 각도 θ\theta를 중심으로 회전시키는 회전행렬은 반대칭 행렬([w^][\mathbf{\hat{w}}])을 사용하여 계산된다. 이러한 방식으로 회전행렬은 로봇 공학, 그래픽스, 물리 시뮬레이션 등에서 활용된다.
강체의 위치와 방향을 동시에 표현하려면 동차 변환행렬(Homogeneous Transformation Matrix) TT을 사용한다. TT은 강체의 위치를 나타내는 벡터 p\mathbf{p}와 방향을 나타내는 회전행렬 RR을 하나의 행렬로 묶은 형태다. 예를 들어, 변환행렬 TT는 다음과 같이 나타낼 수 있다:
T=[Rp01]T = \begin{bmatrix} R & \mathbf{p} \\ 0 & 1 \end{bmatrix}
이 동차 변환행렬은 강체의 자세(위치와 방향)를 설명하며, 벡터나 좌표계를 회전시키고 이동시키는 데 사용된다. 변환행렬은 회전행렬과 마찬가지로 직교성과 결합법칙을 만족하며, 변환행렬의 곱과 역행렬도 변환행렬의 성질을 유지한다.
강체 운동은 **트위스트(Twist)**와 **렌치(Wrench)**를 통해 더욱 직관적으로 표현된다. 트위스트는 강체의 각속도와 선속도를 하나의 6차원 벡터로 표현하며, 강체의 회전과 병진 운동을 동시에 설명한다. 트위스트는 고정 좌표계에서의 공간 트위스트(Vs\mathbf{V}_s)와 물체 좌표계에서의 물체 트위스트(Vb\mathbf{V}_b)로 나뉜다. 반면 렌치는 강체에 가해지는 힘과 모멘트를 하나로 묶어 표현하며, 강체의 움직임에 대한 외부 영향을 설명하는 데 사용된다. 렌치와 트위스트는 각각 변환행렬을 이용해 서로 다른 기준 좌표계에서 변환이 가능하다.
트위스트는 강체의 회전축과 병진 운동을 결합한 스크류 축(Screw Axis)으로 해석될 수 있다. 스크류 운동은 축을 따라 이동하며 동시에 회전하는 운동을 의미하며, 이를 통해 강체의 복잡한 움직임을 간단히 모델링할 수 있다. 강체의 모든 이동은 스크류 축을 기준으로 회전과 병진 운동의 조합으로 설명될 수 있다. 이러한 스크류 운동의 지수 좌표 표현은 로봇 공학에서 로봇 팔의 동작을 설계하거나 제어하는 데 중요한 도구가 된다.
결론적으로, 강체의 움직임을 수학적으로 표현하기 위해 회전행렬, 동차 변환행렬, 트위스트, 렌치를 사용한다. 이 도구들은 로봇 공학과 물리학에서 위치와 방향을 분석하고 제어하는 데 필수적이며, 로봇 팔의 경로 계획, 작업공간 분석, 동작 제어 등 다양한 응용 분야에서 활용된다. 이러한 수학적 표현을 이해하고 적용하는 것은 로봇의 복잡한 움직임을 정확히 설명하고 제어하는 데 핵심적인 역할을 한다.
Forward Kinematics

로봇공학에서 정기구학은 로봇의 관절 값(각도나 거리)을 이용해 엔드 이펙터(End-Effector)의 위치와 방향을 계산하는 과정이다. 로봇의 주요 작업은 엔드 이펙터를 원하는 위치로 정확히 이동시키는 것이며, 이를 위해 관절의 움직임과 엔드 이펙터의 움직임 간의 관계를 이해하는 것이 필수적이다. 정기구학은 로봇 설계와 제어의 기본 원리를 제공하며, 이를 통해 로봇이 작업 공간에서 어떻게 움직이는지 계산할 수 있다.
정기구학의 기본 원리
정기구학은 로봇 관절의 값을 통해 엔드 이펙터의 위치와 방향을 계산하는 것을 목표로 한다. 이는 수학적으로 로봇의 기구학적 구조를 기반으로 삼각함수, 회전행렬, 변환행렬 등을 이용해 이루어진다. 예를 들어, 2D 평면에서 두 개의 회전 관절을 가진 로봇의 경우, 관절 각도와 링크의 길이를 알고 있다면 삼각함수를 사용해 엔드 이펙터의 위치를 계산할 수 있다.
정기구학의 두 가지 방법
- PoE(Product of Exponentials) 공식
PoE 공식은 각 관절이 로봇의 링크에 스크류 운동을 가한다고 가정하여, 고정 좌표계와 엔드 이펙터 좌표계 간의 변환을 통해 엔드 이펙터의 위치와 방향을 계산한다. 이 방법은 3D 로봇에도 쉽게 확장 가능하며, 스크류 축과 행렬 지수를 사용해 강체의 복잡한 움직임을 체계적으로 표현한다. - D-H(Denavit-Hartenberg) 파라미터
D-H 파라미터는 각 관절과 링크의 위치 및 방향을 체계적으로 표현하는 방법이다. 이 방법은 정기구학의 계산을 단순화하기 위해 각 링크의 상대적인 위치를 수학적으로 나타내는 방식이다. 이 파라미터는 주로 3D 로봇의 정기구학 계산에 사용된다.
쉬운 예시: 2D 평면의 로봇 팔
2D 평면에서 두 개의 회전 관절(2R 로봇)을 가진 로봇을 예로 들어 보자. 첫 번째 관절의 각도가 θ1=30∘\theta_1 = 30^\circ, 두 번째 관절의 각도가 θ2=45∘\theta_2 = 45^\circ이며, 두 링크의 길이가 각각 l1=3l_1 = 3, l2=2l_2 = 2라고 가정하자.
- 첫 번째 링크의 끝 위치 계산:
첫 번째 링크의 끝 위치는 첫 번째 관절의 각도를 기준으로 계산된다. 이를 삼각함수를 이용해 계산하면:

3D 로봇 팔에서의 정기구학
3D 공간에서 정기구학은 2D와 달리 더 복잡하다. 각 관절의 회전과 링크의 상대적 위치를 3D 변환행렬로 표현해야 한다. 이를 위해 PoE 공식이나 D-H 파라미터를 사용한다. PoE 공식에서는 각 관절이 고정 좌표계에서 스크류 축을 기준으로 움직인다고 가정하며, 변환행렬의 곱으로 엔드 이펙터의 위치와 방향을 계산한다.
예를 들어, 회전 관절이 3개 있는 3D 로봇(3R 로봇)을 생각해 보자. 각 관절의 회전값 θ1,θ2,θ3\theta_1, \theta_2, \theta_3과 각 관절의 스크류 축 S1,S2,S3S_1, S_2, S_3가 주어졌을 때, 엔드 이펙터의 위치는 다음과 같이 계산된다.

여기서 MM은 모든 관절이 초기 위치(0도)에 있을 때 엔드 이펙터의 자세(위치와 방향)를 나타내는 행렬이다.
기구학적 속성 (Kinematic Properties)
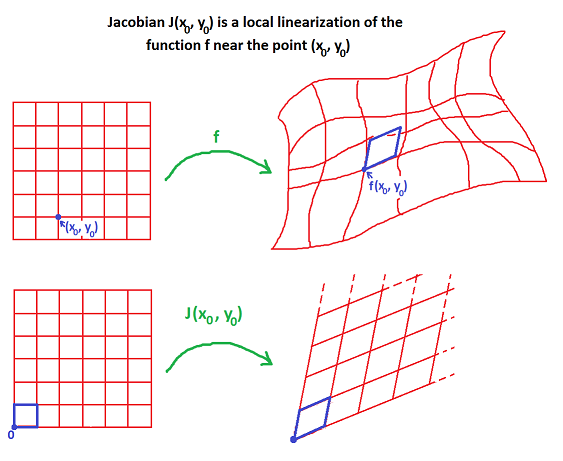
*기구학적 속성(Kinematic Properties)**은 로봇의 운동을 설명하는 중요한 특성으로, 주로 속도와 가속도를 기반으로 엔드 이펙터와 관절의 관계를 수학적으로 표현한다. 이 속성은 로봇이 작업 공간에서 효율적이고 정확하게 움직일 수 있도록 제어하는 데 필수적이다. 특히, 기구학적 속성은 야코비안(Jacobian)을 중심으로 정의되며, 로봇의 운동학적 분석에서 핵심적인 역할을 한다.
1. 야코비안(Jacobian)의 정의
로봇의 엔드 이펙터 속도와 관절 속도 간의 관계를 나타내는 도구가 야코비안 행렬이다. 엔드 이펙터의 위치와 방향은 관절 값의 함수로 표현되는데, 이 관계를 시간에 따라 미분하면 관절의 변화율과 엔드 이펙터의 속도 간의 선형 관계를 얻을 수 있다:
v=J(Θ)Θ˙\mathbf{v} = J(\Theta) \dot{\Theta}
여기서:
- v\mathbf{v}: 엔드 이펙터의 선속도와 각속도를 포함하는 6차원 속도 벡터.
- J(Θ)J(\Theta): 야코비안 행렬로, 관절 속도를 엔드 이펙터 속도로 변환하는 역할을 한다.
- Θ˙\dot{\Theta}: 관절 속도의 벡터.
야코비안은 엔드 이펙터의 움직임을 정량적으로 이해하는 데 중요한 역할을 하며, 로봇의 작업 공간에서 움직임의 제어를 가능하게 한다.
2. 야코비안의 구성
야코비안 행렬 J(Θ)J(\Theta)는 선속도 부분과 각속도 부분으로 나뉜다. 각각의 구성은 다음과 같다:
- 선속도 (Linear Velocity):
- 로봇의 엔드 이펙터가 작업 공간에서 얼마나 빠르게 이동하는지를 나타낸다.
- 각속도 (Angular Velocity):
- 엔드 이펙터가 작업 공간에서 얼마나 빠르게 회전하는지를 나타낸다.
J(Θ)J(\Theta)는 일반적으로 6×n6 \times n 크기의 행렬로, 여기서 nn은 로봇 관절의 개수이다. 이 행렬은 각 관절의 움직임이 엔드 이펙터의 위치와 방향에 어떻게 영향을 미치는지 설명한다.
3. 야코비안의 활용
3.1 속도 계산
야코비안을 사용하면 주어진 관절 속도를 기반으로 엔드 이펙터의 선속도와 각속도를 계산할 수 있다. 이는 로봇이 작업 공간에서 특정 방향으로 움직이거나 회전해야 할 때 유용하다.
3.2 역기구학 문제
야코비안은 정기구학뿐만 아니라 역기구학에서도 사용된다. 엔드 이펙터의 목표 속도가 주어졌을 때, 이를 실현하기 위한 관절 속도를 계산하는 데 사용된다:
Θ˙=J−1v\dot{\Theta} = J^{-1} \mathbf{v}
여기서 J−1J^{-1}은 야코비안의 역행렬이다. 야코비안이 정방행렬이 아니거나 비특이성을 가지는 경우, 의사역행렬을 사용하여 해결한다.
3.3 특이점 분석
야코비안을 통해 로봇의 **특이점(Singularity)**을 분석할 수 있다. 특이점은 야코비안 행렬이 역행렬을 가지지 못하는 지점으로, 이 경우 엔드 이펙터가 특정 방향으로 움직이지 못하거나 무한대의 관절 속도를 요구하게 된다. 이는 로봇 설계와 제어에서 중요한 문제로, 로봇이 특이점에 도달하지 않도록 운동을 계획해야 한다.
4. 야코비안의 형식
야코비안은 두 가지 방식으로 정의될 수 있다:
- 스페이스 야코비안 (Space Jacobian):
- 고정 좌표계 기준으로 정의되며, 엔드 이펙터의 속도를 고정 좌표계에서 표현한다.
- 바디 야코비안 (Body Jacobian):
- 물체 좌표계 기준으로 정의되며, 엔드 이펙터의 속도를 물체 좌표계에서 표현한다.
스페이스 야코비안은 고정 좌표계를 기준으로 계산하므로 로봇의 관절 순서대로 영향을 계산하는 반면, 바디 야코비안은 엔드 이펙터에서부터 역순으로 계산한다. 두 방식은 변환 관계를 통해 서로 변환이 가능하다.
5. 예시: 2R 로봇의 야코비안

6. 결론
기구학적 속성, 특히 야코비안은 로봇 공학에서 엔드 이펙터의 움직임을 이해하고 제어하는 데 필수적이다. 이를 통해 로봇이 작업 공간에서 어떻게 움직이는지, 목표 위치나 방향에 도달하려면 관절이 어떻게 조정되어야 하는지를 분석할 수 있다. 야코비안은 또한 특이점 분석, 속도 및 힘 전달 계산, 역기구학 문제 해결 등 다양한 로봇 응용 분야에서 핵심적인 도구로 사용된다. 이러한 기구학적 속성을 이해하는 것은 로봇 설계와 제어의 기본을 형성하며, 복잡한 로봇 시스템을 구현하는 데 매우 중요하다.
'Computer Graphics > Animation' 카테고리의 다른 글
| Animation Kinematics [3] : 운동학 수치 해석 (Kinematics Numerical approach) (0) | 2024.12.14 |
|---|---|
| Animation Kinematics [2] : 역기구학 (Inverse Kinematics) (1) | 2024.10.08 |
| Animation Kinematics [0] : 운동학 기초 (Fundamentals to Kinematics) (0) | 2024.09.19 |