
1. 딥러닝 모델
딥러닝(Deep Learning, DL)은 머신 러닝(Machine Learning, ML)의 한 분야로, 머신 러닝은 인공지능(AI)의 하위 개념이다. AI는 사람의 지능이나 행동을 모방하는 기술을 의미하며, 머신 러닝은 데이터를 통해 컴퓨터가 스스로 학습하도록 하는 기술이다. 딥러닝은 인간의 뇌, 특히 뉴런의 구조를 모방한 신경망을 이용해 복잡한 학습을 수행하는 기법이다. 현재에는 사람의 고유한 능력으로 컴퓨터가 절대 할 수 없었던 것처럼 여겨졌던 상상을 하고 그것을 그려내는 모델 등이 나오면서 주목을 받고 있다.

불확실성을 직관적으로 이해하자면, 예측하기 어려운 상황을 떠올리면 좋다. 예를 들어 주사위를 던질 때 결과가 어떤 숫자가 나올지 알 수 없어서 불확실성이 큰 상태인데, 여기서 가능한 결과가 여섯 가지이므로 예측이 쉽지 않다. 반면, 만약 주사위가 고장 나서 항상 '6'만 나오는 상황이라면, 결과는 항상 똑같아 불확실성이 전혀 없게 된다. 따라서 불확실성이 크다는 것은 결과가 다양한 가능성을 가지므로 예측하기 어렵고, 얻을 수 있는 정보도 많다는 뜻이다.
엔트로피 H(X)H(X)는 정보이론에서 불확실성의 척도로, 확률 변수 XX의 모든 가능한 값에 대한 확률을 기반으로 계산된다. 엔트로피의 수식은 다음과 같다

- 불확실성의 양 계산: 어떤 사건의 불확실성은 발생 확률 P(xi)가 낮을수록 커진다. 이를 나타내기 위해 log2P(xi)를 사용하며, 이는 확률이 낮을수록 높은 음수 값을 제공한다. −log2P(xi)는 이를 양수로 바꿔, 확률이 낮은 사건에 더 많은 정보량을 할당한다.
- 모든 가능한 결과의 평균 정보량: 실제로 발생할 수 있는 모든 사건에 대한 불확실성을 측정하기 위해 각 사건의 정보량에 해당 사건이 발생할 확률 P(xi)을 곱한다. 이렇게 함으로써 발생 가능성이 높은 사건은 정보량이 적고, 드문 사건일수록 정보량이 많아지게 된다.
- 모든 정보량의 합: 마지막으로, 모든 가능한 사건의 평균 정보량을 구하기 위해 합을 구해 엔트로피를 얻는다.
예를 들어, 주사위를 던질 때 엔트로피를 계산해 보자. 주사위의 각 면이 나올 확률은 동일하게 P(xi)=16P(x_i) = \frac{1}{6}이다. 이 경우 엔트로피 H(X)H(X)는 다음과 같이 계산된다.

여기서 각 면이 나올 확률이 동일하므로 불확실성이 최대인 상황이다. 엔트로피 값 2.582.58은 이 사건의 불확실성을 나타내며, 이는 주사위를 던질 때 결과를 예측하기가 어렵다는 것을 의미한다. 반면, 만약 동전을 던져서 앞면이 나올 확률이 100%라면 H(X)H(X)는 0이 되어, 예측할 수 있는 정보가 전혀 없음을 보여준다. 이처럼 엔트로피는 사건의 확률 분포에 따라 불확실성을 수치적으로 표현해 주는 중요한 개념이다.
주사위와 동전의 엔트로피는 다음과 같다


위의 수식을 간결하게 바꾸어 보면, 각 사건 p(xi)가 동일한 확률을 가지는 경우에 엔트로피는 다음과 같이 표현될 수 있다.

여기서 x 값이 작아질수록 −logx값은 기하급수적으로 커지며, 이는 확률 가 작아질 때 불확실성이 증가함을 의미한다. 즉, x가 작아지는 것보다 logx가 커지는 폭이 훨씬 크기 때문에, 전체 엔트로피는 증가하게 된다. 이러한 특성은 사건의 확률이 낮아질수록 발생 가능성이 적어지므로 불확실성이 높아지는 것을 직관적으로 설명해준다.
1.2 예시 : 공 꺼내기
전체 공이 100개인 상황을 두 가지 예시로 살펴보면, 첫 번째 경우에는 빨간색 공이 하나뿐이고 나머지 99개가 검은색인 경우를 생각할 수 있다. 이때 검은색 공이 나올 확률은 P(검은색)=99/100, 빨간색 공이 나올 확률은 P(빨간색)=1/100이다. 반면, 두 번째 경우에는 50개의 빨간색 공과 50개의 검은색 공이 있다. 이 경우에는 두 색상의 공이 나올 확률이 동일하므로 P(검은색)=50/100이다. 직관적으로 보면 첫 번째 사례는 검은색 공이 나올 확률이 높아 불확실성이 적을 것 같지만, 실제로 엔트로피를 계산해보면 후자, 즉 두 번째 사례의 엔트로피가 훨씬 더 크다는 것을 알 수 있다. 이는 사건의 불확실성이 빨간색과 검은색 공의 비율이 균등할 때 더 높아지기 때문으로, 다양한 결과가 가능할수록 엔트로피가 증가하는 것을 보여준다.
Cross-Entropy
원래의 교차 엔트로피(cross entropy)는 예측 모델이 실제 분포 q를 알지 못할 때, 이 분포를 모델링하여 예측하고자 할 때 사용된다. 예를 들어, 예측 모델링을 통해 얻은 확률 분포를 p(x)라고 할 때, 교차 엔트로피는 실제 분포 q와 모델이 예측한 분포 p 간의 차이를 측정하는 방법으로 정의된다. 수식적으로는 다음과 같이 표현된다:

이 수식은 실제 분포 에 따라 가중치를 부여받은 예측 분포 p의 로그값을 합산하여, 두 분포 간의 차이를 수치적으로 나타낸다. 교차 엔트로피는 모델이 실제 데이터를 얼마나 잘 예측하고 있는지를 평가하는 데 중요한 역할을 하며, 최적의 예측 모델을 개발하는 과정에서 손실 함수로 자주 사용된다.
크로스 엔트로피는 두 확률 분포 간의 차이를 구하는 데 사용되며, 딥러닝에서는 실제 데이터의 확률 분포 q와 학습된 모델이 계산한 확률 분포 간의 차이를 평가하는 데 활용된다. 예를 들어, 가방에 빨간색, 녹색, 노란색 공이 각각 0.8, 0.1, 0.1의 비율로 들어 있다고 가정하자. 하지만 모델의 직감적으로 예측한 비율은 0.2, 0.2, 0.6이라면, 이때 실제 분포 q를 알고 있는 훈련 데이터를 사용하여 크로스 엔트로피를 계산할 수 있다. 엔트로피와 크로스 엔트로피는 다음과 같이 계산된다. 엔트로피는 실제 분포에서의 불확실성을 측정하고, 크로스 엔트로피는 모델이 예측한 확률 분포와 실제 분포 간의 차이를 나타낸다. 이러한 계산을 통해 실제 값과 예측값의 차이(dissimilarity)를 측정하고, 이를 기반으로 모델의 성능을 개선하는 데 활용할 수 있다.

Kullback-Leibler Divergence
"KL Divergence" 또는 Kullback-Leibler Divergence는 서로 다른 두 확률 분포 간의 차이(dissimilarity)를 측정하는 데 사용되는 지표이다. 이 개념은 엔트로피와 크로스 엔트로피의 개념을 활용하여 두 엔트로피 간의 차이로 정의된다. KL Divergence의 정의는 다음과 같다: 두 분포 qq (실제 분포)와 pp (예측 분포)가 있을 때, KL Divergence는

로 표현된다. 여기서 pp는 모델이 예측한 확률 분포, qq는 실제 분포이며, 이 식은 pp 분포에 따라 가중치가 부여된 qq 분포의 로그 비율을 합산하는 방식으로 계산된다. 연속 확률 분포의 경우, 합(sum) 대신 적분(integral)을 사용하여 계산된다. KL Divergence는 주어진 예측 분포가 실제 분포에 얼마나 차이가 나는지를 수치적으로 나타내며, 이를 통해 모델의 성능을 평가하고 개선하는 데 중요한 역할을 한다.

cross-entropy = H_p(q)는 실제 entropy = H(q) 보다 항상 크기 때문에 KL Divergence 는 항상 0보다 큰 값을 갖게된다. 예측 분포인p 를 실제분포 q에 가깝게 하는 것이, 예측모형이 하고자하는 것이며, p가 q에 가까이갈 수록 KL Divergence 0에 가까워질 것이다. 그리고 H(q) 는 고정이기 때문에, H_p(q)를 최소화 시키는 것이 예측 모형을 최적화 시키는 것이라고 할 수 있다. 따라서 cross-entropy 를 최소화 시키는 것이 KL Divergenece 를 최소화 시키는 것이며, 이것이 불확실성을 제어하고자하는 예측모형의 실질적인 목적이라고 볼 수 있다. 교차 엔트로피는 Hp(q)H_p(q)로 정의되며, 항상 실제 엔트로피 H(q)보다 크기 때문에 KL Divergence는 항상 0보다 큰 값을 갖는다. 예측 분포 p를 실제 분포 에 가깝게 만드는 것이 예측 모델의 주요 목표이며, 가 q에 가까워질수록 KL Divergence는 0에 가까워진다. 여기서 H(q)는 고정된 값이기 때문에, 교차 엔트로피 H_p(q)를 최소화하는 것이 예측 모델을 최적화하는 방법으로 간주될 수 있다. 따라서 교차 엔트로피를 최소화하는 것은 KL Divergence를 최소화하는 것이며, 이는 불확실성을 제어하려는 예측 모델의 실질적인 목적이라고 할 수 있다. 이러한 과정은 모델이 실제 데이터를 더 잘 예측하도록 돕고, 궁극적으로 성능을 향상시키는 데 기여한다.
KL-Divergence는 텐서플로우 공식 문서에 다음과 같이 구현되어 있습니다.
loss = y_true * log(y_true / y_pred)

KL-Divergence(측도)는 두 확률 분포 와 Q가 얼마나 다른지를 측정하는 방법으로, 통계적으로 는 사후 분포를, 는 사전 분포를 의미한다. TensorFlow 공식 문서에서 정의된 바에 따르면, KL-Divergence는 실제 값 ytrue(P)가 가지는 분포와 예측 값 ypred(Q)가 가지는 분포 간의 차이를 확인하는 방법이다. 이 값이 낮을수록 두 분포는 유사하다고 해석할 수 있으며, 이는 정보 이론에서 엔트로피(Entropy)가 값이 낮을수록 랜덤성이 낮다는 해석과 유사하다. 이러한 유사한 해석이 가능한 이유는 KL-Divergence에 크로스 엔트로피(Cross-Entropy) 개념이 이미 포함되어 있기 때문이다. 이를 통해 KL-Divergence는 모델의 예측 분포가 실제 분포에 얼마나 잘 맞추어져 있는지를 평가하는 중요한 도구로 사용된다.
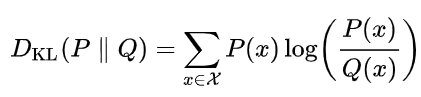
KLD와 크로스 엔트로피
Kullback-Leibler Divergence(KLD)와 크로스 엔트로피는 정보 이론에서 중요한 개념으로, 로그를 사용하여 정보량을 효과적으로 표현한다. 정보량은 사건의 발생 확률에 따라 달라지며, 확률이 높을수록 그 사건은 매우 당연하게 일어나는 것으로 인식되지만, 확률이 낮으면 그 사건은 자주 일어나지 않는 특별한 사건으로 간주된다. 또한, 엔트로피는 평균 정보량을 나타내는 지표로, 확률 분포의 불확실성을 측정한다. 이를 통해 KLD와 크로스 엔트로피는 서로 다른 확률 분포 간의 차이를 측정하고, 예측 모델의 성능을 평가하는 데 활용된다. 이들 개념은 데이터의 랜덤성 및 정보의 특성을 이해하는 데 필수적이다.
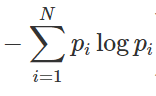
엔트로피는 예측할 수 있는 여러 상황이 각각 발생할 확률을 바탕으로 불확실성을 측정하는 지표이다. 예를 들어, 5개 상황이 각각 0.2의 확률로 발생한다고 가정할 때, 엔트로피는 H(P)=−∑i=15p(xi)logp(xi)=−5×0.2log(0.2)H(P) = -\sum_{i=1}^{5} p(x_i) \log p(x_i) = -5 \times 0.2 \log(0.2)로 계산된다. 이제 KL-Divergence(KLD)에 왜 크로스 엔트로피가 포함되는지를 살펴보면, 여기서 pp는 실제 세계에서 관찰하여 얻은 확률 분포(실제 확률 분포 PP)를 의미하고, qq는 모델이 예측한 확률(확률 분포 PP로 근사될 분포 QQ)을 나타낸다. KLD는 크로스 엔트로피를 사용하여 두 분포 간의 차이를 측정하므로, 모델이 실제 데이터를 얼마나 잘 예측하고 있는지를 평가하는 데 중요한 역할을 한다. 이러한 관계를 통해 KLD와 크로스 엔트로피는 상호 연관되어 있으며, 모델 성능을 개선하기 위한 지표로 활용된다.
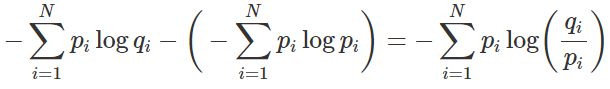
KL-Divergence는 다음과 같이 표현될 수 있다: KLD=Cross-Entropy−Entropy\text{KLD} = \text{Cross-Entropy} - \text{Entropy}. 이 식을 다시 나누어 보면 왼쪽 항은 한 듯이 Entropy에서 Entropy를 빼는 것처럼 보일 수 있지만, 사실상 맨 앞의 식에서 로그 안의 값은 모델이 예측한 확률 qq를 나타내므로, 이는 실제로 크로스 엔트로피에서 엔트로피를 빼는 형태가 된다. 즉, 크로스 엔트로피는 모델의 예측 분포가 실제 분포와 얼마나 다른지를 측정하며, 엔트로피는 실제 분포의 불확실성을 나타내기 때문에, 이 둘의 차이를 통해 KL-Divergence는 모델의 예측 성능을 정량적으로 평가하는 지표로 활용된다. 이는 모델이 실제 데이터를 얼마나 잘 설명하는지를 나타내는 중요한 관계를 형성한다.
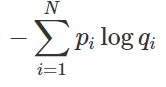
Cross-Etnropy
결과적으로 모델이 예측한 확률분포(Q)의 정보량과 실제 확률분포(P) 정보량의 차이를 계속 학습함으로써 Q를 P에 근사한다고 표현할 수 있습니다. 그래서 이에 대한 차이(정보량)를 분포가 유사한지에 대한 정도로 다시 해석할 수 있는 것입니다. 결과적으로, 크로스 엔트로피는 모델이 예측한 확률 분포 QQ의 정보량과 실제 확률 분포 PP의 정보량 간의 차이를 측정함으로써, 모델이 QQ를 PP에 점차 근사하도록 학습하는 과정을 나타낸다. 이 과정에서 모델은 두 분포 간의 차이를 최소화하려고 하며, 이를 통해 분포가 유사한 정도를 정량적으로 해석할 수 있다. 즉, 크로스 엔트로피를 최소화하는 것은 모델이 실제 데이터를 얼마나 잘 설명하는지를 평가하고, 예측 성능을 개선하는 데 중요한 역할을 한다. 이러한 차이를 학습함으로써 모델은 점점 더 정확한 예측을 수행할 수 있게 된다.
모델 학습에서의 KLD
우리가 일반적으로 분류(Classification) 문제에서 이진 또는 범주형 크로스 엔트로피를 사용하는 것은 KL-Divergence(KLD)를 사용하는 것과 사실상 동일하다고 볼 수 있다. 여기서 엔트로피에 해당하는 부분은 실제 값으로 고정되어 있으므로(손실 최소화에 영향을 주지 않음) 생략할 수 있으며, 모델이 학습하면서 최소화해야 할 부분은 KLD 식의 앞부분인 크로스 엔트로피이다. 그러나 생성적 적대 신경망(GAN)에서는 실제 데이터를 모방하기 위해 생성된 분포가 매우 정확해야 하므로 이 정보가 중요하다. 이 때문에 GAN의 증명 과정에서는 KLD를 직접 사용하기보다는 KLD를 거리 개념으로 해석할 수 있는 Jensen-Shannon divergence를 활용하여 두 분포 간의 유사성을 평가하고 최적화 과정을 수행한다.
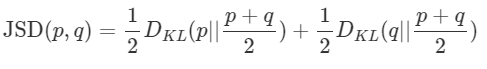
Jensen-Shannon Divergence는 우리가 일반적으로 생각하는 거리 개념을 만족하는 유사성을 측정하는 방법이다. 일반적으로 거리 AA와 BB 간의 거리는 AA를 기준으로 바라본 BB까지의 거리와 BB를 기준으로 바라본 AA까지의 거리가 같아야 한다. 그러나 KL-Divergence는 KLD(P∣∣Q)≠KLD(Q∣∣P)\text{KLD}(P || Q) \neq \text{KLD}(Q || P)로 정의되기 때문에 거리로 해석될 수 없다. 이로 인해 KLD는 비대칭적이며, 두 확률 분포 간의 유사성을 일관되게 나타내는 데 한계가 있다. 이에 비해 Jensen-Shannon Divergence는 이러한 비대칭성을 극복하여 두 분포 간의 대칭적인 거리를 제공함으로써, 더 직관적으로 해석할 수 있는 유용한 지표가 된다.
Probabality
Likelihood (가능도, 우도)
- 입력으로 주어진 확률 분포(파라미터)가 얼마나 데이터를 잘 설명하는지 나타내는 점수
* 데이터를 잘 설명한다 -> 해당 확률 분포에서 높은 확률 값을 가지는 것을 의미한다.
어떠한 현상에 있어 확률 변수 x와 x의 확률의 곱의 합이 가능도가 된다.
그러나 우리는 확률의 곱이 무수히 시행되면 그 값이 작아지게 되고 ( 분모가 무한대로 커지므로 ) 컴퓨터의
덧셈 연산의 장점을 위해 , 우도를 출력하는 함수에 log를 씌워서 log-likelihood로 변경한다.

세타라는 파라미터를 가진 분포에서 x_i의 확률과 x_i들을 곱한 값의 합 = 우도
그렇다면 우리가 해야할 일은 위에 있는 log-likelihood를 가장 최대화 하는 세타θ 를 찾아야한다.
이때 어떠한 log-likelihood를 우도함수라고 한다면 이 함수는 위로 볼록한 함수이다.
이때 최적의 파라미터 θ 는 gradient ascent로 찾아내게 된다. (아래로 볼록한 함수가 아니기 때문에)
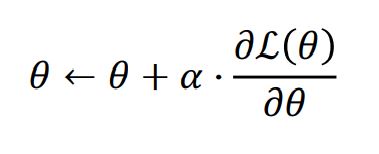
이 것을 우도를 최대한으로 하는 추정방법이라 하여 MLE(Maximum Likelihood Estimation)라고 하는데
딥러닝의 관점에서 대부분의 딥러닝은 Gradient Descent를 지원하기 때문에 minimization 문제가 되고
이를 위해 기존의 log-likelihood 에서 -를 붙여준 NLL(negative log-likelihood)가 되는 것이다.
또한 Gradient를 구하기 위해 log를 통해 곱셈의 문제를 덧셈으로 바꿔주면서 더 쉽게 미분이 가능하도록한다.
즉 딥러닝 관점에서, 분포 P(x)로 부터 샘플링한 데이터 x가 주어졌을때, 파라미터θ 를 갖는 신경망은 조건부 확률 분포를 나타낸다.
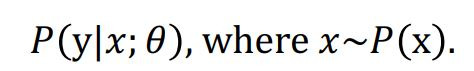
이때 Gradient Descent를 통해 NLL를 최소화하는 θ를 찾을 수 있게 된다.
신경망 역시 확률 분포 함수이기 때문에 MLE- > NLL의 과정을 통해 파라미터를 찾는 것이라고 볼 수 있다.
좀 더 수식의 관점에서 살펴보면
우리가 찾는 최적 파라미터는
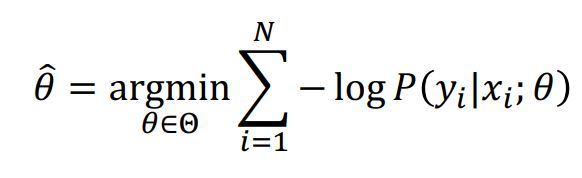
다음과 같으며,
이때 어떠한 확률분포 f(x) = f(y_iㅣx_i; θ)의 분포를
1) gausian distribution 2) bernoulli distribution
둘 중어느 분포로 가정하냐에 따라 위 손실함수는 MSE와 Cross-Entropy로 나뉘게된다.
이는 아래와 같이 실제 가우시안 분포와 베르누이 분포에 식을 전개해보면 알 수 있다.

출처 : https://www.youtube.com/watch?v=QfHcuPPW6W4&list=PLQASD18hjBgyLqK3PgXZSp5FHmME7elWS&index=6
즉 딥러닝의 대표 문제인 분류TASK에서 categorical한 분포를 가정하여 cross-entropy를 최소화하는 것을 MLE 관점으로 볼 수 있는 것이다.
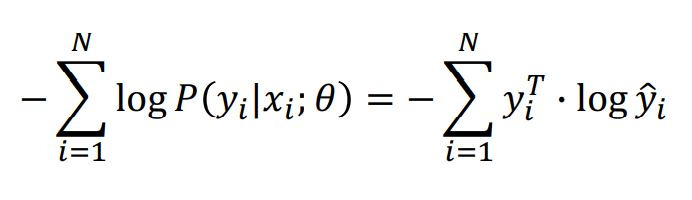
좌: NLL 우: CE
* 이때 보여지는 우변의 y_i는 one-hot encoding의 상태이기 때문에 [0,0,1,0,0,0..] 의 형태를 가지고
y_hat은 좌변의 P(y_iㅣx_i; θ)와 같다.
MLE
최대 우도법(MLE)은 주어진 데이터에 대해 가장 적합한 확률 모델의 매개변수를 찾는 방법으로, 특정 매개변수 하에서 관측된 데이터가 발생할 확률을 의미하는 우도(likelihood)를 최대화하는 것을 목표로 한다. 데이터가 독립적이라고 가정할 때, 각 데이터의 확률을 곱해 우도를 계산하지만, 이 과정에서 발생할 수 있는 underflow 문제를 피하기 위해 log를 취하여 log-likelihood를 사용한다. 이는 log 함수가 단조 증가(monotonic increase)하기 때문에 log-likelihood를 최대화하는 것이 원래의 likelihood를 최대화하는 것과 동일하기 때문이다.
왜 딥러닝이 MLE일까?
선형 회귀(linear regression), 이진 분류(binary classification), 다중 분류(multi classification)를 서로 다른 문제로 보기보다는 예상하는 분포의 차이로 이해해야 한다. 예를 들어, 선형 회귀는 연속적인 출력 변수를 예측하는데, 이 경우 목표는 주어진 입력에 대한 출력 값이 정규 분포를 따른다고 가정하는 것이다. 반면, 이진 분류는 두 개의 클래스를 구분하는 문제로, 로지스틱 회귀를 사용하여 각 클래스의 확률을 모델링하고 이진 분포를 따른다고 볼 수 있다. 다중 분류의 경우, 여러 클래스 중 하나를 선택하는 문제로, 소프트맥스 회귀(softmax regression)를 통해 각 클래스에 대한 확률을 계산하고, 다항 분포(multinomial distribution)를 따른다고 할 수 있다. 따라서, 이 세 가지는 결국 입력 데이터를 통해 출력 변수를 예측하는 방식에서 각기 다른 확률 분포를 가정하는 것에 불과하다고 정리할 수 있다.
Linear regression
- Linear regression은 가우시안 분포의 평균이 likelihood라고 "가정"해보는 것입니다.
- 이 likelihood를 최대화하는 것이 목표일 것입니다.
- -log를 붙여서 loss 함수로써 사용하는 것입니다!!
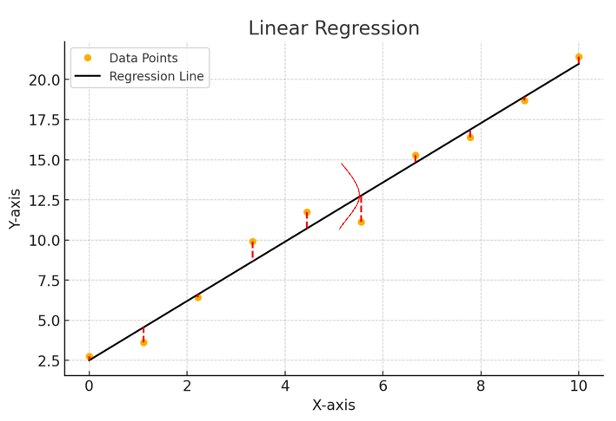
(그림이 이상한 점 이해 부탁드립니다..)
- 수학식으로 표현하자면 다음과 같습니다.
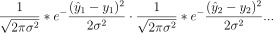
여기에 -log를 취해주면,
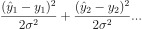
다음과 같이 된다.
즉, linear regression 에서는 MSE라는 loss 함수가 자연스레 도출됩니다.
Binary classification
- 이진 분류는 binomial 분포를 likelihood라고 "가정"해보는 것입니다.
- 결국은 0이거나 1인 것이기 때문에 동전 뒤집기라고 생각하면 쉽게 이해가 가능할 것입니다.
- 수학 식으로 표현하면 다음과 같다
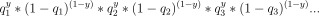
해당 식에 -log를 취해주면, -ylogq 들의 합으로 표현될 수 있고, 이것을 minimum 하는 것이 원래의 식을 maximum 하는 것과 같다. 이 식이 BCE, Binary Cross Entropy 라고 볼 수 있다.
Multi Classification
- 다중 분류는 multinomial 분포를 likelihood라고 "가정"해보는 것입니다.
- 만약 개, 고양이, 소 3개의 동물을 분류한다고 가정해봅시다.
- 그렇다면 loss는 다음과 같습니다.
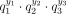
- 여기에 -log를 취하면,
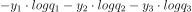
다음과 같습니다.
one-hot encoding으로 분류를 진행할 때, 만약 y1이 개라면, 예상 값 [q1,q2,q3]에 대해 개를 정확히 예측하여 [1,0,0]라고 했다면, loss는 0일 것이다. 고양이와 소에도 마찬가지로 loss는 0일 것이다.
즉, loss는 0보다 크거나 같은 값이다.
해당 loss가 바로 cross-entropy이다.
이렇게, 딥러닝에서 weight를 업데이트하기 위한 loss들이 갑자기 툭 튀어나온 것이 아니라, 분포를 가정하여 나온 것을 확인할 수 있습니다. 결국 딥러닝이란 이러한 가능도(likelihood)를 최대화하는 것이 목표이다.
- 세그멘테이션 연구를 진행할 때 사용한 Dice loss는 평가 지표은 Dice Score를 loss로 활용한 것이기 때문에 어떠한 분포를 가정할 수는 없다고 생각한다.
'Artificial Intelligence > Artificial Intelligence Theory' 카테고리의 다른 글
| Deep Learning [3] : 트랜스포머 (Transformer) (0) | 2024.11.28 |
|---|---|
| Deep Learning [2] : 시계열 데이터 신경망 모델 (Time Series Data Learning Models) (1) | 2024.11.12 |
