
해당 논문은 Leap Motion의 핸드 트레킹과 Unity의 물리 엔진을 결합하여 사용자가 미세 중력의 가상 환경에서 손으로 객체를 조작하는 몰입감 있는 상호작용을 제공하는 연구이다. Leap Motion은 손의 위치, 속도, 회전 데이터를 실시간으로 추적하며, Unity의 물리 엔진은 충돌 감지, 접촉 지점 계산, 임펄스와 마찰력 적용을 통해 현실감 있는 물리적 반응을 시뮬레이션한다. 또한, 노이즈 필터링 기법을 적용해 손의 움직임을 안정적으로 처리하며, 사용자가 가상 객체를 잡고, 이동하며, 놓는 등의 섬세한 상호작용을 수행할 수 있도록 설계되었다. God Object 접근법을 사용하여 손이 가상 객체를 뚫고 지나가는 문제를 해결하고, 손과 객체 간의 접촉을 유지하며 자연스러운 시각적 피드백을 제공한다. 이를 통해 시스템은 물리적 정밀성과 시각적 일관성을 갖춘 미세 중력의 가상 환경을 구현해낸다.
1. 논문 분석
선행 연구

1. 접촉 감지 (Collision Detection)
가상 손이 객체와 접촉했는지 확인하려면, 손과 객체의 표면 지점 간의 거리를 계산한다. 접촉이 발생하면 접촉점에서의 법선 벡터(n)와 변위(δ)를 기반으로 물리적 상호작용을 계산한다. 접촉 조건은 다음과 같이 표현된다:
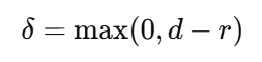
- : 손과 객체의 표면 사이의 거리.
- : 접촉 임계값(객체의 반경 등).
손가락 끝이 공에 가까워지는 상황을 가정하자. 손가락과 공 표면 사이의 거리가 d = 0.5 cm이고, 접촉 임계값 r = 0.3라면: δ=0.5−0.3=0.2 cm로 이 경우 손이 공과 접촉했다고 간주한다.
2. 반발력 계산 (Normal Force)

접촉이 발생하면, 손이 객체에 가한 힘(정상력, f_n)을 계산한다. 이 힘은 접촉 강성(k)과 변위(δ)에 따라 결정된다:
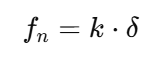
- : 접촉 강성(객체의 재질 특성을 반영)
- δ: 접촉 변위(손이 객체를 누른 정도)
손가락 끝으로 공을 살짝 누른 경우를 생각하자. 접촉 강성이 k=1000 이고, 변위가 δ=0.001 m라면, fn=1000×0.001=1N, 손가락은 공을 1N의 힘으로 누르게 된다.
3. 마찰 모델링 (Friction Force)
마찰력은 손이 객체를 유지하거나 움직이려고 할 때 발생하며, 정적 마찰과 동적 마찰로 나뉜다. 마찰력은 정상력(fn)과 마찰 계수(μ)를 이용해 계산된다.
정적 마찰:

- ft: 마찰력.
- μs: 정적 마찰 계수.
동적 마찰:
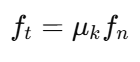
- μk: 동적 마찰 계수.
손으로 공을 잡고 있다가 움직이려고 할 때, 공의 표면과 손 사이의 정적 마찰 계수 μs=0.4, 정상력 fn=1,이라고 가정하자 ftmax=0.4×1=0.4N 손이 0.4N 이상의 힘을 가하면 공이 움직이기 시작하며 이후 동적 마찰력이 적용된다. 만약 동적 마찰 계수가 μk=0.3이라면 ft=0.3×1=0.3 N 공이 움직이는 동안 마찰력은 0.3N으로 일정하게 유지된다.
4. 요약
요약 : 먼저, 손가락 끝이 공에 가까워지면 시스템은 손과 공 표면 사이의 거리를 계산해 접촉 여부를 판단한다. 손가락 끝과 공 표면 사이의 거리가 0.5 cm이고, 접촉 기준 거리(임계값)가 0.3 cm라면, 접촉이 발생했다고 간주한다. 접촉 지점에서는 공 표면의 변위(δ)를 0.2 cm로 계산한다. 이후, 접촉 변위를 기반으로 손이 공에 가하는 반발력을 계산하는데, 공의 접촉 강성()이 1000 N/m일 경우, 반발력은 fn = k⋅δ = 1000 ⋅ 0.002 = 2N이 된다. 이 반발력은 공이 손가락을 밀어내는 힘으로 작용하며, 공의 안정적인 접촉 상태를 유지하게 된다.
다음으로, 손가락이 공을 잡고 들어 올리려 할 때 마찰력이 작용한다. 손과 공 사이의 마찰 계수는 정적 마찰 계수(μs)로 0.5라고 가정한다. 이때 정상력(fn)이 2N이므로, 최대 정적 마찰력은 ftmax=μs⋅fn=0.5⋅2=1N이 된다. 손가락이 가로 방향으로 1N이하의 힘을 가하면 공은 손에 고정되지만, 이를 초과하면 공이 미끄러지며 동적 마찰력이 적용된다. 동적 마찰 계수(μ)가 0.3이라면 동적 마찰력은 ft = μk ⋅ fn = 0.3 ⋅ 2 = 0.6N로 유지된다. 이 과정에서 시스템은 손과 공의 위치, 접촉 상태, 힘의 방향 등을 기반으로 에너지 함수 E total = E deformation + E contact를 계산하고 이를 최소화한다.
예를 들어, 공이 손가락 끝에서 자연스럽게 회전하거나 위치를 변경하려면, 시스템이 접촉 지점에서의 변형 에너지와 접촉 에너지를 동기화해 가상 손이 실제 손처럼 행동하도록 업데이트한다. 이러한 과정을 통해 손은 공을 잡고, 들어 올리고, 움직이며, 안정적으로 놓는 등의 복잡한 물리적 상호작용을 구현할 수 있다. 이는 사용자가 가상 환경에서 실제로 공을 조작하는 듯한 직관적이고 몰입감 있는 경험을 제공한다.
5. 한계
첫 번째 논문의 반발력 계산은 접촉 변위와 접촉 강성을 기반으로 하며, 이는 객체가 안정적으로 고정된 환경에서 적합하다. 그러나 미세중력 환경에서는 물체가 쉽게 움직이고 가속될 수 있기 때문에 충격 기반 상호작용(impulse-based interaction)을 포함하지 않으면, 접촉 순간의 빠른 운동 변화나 물체의 예측 불가능한 반응을 적절히 모델링할 수 없다. 예를 들어, 미세중력에서는 공이 손가락 끝과 접촉할 때, 반발력만으로는 공이 느끼는 가속도를 제어하기 어렵다. 타겟 논문은 이를 개선하기 위해 충격 기반 시뮬레이션을 도입해 문제를 해결한다.
또한 정적 마찰과 동적 마찰을 중력 환경에서의 정상력을 기반으로 계산했다. 정상력은 중력 가속도()에 크게 의존하며, 미세중력에서는 g≈0으로 인해 마찰력 계산이 무의미해진다. 이로 인해 미세중력 환경에서 손이 객체를 잡거나 움직이려 할 때의 동작을 제대로 표현하지 못한다. 타겟 논문은 이러한 마찰 모델의 한계를 인식하고, 관통 접촉 동역학(penetration contact dynamics)을 통해 접촉 영역에서 발생하는 힘과 운동을 더 정밀하게 모델링한다.
2. 타겟 논문 구현
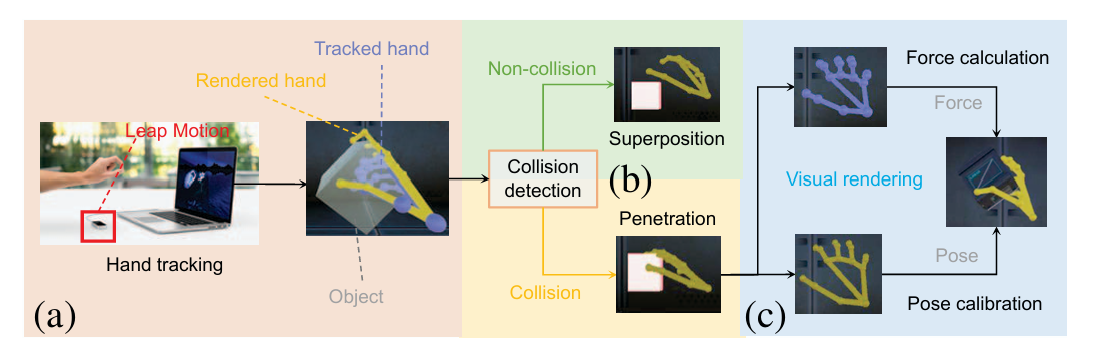
1. Handtracking Module


손의 움직임 추적 및 데이터 수집
핸드 트래킹 모듈은 Leap Motion 디바이스를 사용해 작동한다. 이 디바이스는 사용자의 손과 손가락 움직임을 3D로 실시간 추적하며, 손의 위치와 방향 데이터를 수집한다. 이 데이터는 손의 골격 구조(손가락 5개, 손바닥, 손목)를 바탕으로 가상 환경에서 손의 움직임을 재현하는 데 사용된다.
노이즈 필터링
미소중력 환경에서는 중력이 없기 때문에 작은 방해 요소나 노이즈가 손-물체 상호작용에 더욱 큰 영향을 미친다. 필터링되지 않은 상태에서는 움직임이 불규칙하고 물체 조작이 어렵다. 이를 위해 윈도우 필터링 기법을 도입했다. 이 방법은 손 움직임 데이터를 부드럽게 처리해 노이즈를 억제하고, 동시에 시스템 반응성을 유지하도록 설계되었다. 필터링 과정은 다음과 같은 수식으로 표현된다:
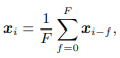
여기서 F는 필터 윈도우 크기를 나타내며, 필터링의 강도를 조절한다. 가 너무 작으면 노이즈 제거 효과가 충분하지 않고, 너무 크면 시스템의 반응 속도가 느려진다. 실험을 통해 F=3이 가장 적합한 값으로 선택되었으며, 이는 노이즈 억제와 실시간 반응성의 균형을 유지한다.
논문에서는 Window Average Filter를 사용했지만, 몇 가지 단점들을 파악하고 이를 개선점으로 삼았다. 먼저 Window Average Filter 모든 데이터를 동일한 가중치로 처리하기 때문에 손의 움직임에서 발생하는 급격한 변화를 희석시킨다. 이는 중요한 에지 정보를 손상시켜 정밀한 핸드 트래킹이 요구되는 환경에서 부정확한 결과를 초래할 수 있다. 그리고 이상치(outlier)에도 민감하다. 손의 위치 데이터에 이상치가 포함되면 평균값에 영향을 미쳐 잡음이 제거되지 않거나 오히려 증가할 수 있다. 마지막으로 필터링 과정에서 일정 범위의 과거 데이터를 참조해야 하므로 윈도우 크기가 클수록 지연시간이 늘어나 실시간 응답성이 저하된다.
이러한 한계를 원유로 필터(Wiener Filter)를 사용함으로써 개선하고자 했다. 원유로 필터는 신호와 잡음의 통계적 특성을 기반으로 동적으로 가중치를 조정하여, 신호의 중요한 변화를 더 잘 보존한다. 이는 단순 평균값에 의존하는 윈도우 에버리지 필터와 달리, 신호와 잡음을 효과적으로 분리할 수 있도록 설계되었기 때문이다. 또한, 원유로 필터는 이상치나 비정상적인 데이터에 덜 민감하다. 데이터의 분산 정보를 활용하여 이상치로 인한 왜곡을 최소화하면서 부드럽고 정확한 데이터를 생성한다. 더불어, 원유로 필터는 신호 대 잡음비(SNR)를 최적화함으로써, 윈도우 에버리지 필터보다 우수한 필터링 품질을 제공한다. 이는 핸드 트래킹과 같은 실시간성이 중요한 환경에서 특히 유용하며, 손의 미세한 움직임이나 복잡한 제스처를 보다 정확하게 추적할 수 있다. 이러한 장점으로 원유로 필터로 필터링 방식을 대체해 기존 단점을 보완하고, 더 나은 추적 성능과 사용자 경험을 제공하고자 했다.
OneEuroFilterUnity/Assets/Scripts/OneEuroFilter.cs at main · DarioMazzanti/OneEuroFilterUnity
OneEuroFilter utility for Unity. Contribute to DarioMazzanti/OneEuroFilterUnity development by creating an account on GitHub.
github.com
[Header("Joints to Filter")]
public List<Transform> jointTransforms; // 손가락 조인트들의 Transform 목록
[Header("OneEuroFilter Parameters")]
public float freq = 90.0f; // 업데이트 주파수 (Leap Motion은 약 90Hz)
public float minCutoff = 0.1f; // 최소 컷오프 주파수
public float beta = 0.05f; // 속도에 따른 반응도 조정
public float dCutoff = 1.0f; // 변화율에 대한 컷오프 주파수
// 각 조인트에 대응하는 OneEuroFilter 인스턴스
private Dictionary<Transform, OneEuroFilter<Vector3>> jointFilters;
void Start()
{
// 각 조인트에 대해 OneEuroFilter 초기화
jointFilters = new Dictionary<Transform, OneEuroFilter<Vector3>>();
foreach (Transform joint in jointTransforms)
{
jointFilters[joint] = new OneEuroFilter<Vector3>(freq, minCutoff, beta, dCutoff);
}
}
2. Collision Detection and God Object
손과 물체 간 상호작용에서 충돌 감지를 통해 추적된 손이 가상 객체를 관통하거나 겹치는 일이 발생하지 않도록 한다. 이를 구현하기 위해 두 가지 손 모델, 즉 추적된 손(Tracked Hand)과 렌더링된 손(Rendered Hand)이 사용된다. 추적된 (Tracked Hand)은 실제 사용자의 손을 가상 환경에서 그대로 반영한 모델로 사용자의 손 움직임과 위치를 정확히 모방하여 물리적 세계와 가상 세계 사이의 원활한 통합을 보장한다. 반면, 렌더링된 손(Rendered Hand)은 사용자가 가상 객체와 상호작용할 때 손 움직임을 자연스럽고 시각적으로 매력적으로 표현하여 사용자 경험을 향상한다. 이 두 모델은 현실감을 높이고 몰입감 있는 상호작용을 제공한다.
충돌 감지 과정은 추적된 손의 위치와 방향을 가상 객체의 기하학적 형태와 비교하여 충돌이 발생했는지 확인한다. 충돌이 다수의 접촉 지점에서 발생할 수 있지만, 각 접촉 지점의 단일 충돌(Single-Point Collision)을 독립적으로 계산하는 것이 중요하다. 예를 들어, 손가락 끝이 가상 상자 모서리에 닿는 상황을 생각할 수 있다. 이 경우, 접촉 지점에서의 접촉 정상 벡터(Contact Normal Vector)를 계산한다.
연속적이고 매끄러운 표면을 가진 물체라면, 접촉 지점에서의 표면 정상 벡터가 두 물체(손과 가상 객체)의 표면 정상 벡터와 평행하지만 반대 방향으로 정렬된다. 예를 들어, 손바닥이 매끄러운 구체에 닿는 상황을 상상할 수 있다. 손이 구체의 표면에 접촉하면 구체의 표면 정상 벡터가 접촉 지점을 기준으로 반대 방향으로 나가면서 손의 표면 정상 벡터와 평행하게 된다.
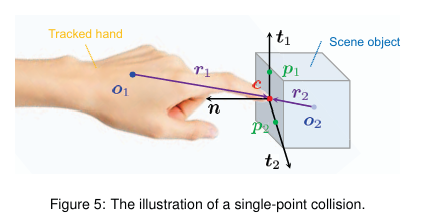
1) 접촉 지점의 계산
추적된 손과 가상 객체가 서로 접촉한 지점을 계산하기 위해 두 객체의 중심 위치와 접촉 지점까지의 벡터를 이용한다. 예를 들어, 손의 중심 위치를 o1=(0,0,0로 하고 접촉 지점까지의 벡터를 r1=(1,0,0)라고 하자. 마찬가지로 가상 객체의 중심 위치를 o2=(0,1,0)로, 접촉 지점까지의 벡터를 r2=(−1,0,0)로 설정한다. 접촉 지점은 다음과 같이 계산된다:
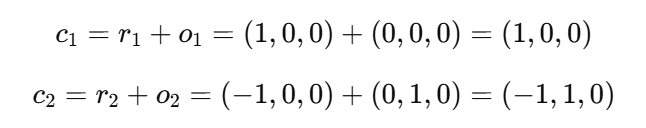
접촉이 발생하려면 두 지점이 동일해야 한다. 위의 예에서 c1과 c2는 서로 다르므로, 추가적인 조정이나 확인이 필요하다.
2) 회전 행렬을 이용한 접촉 지점 표현
손과 객체가 움직이거나 회전할 때, 각 객체의 기준 좌표계(body frame)에서 접촉 지점을 계산해야 한다. 기준 좌표계에서의 벡터는 다음과 같이 회전 행렬 RiR_i를 사용해 변환한다.
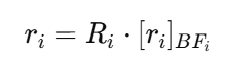
예를 들어, 손의 회전 행렬이 단순한 90도 회전을 나타낸다고 가정하자. 이 경우:
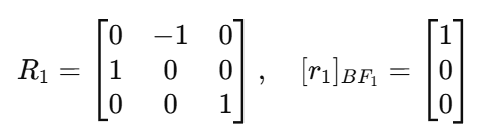
회전 행렬을 적용하면:
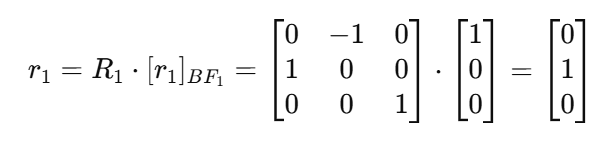
이렇게 계산된 r1r_1은 접촉 지점을 구하는 데 사용된다.
3) 접촉 지점의 속도 계산
접촉 지점의 속도는 물체가 시간에 따라 어떻게 움직이는지를 나타내며, 이는 회전과 병진 운동을 포함한다. 접촉 지점의 속도는 다음 식으로 계산된다
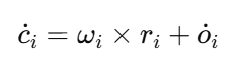
여기서 ωi는 각속도, ri는 접촉 지점까지의 벡터, o˙i는 객체 중심의 선형 속도이다. 예를 들어, 손의 각속도가 ω1=(0,0,1)이고 r1=(1,0,0)라고 하자. 선형 속도는 o˙1=(0,1,0)라고 가정한다. 접촉 지점의 속도는 다음과 같이 계산된다
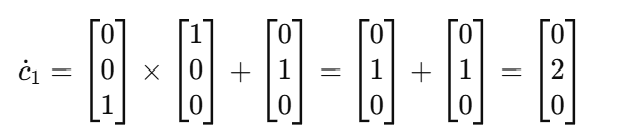
따라서, 접촉 지점의 속도는 (0,2,0)이 된다. 이는 손이 객체와 상호작용할 때 실제로 어떤 속도로 움직이는지를 나타낸다. 이 과정에서 사용자가 오브젝트를 밀 때, 속도와 회전 정보를 기반으로 오브젝트의 움직임을 정확히 예측할 수 있다.
4) 접촉 지점의 속도 계산
접촉 지점에서 손과 가상 객체 간의 상대적인 움직임을 평가하기 위해, 접촉 속도 vv를 계산한다. 이 속도는 접촉 지점에서 두 물체가 어떻게 움직이는지를 나타낸다. 상대 접촉 속도는 다음과 같은 수식으로 정의된다
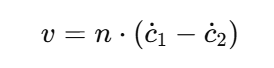
- n은 접촉 지점의 정상 벡터(normal vector)로, 접촉 표면에서 수직 방향을 나타낸다.
- c˙1과 c˙2는 각각 추적된 손과 가상 객체의 접촉 지점 속도를 나타낸다.
이 값을 통해 접촉 상태를 다음과 같이 분류할 수 있다:
- v>0: 분리 접촉(Separating Contact)
접촉 지점에서 두 물체가 서로 멀어지고 있다. 이 경우, 앞으로의 시뮬레이션에서 두 물체는 접촉을 유지하지 않는다. - v=0: 정지 접촉(Rest Contact)
두 물체가 접촉 상태를 유지하고 있으며, 접촉 지점은 변하지 않는다. - v<0: 충돌 접촉(Colliding Contact)
두 물체가 서로 충돌하고 있으며, 아무 조치도 취하지 않으면 접촉 지점에서 관통이 발생할 가능성이 있다. 이 경우, 충돌 임펄스를 적용해 상호작용을 조정해야 한다.
5) God - Object
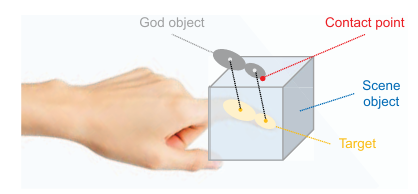
God-Object 접근법은 접촉 지점 업데이트와 관통 문제를 해결하기 위해 사용된다. 이 방법에서는 가상 객체를 단일한 독립적 실체로 간주하며, 손과 객체의 상호작용을 기반으로 접촉 지점을 동적으로 조정한다. 주요 특징은 다음과 같다:
- 렌더링된 손과의 상호작용
렌더링된 손은 객체와의 시각적 상호작용을 담당하며, 사용자가 손으로 객체를 조작할 때 자연스러운 피드백을 제공한다. - 각 손가락 관절과의 연결
추적된 손의 각 손가락 관절(마디)은 대상 객체와 연결된다. 관절마다 "God-Object"로 표현된 독립된 접촉 지점을 가지며, 이를 통해 세밀한 조작이 가능하다. - 시뮬레이션 정확성
접촉 지점의 깊이와 객체의 동역학을 고려하여 정확한 시뮬레이션을 수행한다. 예를 들어, 손가락이 물체를 누르거나 미는 상황에서 접촉 깊이를 기반으로 힘을 조절한다.
6) 요약
손과 가상 객체의 상호작용을 현실적으로 구현하려면, 두 물체가 서로 어떻게 움직이는지를 정확히 파악해야 한다. 이를 위해 접촉 지점에서 손과 가상 객체의 상대적인 움직임을 계산하고, 충돌 여부를 판단하며, 이를 처리하는 과정을 거친다. 접촉 지점에서의 상대 속도는 손이 물체를 밀거나, 잡거나, 놓는 동작을 모델링하는 데 중요하다. 예를 들어, 사용자가 손으로 가상 공을 잡고 있다가 공을 위로 들어 올린다고 가정해보자. 손이 공의 표면에서 멀어지면, 두 물체는 분리 상태에 있게 된다. 반대로, 손이 공을 누르거나 밀고 있다면 두 물체는 서로 접촉하면서 영향을 주고받는다. 이렇게 손과 물체가 서로 어떤 방향으로 움직이고 있는지를 이해하면, 공이 어떤 방식으로 반응해야 하는지를 자연스럽게 결정할 수 있다.
충돌 상태는 크게 세 가지로 나뉜다. 첫째, 손이 물체와 멀어지면 접촉이 끊어지는 분리 상태다. 이 경우, 공은 더 이상 손의 영향을 받지 않고 원래 위치에서 자유롭게 유지된다. 둘째, 손과 물체가 접촉하지만 움직임이 없는 정지 상태다. 예를 들어, 손바닥 위에 공이 가만히 놓여 있는 상황이 이에 해당한다. 셋째, 손이 물체를 더 깊이 누르거나 밀어 물체에 영향을 주는 충돌 상태다. 이 경우, 공은 손의 힘을 받아 움직이거나 회전하게 된다.
God-Object 접근법은 충돌 상태를 보다 현실적으로 처리하기 위한 방식이다. 예를 들어, 사용자가 손가락으로 얇은 막대기를 잡으려고 한다고 가정하자. 손가락이 막대기를 관통하면, 시각적으로는 손가락이 막대기의 표면 위에 있는 것처럼 보이도록 조정한다. 사용자가 손가락으로 막대기를 누르면, 막대기는 손가락이 가하는 힘과 방향에 따라 움직인다. 이를 통해 사용자는 막대기를 실제로 잡고 움직이는 것 같은 경험을 하게 된다.
손이 물체를 단순히 잡는 상황을 넘어, 물체 표면을 따라 문지르거나 회전시키는 동작에서도 접촉 지점은 계속 변화한다. 예를 들어, 사용자가 손바닥으로 공을 굴린다면, 공의 표면과 손바닥의 접촉 지점은 공의 움직임에 따라 끊임없이 변한다. 이 접촉 지점을 동적으로 계산함으로써 공이 실제로 굴러가는 것처럼 보이고 느껴지도록 만든다. 이는 단순히 충돌을 감지하는 것을 넘어, 움직임과 힘의 변화를 실시간으로 반영해 자연스러운 상호작용을 가능하게 한다.
3. Interaction Relationship Reasoning
이후, Interaction Relationship Reasoning 단계가 시작된다. 이 단계에서는 손과 공 사이의 접촉 이후의 동작을 물리적으로 시뮬레이션한다. 만약 손이 공을 단순히 건드리고 있다면, 충격량(impulse)이 계산되고, 공은 약간 튕겨 나가는 움직임을 보일 것이다(Impulse Phase). 이때 사용자의 손이 강하게 밀었다면, 공은 더 멀리 이동하거나 빠르게 회전할 수 있다. 반면, 손이 공을 잡고 유지하려는 경우에는 관통 접촉 역학(Penetration Phase)이 활성화된다. 이 단계에서는 손과 공이 접촉 상태를 유지하도록 마찰력(friction)과 안정성(stability)을 계산하며, 공이 손에서 미끄러지지 않도록 한다.
이를 해결하기 위해, 충격 기반 접근법(impulse-based method)과 관통 접촉 역학(penetration contact dynamics)을 결합한 방식을 제안한다. 충격 기반 접근법은 충돌 시 물체 간의 충격 교환과 운동량 변화를 시뮬레이션하는 데 초점을 맞추며, 관통과 분리 개념에만 의존하지 않는다. 이를 통해 손과 물체 간의 운동량 및 힘의 전달을 보다 정밀하게 재현하여 미소중력 환경에서 미세한 상호작용을 시뮬레이션할 수 있다.
1) The Impusle Phase
사용자가 가상 환경에서 손으로 공을 강하게 밀었다고 가정한다. 이때 공은 손의 힘을 받아 일정한 속도로 움직이며, 충돌 시 초기 반응이 중요한 역할을 한다. 이를 기반으로 각 단계를 설명한다.
(1) 충돌 충격량 계산 (Collision Impulse Calculation)
충격량은 접촉 지점의 법선 방향(normal direction)을 따라 작용한다고 가정하며, 이 법선 방향은 접촉 표면의 수직 벡터로 정의된다. 예를 들어, 사용자가 손으로 공을 강하게 밀었다면, 손과 공의 접촉 지점에서 수직 방향으로 충격량이 작용하게 된다. 충격량 는 접촉 지점의 법선 방향(normal direction)과 평행하다고 가정한다. 이로 인해 충격량은 다음과 같이 표현된다

여기서 j는 충격량의 크기(magnitude), 은 접촉 지점에서의 법선 벡터이다.
(2) 뉴턴의 충돌 법칙 (Newton’s Collision Law)
충돌이 발생하면, 공의 초기 상대 속도(uinit)와 최종 상대 속도(ufinal)는 복원 계수(ϵ)따라 결정된다. 복원 계수는 충돌의 탄성을 나타내며, ϵ=0이면 비탄성 충돌로, ϵ=1이면 완전 탄성 충돌로 정의된다. 이 관계를 통해 상대 속도의 변화량(Δu)을 계산할 수 있다. 예를 들어, 초기 속도가 2 m/s이고 복원 계수가 0.5라면, 최종 속도는 −1 m/s가 되며, 상대 속도 변화량은 −3 m/s이다. 뉴턴의 충돌 법칙에 따르면, 초기 상대 속도 ui와 최종 상대 속도 ufinal 사이의 관계는 다음과 같다
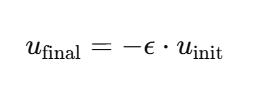
여기서 ϵ은 법선 복원 계수(normal restitution coefficient)로, 값은 에서 1 사이이다. 이 계수는 충돌의 탄성을 측정하며, 0에 가까울수록 충돌이 비탄성적이고, 1에 가까울수록 완전히 탄성적이다.
(3) 속도 변화 계산
상대 속도의 변화량 Δu는 다음과 같이 계산된다:
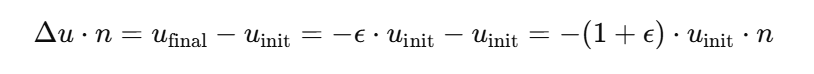
이는 충돌 시 상대 속도가 얼마나 감소하거나 반전되는지를 나타낸다.
(4) 운동량 관계 (Impulse-Momentum Relationship)
운동량 변화량과 충격량은 물리적으로 연결되어 있다. 충격량의 크기()는 물체의 질량과 속도 변화에 따라 결정된다. 여기서 K는 물체의 충돌 행렬로, 물체의 질량과 충돌 특성을 반영한다. 만약 공의 질량이 1 kg이고, 초기 속도와 복원 계수에 따라 계산된 충격량 j가 −3 Ns라면, 이 충격량은 공의 선속도를 변화시키는 데 사용된다. 운동량 변화량과 충격량 사이의 관계는 다음과 같다.
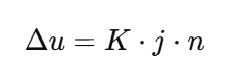
여기서 K는 충돌 행렬(collision matrix)로, 물체의 질량(mass)과 물리적 특성에 따라 결정된다.
법선 방향에서의 속도 변화는 다음과 같이 계산된다:
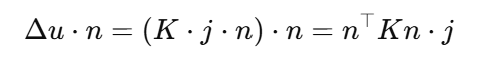
(5) 충격량 계산
위의 식을 정리하여 를 다음과 같이 계산한다:
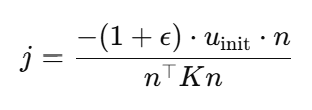
이 식은 초기 속도, 복원 계수, 충돌 행렬을 기반으로 충격량의 크기를 계산한다.
(6) 충격량 적용 (Applying the Impulse)
충격량이 적용되면 공의 선속도는 충격량과 공의 질량에 의해 변한다. 예를 들어, 공의 질량이 1 kg이고 충격량이 −3Ns라면, 공의 속도 변화는 −3 m/s가 된다. 이를 통해 공은 초기 상태에서 반대 방향으로 새로운 속도를 가지며 움직이게 된다. 이 과정은 충돌 순간의 초기 반응을 정밀하게 계산하여, 미소중력 환경에서도 현실적인 물리적 움직임을 시뮬레이션할 수 있도록 한다. 결과적으로, 사용자는 실제 물체를 다루는 것처럼 자연스럽고 몰입감 있는 상호작용을 경험할 수 있다. 충격량 J는 가상 물체에 적용되어 물체의 선속도(linear velocity)가 변한다. 속도 변화량은 다음과 같이 계산된다:
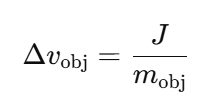
여기서 mobj는 가상 물체의 질량이다.
이를 통해 물체의 새로운 운동 상태(선속도 및 방향)를 다음과 같이 얻을 수 있다:
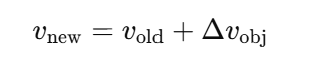
요약 : Impulse Phase는 충돌 순간에 물체가 어떤 반응을 보이는지를 시뮬레이션하는 과정이다. 손이 공을 밀기 시작하면, 먼저 손과 공이 접촉하는 순간의 속도 변화가 발생한다. 이때 공은 손이 가한 힘에 따라 반응한다. 충격량(impulse)은 손이 공에 주는 "밀어내는 힘의 효과"라고 생각할 수 있다. 만약 손이 빠르게 공을 밀면, 공은 더 멀리, 더 빠르게 움직인다. 반대로, 손이 천천히 밀거나 약하게 밀면, 공은 짧은 거리만 움직인다. 충격량의 크기와 방향은 손의 움직임과 공의 특성(예: 질량)에 의해 결정된다.
충격량이 공에 적용되면, 공의 움직임이 달라진다. 예를 들어, 공이 원래 멈춰 있는 상태에서 손으로 강하게 밀면, 공은 손의 힘을 받아 빠르게 앞으로 움직이기 시작한다. 하지만 손이 공을 약하게 밀었다면, 공은 천천히 움직인다. 이러한 변화는 충격량이 공의 속도를 바꾸는 방식에 해당한다. 한편, 공이 이미 움직이고 있다면, 손이 미는 방향에 따라 속도가 더 빨라지거나 방향이 바뀔 수 있다.
이 과정은 충돌 순간의 물리적 상호작용을 직관적으로 재현한다. 손이 공을 밀었을 때 공이 어떻게 움직일지 결정하며, 공이 빠르게 튕겨 나가거나 천천히 굴러가는 움직임을 정확히 반영한다. 결국, 사용자는 실제로 손으로 공을 밀어보는 것처럼 자연스러운 상호작용을 경험할 수 있다. 이러한 방식은 특히 미소중력 환경에서 공이 튕기거나 움직이는 방식을 현실적으로 표현하는 데 중요한 역할을 한다.