3. Camera Models

Computer Graphics Camera Model
카메라 모델(Camera Model) : 디스플레이에 그래픽스를 표현하기 위해서는 카메라가 촬영을 할 때 카메라 안에서 어떤일이 벌어지는지를 이해하고 가상의 카메라를 모델링 할 수 있어야 한다.
1. Imaging Geometry
카메라 모델의 Imaging Geometry는 3D 공간의 물체를 2D 이미지 평면에 투영하는 과정을 4단계로 설명한다.

Imaging Geometry
Worlds Coords - Camera Coords = Rigid Transformation
Camera Coords - Film Coords = Perspective , Weak Perspective
Film Coords - Pixel Coords = Affine Transformation
1. World to Camera Transformation: 3D 공간에서 물체의 위치를 월드 좌표에서 카메라 좌표로 변환하는 과정으로 두 단계로 나눌 수 있다.
World to Camera Transformation Matrix
- Translate by - C(align origins): 카메라 좌표계의 원점을 월드 좌표계의 카메라 위치로 이동한다. 이 이동은 3D 공간에서 벡터를 이동하는 3x1 이동 벡터를 사용하여 수행된다.
- Rotate to align axes: 월드 좌표 축과 카메라 좌표 축을 일치시키도록 회전한다. 이 회전은 3D 공간에서 축을 회전하는 회전 행렬로 수행된다.
2.Camera to Film Transformation : 3D 공간의 점을 2D 평면에 투사하는 과정이다.

Pinhole
카메라는 물체를 정확하게 한곳에 모으기 위해 핀홀을 뚫어 필름에 상을 맺히도록 한다. 피사체와 핀홀의 거리가 10이고 핀홀과 필름의 거리가 1이라면, 이미지는 피사체의 10분의 1의 크기가 될 것이다. 이런 원리로 Film Coordinate로 변환하는 것을 적용하면 된다.
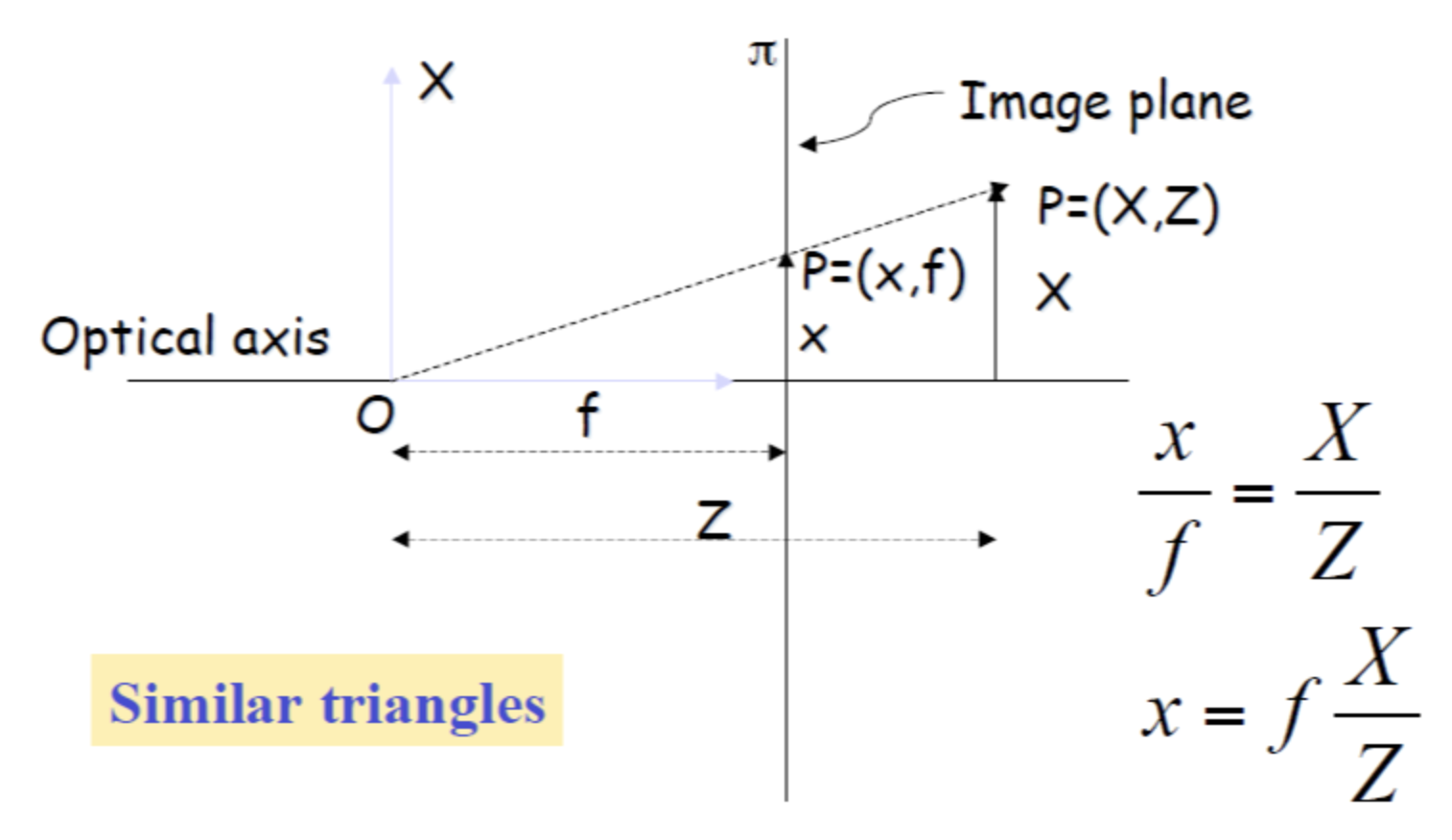
Pinhole Camera Model
P=(X,Z)는 피사체이며 P=(x,f)는 원래는 Optical axis글자의 왼쪽에 위치한 필름이지만, 그림이 길어지기에 오른쪽으로 대칭이동시킨 것이다. 따라서 공식을 유도하면 위의 비례식이 성립한다. 이미 X, Z는 알고 f는 카메라가 조정할 수 있기에 x값을 알 수 있다.
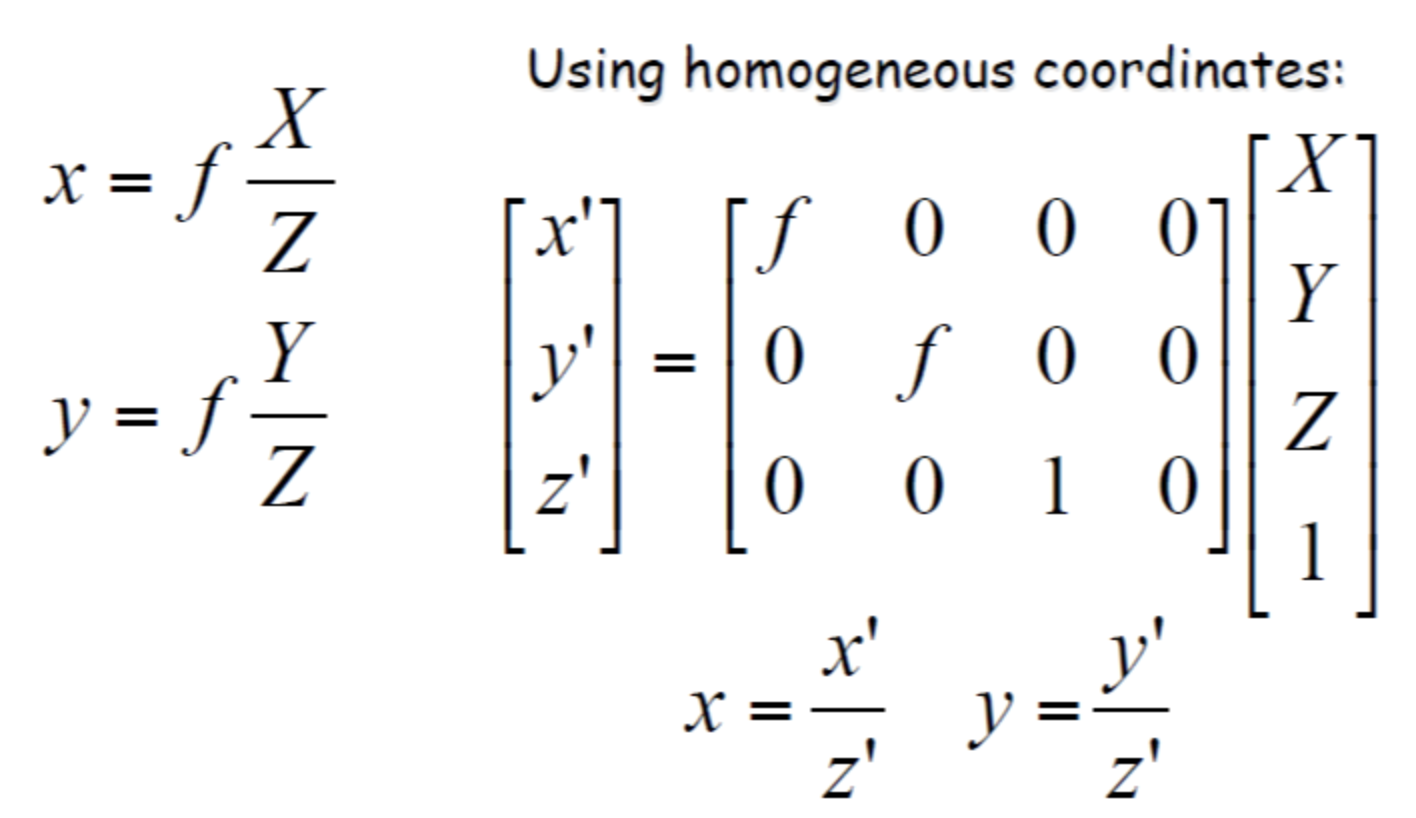
Perspective Matrix Equation
3. Film to Pixel Transformation : 필름의 좌표계를 우리가 흔히아는 JPG, PNG등 에서 사용하기 위해 픽셀 좌표계로 변환한다. 원래의 물체가 필름에 이렇게 있다고 하자.

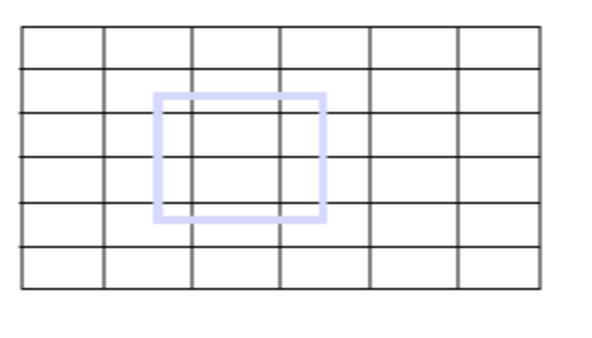
그런데 어떠한 카메라의 픽셀은 가로로 길쭉해서 오른쪽처럼 나올 수가 있다.
원래 물체는 세로로 길쭉했는데, 픽셀의 모양에 따라 가로로 늘어날 수가 있다는 의미이다.
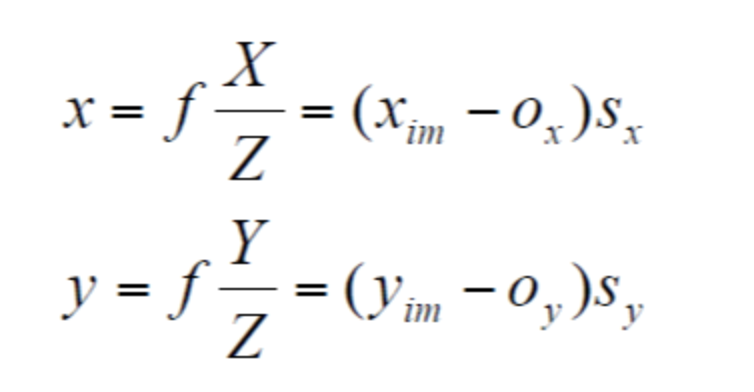
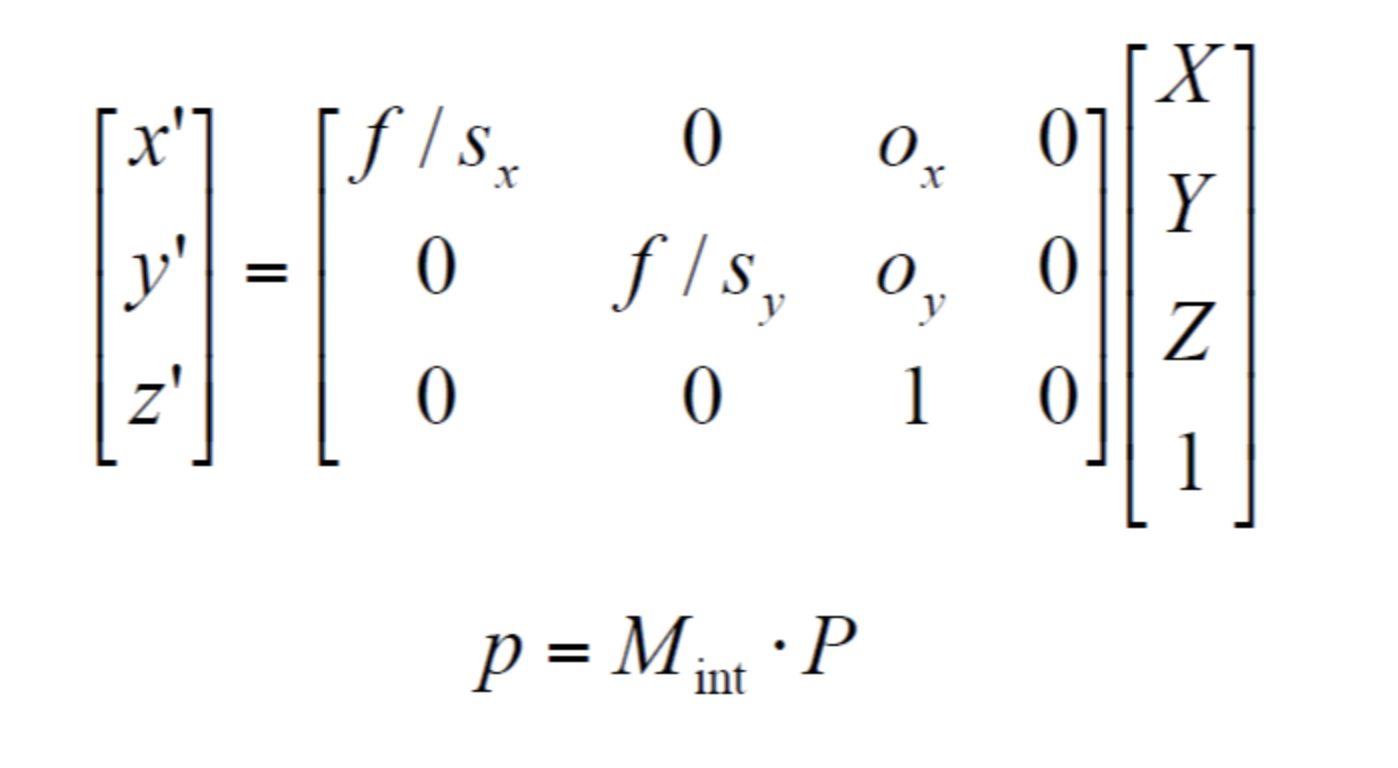
Effective Sizes : Sx and Sy
Ox ,Oy는 이미지의 중심의 원점을 뜻하며, Sx,Sy는 픽셀의 가로, 세로 비율을 뜻한다. 이를 Affine하는 연산을 한다.
이전의 Projection과 방금 Affine을 한 변환을 합치면 위와 같은 식으로 합칠 수 있다. Mint는 inter즉 카메라 내부에서 일어나는 변환(카메라가 이해한 좌표계->픽셀 좌표계)을 뜻한다. 이미 X, Z는 알고 f는 카메라가 조정할 수 있기에 x값을 알 수 있다
디지털 카메라의 이미지 센서는 CCD elements라고 불리는 광감지 소자들의 그리드로 구성된다. 센서의 CCD 엘리먼트(또는 포토다이오드)와 최종 디지털 이미지의 픽셀 사이에는 1:1 대응 관계가 존재한다. 즉, 센서의 각 CCD 엘리먼트는 촬영된 이미지의 단일 픽셀에 일적으로 대응된다.
CCD elements: 이미지 센서를 구성하는 소자의 개수
Aspect ratio: 이미지의 가로 세로 비율
2. Spaces Transformation
Spaces
1. 객체 공간 (Object Space, Model Space): 개별 객체의 관점에서 정의된 좌표 시스템으로 X, Y, Z 축은 객체 자체와 함께 회전한다. 즉, 객체를 돌리면 객체 공간의 축도 함께 회전하는 것과 같다. 또한 모델 공간이라고도 불린다.
2. 세계 공간 (World Space): 이 공간은 전체 3D 세계 (또는 가상 세계)를 정의하는 좌표 시스템으로 여러 개의 객체, 캐릭터, 카메라 등이 존재하며 모든 객체들은 세계 공간 내에 위치하며 서로 상대적인
위치 관계를 갖게 된다.
3. 카메라 공간 (Camera Space, Eye Space): 카메라의 관점에서 정의된 좌표 시스템으로 세계 공간에 있는 모든 점들의 위치는 카메라를 기준으로 재계산된다. EYE는 월드 공간에서의 카메라 위치, AT은 월드 공간에서 카메라가 바라보는 기준점, UP은 카메라의 상단이 가리키는 방향을 대략적으로 묘사하는 벡터이다. 이들 파라미터를 이용해 카메라 공간(camera space)이 정의되는 데, 그 원점은 EYE에 놓여진다. 카메라 공간의 기저를 {u, v, n}으로 표기하자. 가운데 상자는 EYE, AT, UP을 사용해 어떻게 {u, v, n}이 계산되는지 보여준다. 우리는 카메라 공간을 {u, v, n, EYE}로 표기한다.


4. 클립 공간 (Clip Space): 월드 공간에서 정의된 EYE, AT, UP을 카메라의 '외부'파라미터라고 본다면, 이제 카메라의 렌즈를 선택하고 줌인/줌아웃을 조절하는 것에 해당하는 '내부'파라미터를 정의해야한다. 일반적으로 카메라의 시야(Field of view; fov)는 제한되어 있기 때문에 카메라 공간의 모든 물체를 스크린에 담아낼 수 없다. 카메라의 가시 영역을 뷰 볼륨(veiw voilume)이라 부르는데, 이는 fovy, aspect, n, f 네 가지 파라미터를 사용해 결정된다.
fovy : field of view y-axis (y축 기준의 시야각)
aspect : 뷰 볼륨의 종횡비(가로세로 비율 = width/height)
fovy와 aspect에 의해 정의된 뷰 볼륨은 꼭지점을 원점에 두고 -z축을 중심축으로 가진 무한한 크기의 피라미드가 된다. 뷰 볼륨을 정의하는 나머지 파라미터 n과 f는 각각 원점으로부터 전방 평면(near plane)과 후방 평면(far plane)까지의 거리를 나타낸다. fovy와 aspect에 의해 정의된 무한한 크기의 뷰 볼륨은 z축에 수직인 전방 평면 z = -n과 후방 평면 z= -f에 의해 절단되어 유한한 크기의 뷰 볼륨으로 바뀐다. fovy와 aspect에 의해 정의된 무한한 크기의 뷰 볼륨은 z축에 수직인 전방 평면 z = -n과 후방 평면 z= -f에 의해 절단되어 유한한 크기의 뷰 볼륨으로 바뀐다.
Spaces Transformation
1. World Transform [Object Space to World Space]
월드 변환은 아핀 변환들로만 구성되었다면 [L | t]로 표기할 수 있다. L은 '누적된 선형 변환'을, t는 '누적된 이동'을 표현하는데, 노멀 변환에 있어 t는 무시해도 된다. 벡터는 이동에 의해 영향 받지 않기 때문에 생각을 안해도 된다.
노멀 변환, 정점과 노멀 모두 동일한 행렬 L에 의해 변환되었다
정점은 L에 의해 변환되지만, 노멀은 L^T에 의해 변환되어야한다.
위 그림에서 L을 노멀에 적용했을 때 문제가 발생했던 것은 L이 비균등 축소확대였기 때문이다. 만약 L이 비균등 축소확대를 포함하지 않는다면, 즉 L이 회전, 이동, 균등 축소 확대 중 하나이거나 이들이 결합된 경우라면, 노멀에 L을 적용해도 된다. 하지만, 알고리즘을 단순화하기 위해, L이 비균등 축소확대를 포함하건 말건 노멀 변환에는 무조건 L^-T를 사용할 것이다. 굳이 조건을 하나 더 달아 노멀에 L을 적용하지 말고 모든 경우에 L^-T를 사용하는 게 좋기 때문이다. 이해를 돕기 위하여 위 그림에서는 삼각형 노멀을 사용했지만, 폴리곤 메시 렌더링에 실제로 사용되는 것은 정점 노멀이다. 월드 공간 정점 노멀 계산에도 L^-T가 그대로 쓰인다.
2. View Transform [World Space to Camera Space]
세계 공간 좌표를 카메라 공간 좌표로 변환한다. 이는 직관적으로 카메라 공간 (u, v, n, EYE) 를 세계 공간 (e1, e2, e3, O) 에 중첩하는 과정으로 설명할 수 있다.

카메라 좌표계를 월드 좌표계에 포개 놓기 위함
하나의 공간에서 정의된 물체를 다른 공간으로 옮기는 것을 일반적으로 공간 이전(space change)이라고 부르는데, 월드 공간에서 카메라 공간으로의 이전은 카메라 좌표계 {u, v, n, EYE}를 월드 좌표계 {e1, e2, e3, O}에 포개 놓는 과정으로 묘사될 수 있다. 이를 위해서는 EYE를 먼저 O로 '이동'시킨 뒤 {u, v, n}을 {e1, e2, e3}와 일치하도록 '회전'시키면 된다. 이 과정에서 모든 물체는 카메라 좌표계를 따라 같이 움직인다.

'이동'과 '회전'이 필요하고, 이 두 변환이 결합된 것이 뷰 변환인데, 이는 월드 공간의 물체를 카메라 공간으로 옮긴다.
월드 공간 좌표가 (10, 2, 0)이던 주둥이 끝 정점도 이동과 회전을 거쳐 (0, 0, -10)의 좌표를 가지게 되었는데, 이제 월드 공간과 카메라 공간이 동일해졌으므로, 이 월드 공간의 좌표 (0, 0, -10)을 그대로 카메라 공간 좌표로 취하면 된다. 월드 공간에서 카메라 공간으로의 이전을 뷰 변환(view transform)혹은 카메라 변환(camera transform)이라 부른다.


회전 변환
이동에 의하여 월드 공간과 카메라 공간은 원점을 공유하게 된다. 따라서, 기저{u, v, n}은 회전을 통하여 {e1, e2, e3}에 포개질 수 있다. 이 회전은 카메라 공간의 기저 {u, v, n}을 행으로 가지는 행렬로 정의된다. 결국 물체들은 R에 의해 회전되어 공간 이전이 완료된다. 공간 이전을 구성하는 이러한 회전은 기저 이전(basis change)이라고 부른다.
3. Projection Transform (Camera Space to Clip Space)
투영 변환(projection transform)은 한 마디로 말하자면, 피라미드 모양의 뷰 프러스텀을 좌표계의 주축에 나란한 2x2x2 크기의 정육면체 뷰 볼륨으로 변형하는 것이다. 카메라 공간 물체는 이렇게 투영 변환을 거친 뒤, 2x2x2 크기의 정육면체에 대해 클리핑된다. 이런 점에서, 투영 변환 이후에 물체가 놓이는 공간을 클립 공간(clip space)이라고 따로 부른다.
뷰 프러스텀은 원점에 위치한 카메라로 수렴하는 투영선(projection lines)들의 집합으로 이해할 수 있다. 3차원 공간에서는 l1이 l2보다 길지만 투영 평면에서 이들은 동일한 길이를 가지게 된다. 즉 멀리 있는 물체가 작게 보이게 되는데 이것이 바로 원근법이다. 투영 변환의 결과, 모든 투영선들은 서로 평행해져 z축에 나란해졌다. 즉, 단일한 투영 방향을 가지게 되었다. 투영 변환은 Vertex Shader가 수행하는 마지막 연산이다. 투영 변환된 물체는 이제 하드웨어로 고정된 래스터라이저로 들어갈 것이다.
투영 행렬
3. Viewings
COP (Center of Projection) : 점 한 곳에 모이는 방식
DOP (Direction of Projection) : 평행하게 점이 아니라 일자로 빛이 퍼지는 방식
Orthographic Projections
모든 투사선이 서로 평행하게 유지되기 때문에, 실제 크기와 비율이 보존된다.
평행성: 모든 투사선이 서로 평행하게 유지된다.
크기 보존: 객체의 실제 크기와 비율이 보존된다.
왜곡 없음: 객체의 모양이 왜곡되지 않는다.
명확성: 객체의 윤곽선이 명확하게 표현된다.
정사 투영은 기술 도면, 지도 제작, 그래픽 디자인 등에 주로 사용된다.
Axonometric Projections
축성 투영은 정사 투영과 유사하게 평행선 투영을 사용하지만, 투사 방향을 특정 각도로 기울여 투영하기 때문에 객체의 깊이감을 표현할 수 있다.
명확성: 객체의 윤곽선과 각 부분의 관계를 명확하게 표현한다.
깊이감: 투사 방향을 기울여 투영함으로써 객체의 깊이감을 표현한다.
크기 비율 보존: 특정 축을 따라 객체의 크기 비율을 보존한다.
간단성: 비교적 간단한 방식으로 3D 객체를 2D 평면에 표현할 수 있다.
Axonometric Projections
정측 투영 (isometric projection): 세 주요 축이 서로 직각을 이루고 같은 비율로 축소되는 방식이다. 각 3개가 모두 같은 것이다.
이등측 투영 (dimetric projection): 한 쌍의 주요 축이 서로 직각을 이루고 같은 비율로 축소되고, 다른 한 축은 다른 비율로 축소되는 방식으로 각 2개만 같다.
삼측 투영 (trimetric projection): 세 주요 축 모두 서로 다른 비율로 축소되는 방식으로 각 3개가 모두 다르다
Oblique Projections
투영 방향과 투영면이 직각방향이 아니고 일정한 다른 각도를 이루고 있는 투영방법이다. 투영면의 최종 결과를 시점에서부터 바라보는 방향과 투영이 되는 투영선의 방향이 다른 각도를 이루고 있다. 투영선의 각도가 45도, 60도인 경우가 많이 사용되고 잇으며 직각 투영과 마찬가지로 객체들의 상대적인 크기가 유지된다. 투상선이 투상면에 대하여 45도의 경사를 가지는 카발리에(Cavalier)와 투상선이 투상면에 대해서 60도인 경사를 가지는 캐비닛(Cabinet)이 있다.
원근 투영( Perspective Projection )
시점에서 멀리 떨어져 있는 객체는 작게 투영되고 가까이 있는 객체는 상대적으로 크게 투영이 되어 사람의 눈으로 3차원 사물을 보듯이 보다 현실감 있는 투영 결과를 얻을 수 있는 투영 방법이다. 평행 투영과 달리 투영선들이 평행을 이루지 않는다. 따라서 투영면에 직각 방향으로 투영이 되지 않는다. 평행 투영에서는 투영 방향만 설정하면 되지만 원근 투영에서는 하나의 시점에서 3차원 객체를 바라본 모습이 3차원 투영면에 나타나므로 모튼 투영선이 시점에 모이게 된다.
원근 투영은 소실점( Vanish Point ) 수에 따라 1점 투영, 2점 투영, 3점 투영 등으로 나뉘며 이중 1점 투영은 게임에서 많이 이용하는데 1점 투영을 이용해야 물체의 3차원 깊이가 증가함에 따라 투영의 크기가 줄어드는 현상을 나타낼 수 있다.
소실점( Vanishing Point )
시각 평행선들이 무한이 멀리 있는 하나 또는 여러개의 점으로 모여지는 것을 말한다. 즉 물체의 연장선을 그었을 때 선과 선이 만나는 점을 소실점이라 한다.