
모델링은 모델링은 3D 공간에서 객체를 만드는 과정이다.
Polygon : 폴리곤은 폴리곤은 2D 공간 또는 3D 공간에서 선분으로 연결된 세 개 이상의 점으로 이루어진 폐곡선으로 3D 객체를 표현하는데 가장 기본적인 단위이다. 라인 루프로 닫혀진 오브젝트 이지만 내부를 가지고 있다. 폴리곤은 변의 수에 따라 n각형으로 분류되고 삼각형은 주로 게임 모델링, 사각형은 라이팅과 필름메이킹에 주로 이용된다.
Polygonal Mesh : Polygonal mesh는 3차원 컴퓨터 그래픽에서 polygon의 모음으로 이루어진 객체를 표현하는 데이터 구조로 각 다면체는 3개 이상의 점으로 구성되며, 이 점들은 선으로 연결되어 표면을 형성한다.
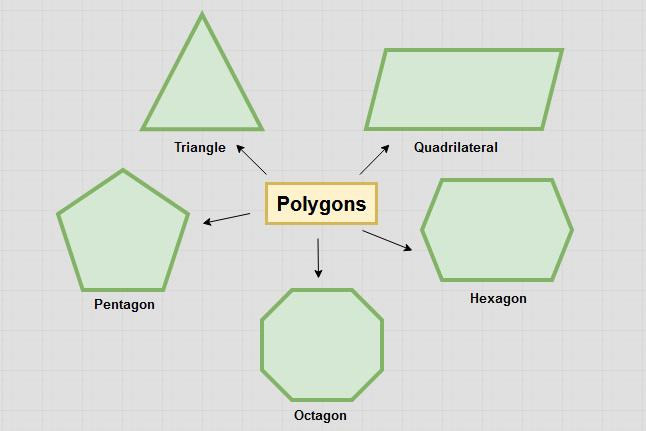

(좌) Polygon의 종류와 (우) Triangle polygon으로 형성된 Mesh
Polygonal Mesh Representation
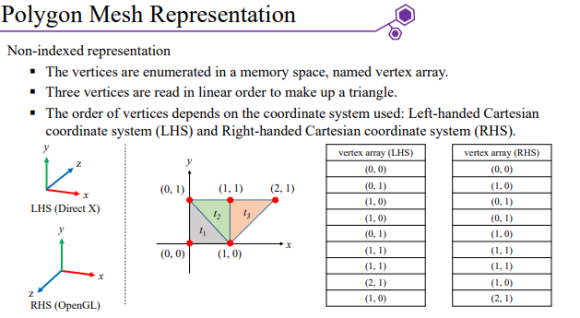
LHS and RHS
Non - indexed representation : 모든 꼭지점 정보와 삼각형 정보를 명시적으로 저장하여 메쉬를 구성
- Left-handed Cartesian coordinate system (LHS) : DirectX에서 이용되며 왼손으로 바깥쪽을 감아주며 정점을 배열에 저장
- Right-handed Cartesian coordinate system (RHS) : OpenGL에서 이용되며 오른손으로 바깥쪽을 감아주며 정점을 배열에 저장
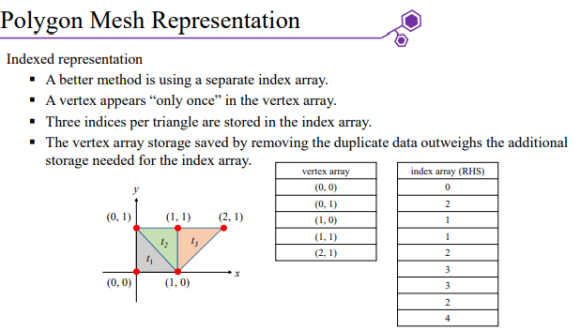
Indexed representation
Indexed representation : 비인덱스 방식은 꼭지점 데이터가 중복되어 저장되어 비효율적일 수 있다는 단점이 있는데, 꼭지점 데이터를 한 번만 저장하고 삼각형을 구성하는 꼭지점을 참조하는 인덱스만 별도로 저장하여 전체 메모리 사용량을 줄인다.
Mesh
닫힌 메쉬에서의 오일러 다면체 공식(v - e + f = 2), 삼각형 폴리곤의 특징, 면의 수 계산 공식을 이용하면 정점 수와 면 수의 관계는 f = 2v - 4 로 닫힌 삼각형 메쉬에서의 면의 수는 정점 수의 약 두 배이다. 메쉬가 커질 수록 면의 수는 정점 수의 약 두배에 가까워진다.
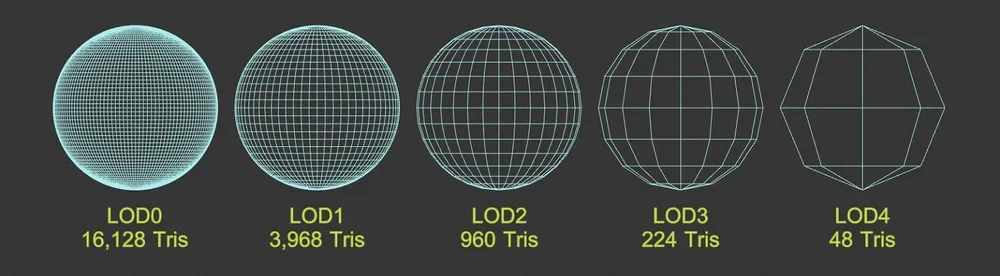
Level of Detail
레벨 오브 디테일(LOD) : 폴리곤의 Vertex 수는 해상도 혹은 LOD라고 하는데, 해상도가 증가함에 따라 메쉬의 모양은 원래 매끄러운 표면에 더 가까워지지만 메시를 처리하는데 필요한 시간도 증가한다.
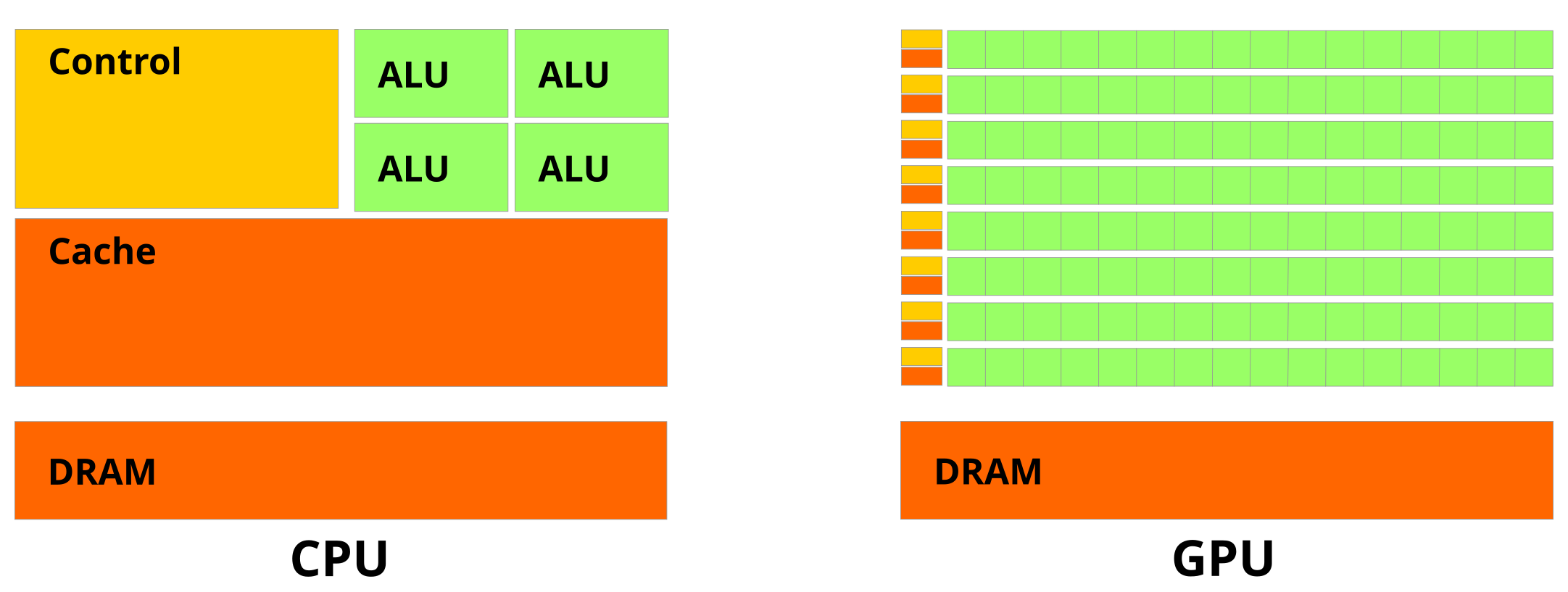
GPU vs CPU
GPU(Grapchics processing unit) : 컴퓨터의 그래픽을 처리하는 데 사용되는 하드웨어로 CPU보다 훨씬 더 많은 코어를 가지고 있어 그래픽을 더 빠르게 처리할 수 있다. 렌더링 작업을 전문적으로 수행하며 병렬 구조를 가지고 설계되어 많은 작업을 동시에 처리할 수 있는 구조 덕분에 빠르고 효과적인 렌더링이 가능하다. GPU는 운영체제를 혼자 실행할 수 없고 렌더링을 위해 필요한 데이터는 CPU쪽에서 데이터 버스를 통해 GPU 쪽으로 전송되어야 한다. CPU는 시스템 전체적인 작업을 처리하고 GPU는 그래픽 처리와 같은 특수 작업을 수행한다.
Implicit vs Explicit
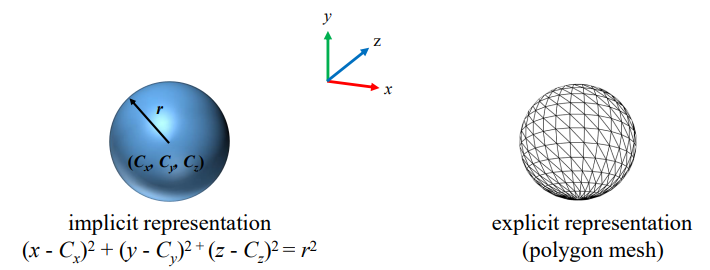
implicit and explicit representation in Polygon mesh
폴리곤 메쉬(Polygon Mesh) : 폴리곤으로 이루어진 3D 객체의 표면을 나타내는 구조로, 폴리곤 메쉬를 구성하는 모든 정점, 변, 면 정보를 직접적으로 저장하는 방식인 explicit representation과 직접적으로 저장하지 않고, 3D 공간에서 폴리곤 메쉬의 표면을 정의하는 수학적 방정식을 사용하는 방식을사용하는 implicit representation 방법이 있다. 컴퓨터 그래픽스에서는 polygon mesh를 사용하는데, 그 이유는 GPU가 polygon mesh를 사용하는데 최적화되어있기 때문이다.
모델의 움직임을 가정하면 다이나믹하게 토폴로지가 변화는 상황이 필요한데, 충돌이 발생하는 지의 여부를 확인하는 것이 복잡하다. 이러한 상황에 Implicit 방식이 유용하다. 함수를 이용해 표현하기 때문에 유기적인 형태나 물과 같이 복잡한 표면을 다루기에 좋다
Marching Cubes
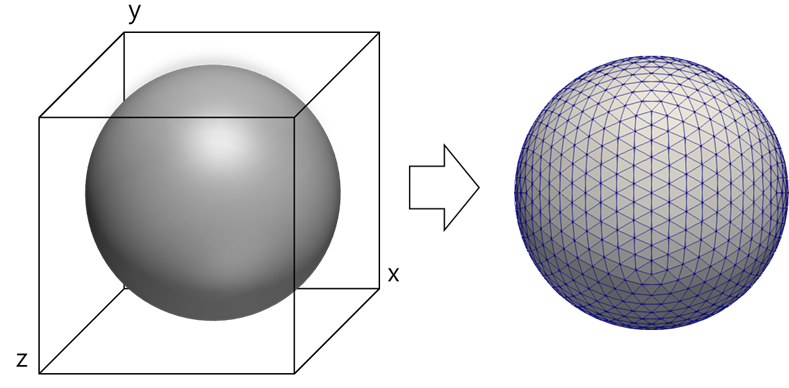
Marching Cubes
Marching Cube는 3차원 공간 내 각 점에 대한 밀도 값들로 3D mesh를 생성하는 알고리즘 중 하나이다. Surface냐 아니냐를 물어봐서 명시적으로 3D 모델을 만들어서 렌더링하는 것으로 implicit으로 부터 스캐닝해서 explicit으로 끌어내는 방법이다. 즉 implicit Surface를 삼각형으로 변환하여 3D 그리드로 implicit surface를 정의한다.
초록색 object를 mesh형태로 만들고자 한다. 3D 공간은 작은 단위의 투명색 cube로 표현 할 수 있고 아래 예시는 16x16x16의 cube grid로 구성되어 있다.

각 투명 cube는 총 8개의 vertex로 구성되어 있으며, 이 vertex들이 object에 포함되어 있는지 유무에 따라 미리 정의해 둔 polygon으로 변형하여, 전체 3D Mesh를 형성한다. 좀 더 구체적으로 설명하면, 투명 cube는 vertex가 object에 포함되는지 유무에 따라 총 2^8개(=256개)의 경우의 수로 나눌 수 있고 각 cube의 경우의 수 마다 surface polygon을 어떻게 배치 할지 사전에 구성해 둘 수 있다. 아래는 좌하단전면 1개 vertex를 기준점으로 15개의 경우의 수를 보여주며 다른 7개의 기준점으로 대칭/반전이동이 된다.

각 다격형의 시작점은 edge의 중간을 꼭지점으로 갖기 때문에, 모든 투명cube를 이어붙이면 3D Mesh를 만들 수 있다. 포인터 8개를 넣어서 아웃풋 값을 가진 뒤 결과를 같다 붙히면 marching cube 지나간 자리에 surface들이 생긴다.
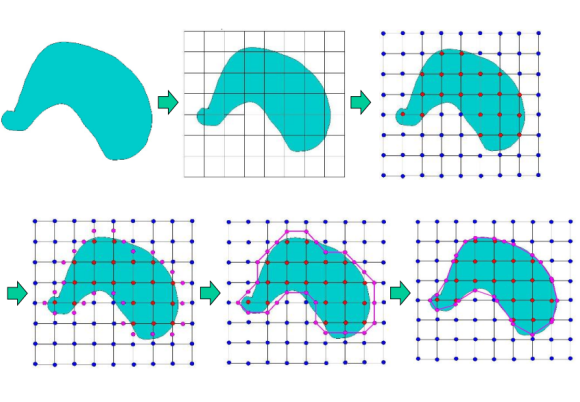
주의할 점은, 그리드 내에 점을 얻은 단계에서 끝나는게아니다. surface 안에있는 포인트와 밖 포인트 사이를 지나가니 surface를 찾고 안과 밖 페어의 점을 찾아서 중앙값을 찍는다. 그 후 점들 사이에서 어디에 더 해당하는지 찾고 더 자세하게는 서브디비전을 하면 된다. 이 때 -1 0 1 값이 있으면 절대값로 binary search 없이 찾을 수 있다.
Normals
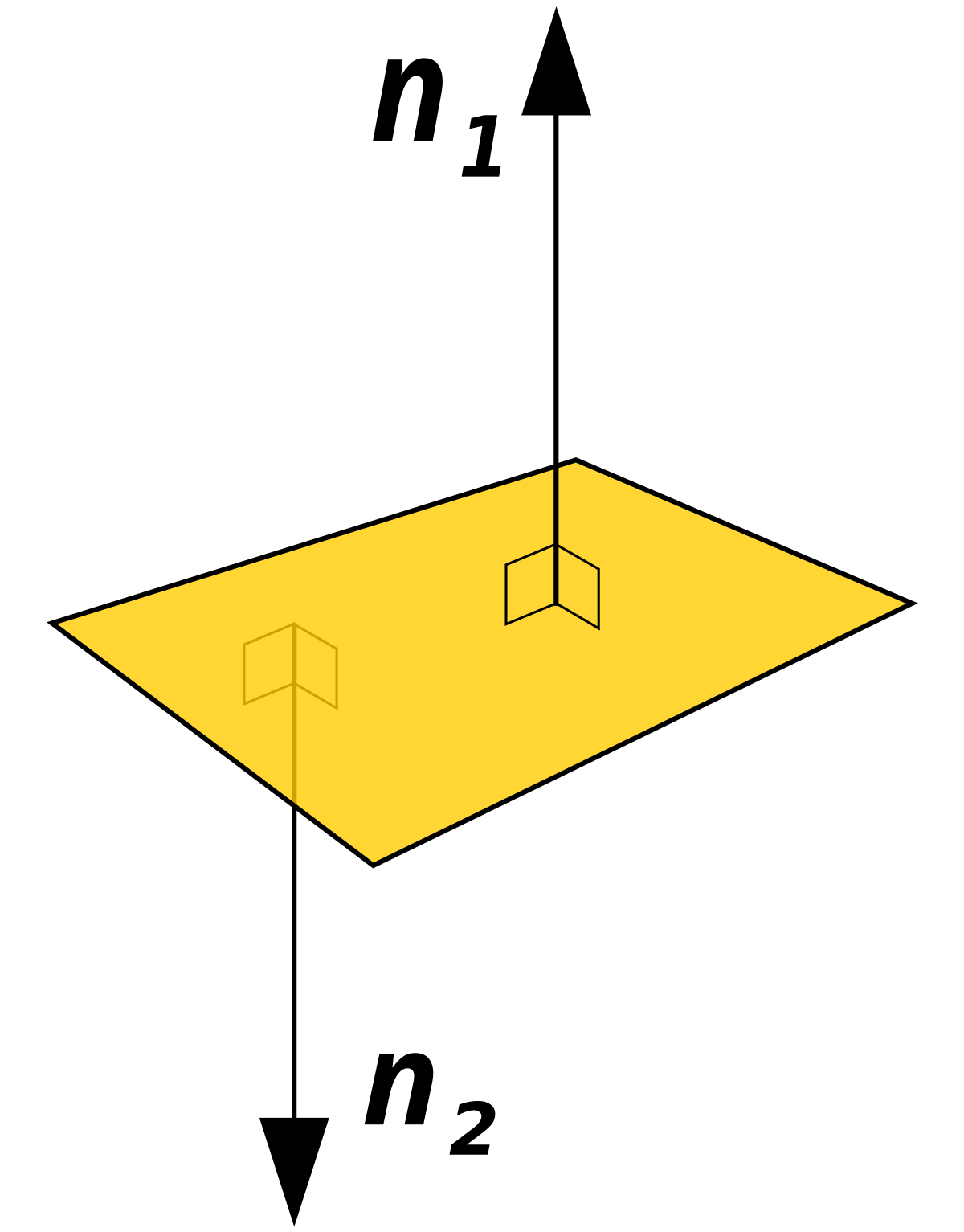
법선 벡터 (Normals) : 표면에 수직인 벡터로 표면 대신 꼭지점, 삼각형 등 다른 요소에도 법선 벡터를 정의할 수 있다. 법선 벡터는 주로 조명 및 음영, 충돌 감지, 뒷면 제거, 표면 질감 표현 등에 사영 된다.
세개의 점(Vertex)은 하나의 면(Face)을 만들고 이 면에 수직방향이 바로 Normal 방향인데, 세개의 점은 각각 정 반대방향으로 두개의 면을 만들 수 있기 때문에 이러한 노말방향이 없으면 모든 면을 양쪽으로 랜더링 걸어야 한다. 하지만 노말뱡향만 랜더링 걸게 되면 그 절반의 시간만 들이면 되는 것이다.
Surface Normals
Surface Normal
표면 법선 벡터 (Surface Normals) : 특정 지점에서 표면의 접선 평면에 수직 인 벡터로 물체 표면의 특정 지점에서의 밝기는 해당 지점의 법선 벡터와 광원 방향 사이의 각도 에 따라 결정된다.
노말값은 앞에서 살펴보았든 면의 앞뒷면을 살펴보는 정도로도 사용되지만. 하나의 기울기 값이라는 것 역시 노말값이 가진 속성이다. 아무런 매트리얼값도 들어가지 않은 기본 오브젝트에 하나의 라이팅이 떨어졌다고 가정하고, 이때 오브젝트의 각각 면은 빛의 방향과의 기울기 값의 차이로 인해 어두워 지거나 밝게 랜더링 되며 이에 따라 오브젝트는 하나의 물체로서 랜더링 되는 것이다. 여기서 바로 노말값이 사용된다. 노말방향은 다시 말해 각 면의 기울기 값을 대표하며, 노말방향과 라이팅이 서로 마주보고 있다면 이 부분이 가장 밝은 부분이 된다. 반대로 노말방향과 라이팅이 90도 이상 차이나게 되면 전혀 빛을 받지 못하게 되는 것이다.
Triangle Normal
Surface Normal
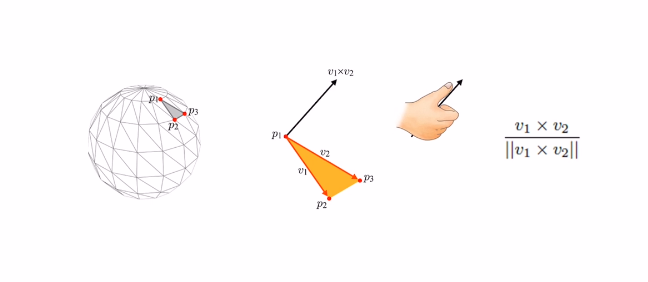
삼각형 법선 벡터 (Triangle Normal): 삼각형 메쉬는 꼭짓점(Vertex)과 연결 관계(Connectivity)로 정의되며, 매끄러운 표면을 만들기 위해서는 각 삼각형의 법선 벡터(Normal Vector)가 중요하다.
3D 도형에서 삼각형의 법선 벡터(normal vector)는 삼각형의 평면에 수직인 방향 벡터이다. 삼각형의 윤곽선을 따라 반시계 방향 (CCW)으로 정의된 세 점 (p1, p2, p3)이 있을 때, 다음과 같이 두 벡터의 외적(cross product)을 계산하여 법선 벡터를 구할 수 있다. vertex의 순서에 따라 방향이 바뀌는데 컴퓨터 그래픽스에서는 이 Normal Vector의 방향이 object의 바깥쪽을 향하는 것이 원칙으로 되어있다.
노말방향은 한 면에 하나 뿐이며. 그 면은 모두 같은 밝기로 랜더링 되어야 하기 때문에 각지고 끊어진 모습이 나온다. 이후에 같은 오브젝트라고 하더라도 부드럽게 처리하는 랜더링 기술이 쓰였는데. Soft Edge라는 개념이다. 그리고. 이 Vertex부분이 랜더링의 중심값이 되며 이로 부터 다음 버텍스까지는 중간값으로 처리하게 되는 것이다.
Vertex Normal

Vertex Normal
꼭지점 법선 벡터 (Vertex Normal): 꼭지점을 기준으로 주변 삼각형들의 법선 벡터 평균이다. 꼭짓점 법선 벡터는 각 꼭짓점에 연결된 벡터로, 매끄러운 표면의 기울기를 근사하여 표현하는데, 렌더링 프로그램은 이 꼭짓점 법선 벡터를 이용하여 물체의 명암 처리를 계산한다.
- 평균 계산: 꼭짓점과 연결된 모든 삼각형들의 법선 벡터를 평균하여 꼭짓점 법선 벡터를 계산한다.
- GPU 전송: 계산된 꼭짓점 법선 벡터 데이터는 보통 꼭짓점 배열(Vertex Array)을 통해 그래픽 처리 장치(GPU)로 전송되며 GPU는 이 데이터를 이용하여 각 픽셀의 색상을 결정한다.
Surface vs Triangle vs Vertex normals

Smooth Shading
Flat Shading: Triangel Normal이 가장 중요. 삼각형 법선은 전체 삼각형에 걸쳐 조명을 위한 단일 방향을 정의하고 삼각형을 이루는 세 점 모두 같은 법선 값을 사용하여 조명 효과가 계산된다
Smooth Shading: 매끄러운 음영 처리에서는 Vertex Normal이 중요하다. 꼭짓점 법선은 인접한 꼭짓점의 법선 값을 보간하여 구부러진 표면을 시뮬레이션 할 수 있게 해준다. 즉, 각 꼭짓점마다 계산된 법선 값을 이용하여 삼각형 안쪽의 점에 대한 법선을 부드럽게 변화시켜 사실적인 효과를 만들어낸다
physics calculations : 충돌 감지, 정확한 반사/굴절 효과와 같은 물리 계산이나 그래픽 효과를 위해서는 특정 지점에서의 실제 표면 법선 값이 필요하다. 꼭짓점 법선과 삼각형 법선은 근사치이기 때문에 이러한 경우에는 표면 위 특정 위치에 대한 정확한 법선 계산이 필요하다
Export vs Import

Polygon mesh to run-time 3D application : 오프라인 그래픽 패키지 를 사용하여 만든 폴리곤 메쉬와 관련 데이터는 파일 형식으로 저장되며, 이를 런타임 3D 애플리케이션 프로그램으로 넘겨줄 수 있다
- Export : 데이터를 다른 애플리케이션에서 사용할 수 있는 형식으로 출력
- Import : 내보내진 데이터를 가져오는 작업
폴리곤 메쉬 데이터를 저장하는 파일 포맷은 다양하며 그 중에서 인기 있는 포맷 중 하나는 .obj 파일이다. 파일 내 저장된 데이터는 3D 애플리케이션의 꼭짓점 배열과 인덱스 배열로 가져온다. 메쉬가 48개의 삼각형으로 구성되어 있으므로 인덱스 배열은 144개 (48 × 3)의 요소를 갖게 된다.
'Computer Graphics > Graphics Theory' 카테고리의 다른 글
| Graphics Theory [2] : 변환 (1) | 2024.09.18 |
|---|---|
| Graphics Theory [0] : 컴퓨터 그래픽스란? (0) | 2024.09.18 |