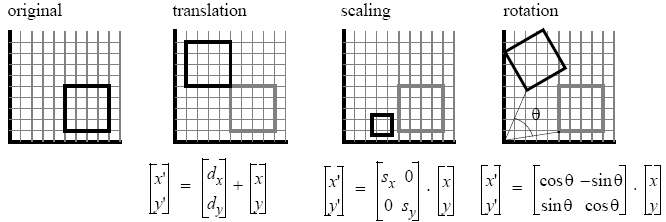
컴퓨터 그래픽스에서 변환(Transformation)은 3D 공간에서 객체의 위치, 방향, 크기를 조작하는 데 사용하는 수학적 연산으로 이동 변환, 회전 변환, 축소/확대 변환, 전단 변환, 투시 변환 등이 있다. 예를 들어, 게임 엔진에서는 이동 변환을 통해 캐릭터를 위치시킬 수 있고, 회전 변환으로 캐릭터의 방향을 조정하며, 축소/확대 변환으로 객체의 크기를 조절 할 수 있다. 구체적인 변환의 수학적인 행렬을 알아보기에 앞서 변환 그룹에 대한 이해를 해두는 것이 좋다,
Transformation Group

변환을 행렬로 간단하게 표현하기 위해선 잘 정리되어있는 성격이 필요한데, 변환 그룹의 세가지 성격을 서로 다른 변환들이 가지고 있다면 그 변환을 그룹으로 표현할 수 있다. 변환 그룹은 변환 간의 연산 규칙이 명확하고 모든 변환에 대해 역원이 존재하기 때문에 계산이 쉽고 예측 가능하다. 3D 공간에서 객체의 위치, 방향, 크기를 조작하는 변환의 집합으로 변환 그룹을 사용하면 여러 변환을 한 번에 적용할 수 있고 하나의 그룹으로 묶어 관리할 수 있으므로 중요한 역할을 한다.
닫힘: 그룹 내 두 변환을 연산하여도 그룹 내 변환이 된다.
항등원: 변환을 아무것도 하지 않는 항등원 변환이 존재한다.
역원: 그룹 내 모든 변환에 대해 역변환이 존재한다.
같은 그룹을 만족한다면 변환은 연산의 역원 (inverse) 존재가 보장되며 결합 법칙 (associative property)을 만족하기에 여러 변환을 연속적으로 적용할 때 순서에 상관없이 같은 결과를 얻을 수 있다.
Transformation Matrix
1. Scaling Transformation
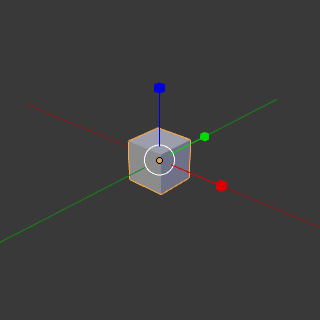
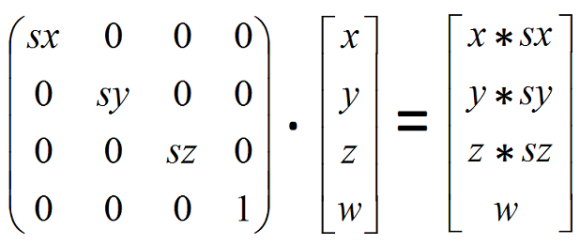
크기 변환 (Scaling) : 객체의 크기를 조절하는 과정으로 객체를 구성하는 각 꼭짓점의 좌표에 스칼라(Scalar)를 곱하는 방식으로 이루어진다. 선형대수에서 다룬 행렬-벡터의 선형 변환을 각 좌표마다 적용한다고 생각하면 된다. 부연 설명이 필요없는 가장 직관적으로 이해하기 쉬운 변환이다.
고정점: 확대 변환을 적용해도 변하지 않는 점으로 확대의 중심점이라고 생각하면 편리하다.
확대 방향: 확대가 이루어지는 방향을 나타낸다. 일반적으로 x축, y축에 대한 확대를 사용하며, 빗방향 확대도 가능하다.
확대 배율: 1보다 큰 값은 확대를, 1보다 작은 값은 축소를 의미한다.
모든 스케일링 요소가 동일한 값을 가지는 경우 uniform scaling이라고 하며 그렇지 않다면 non-uniform Scaling 이라고 한다.
2. Rotation Transformation
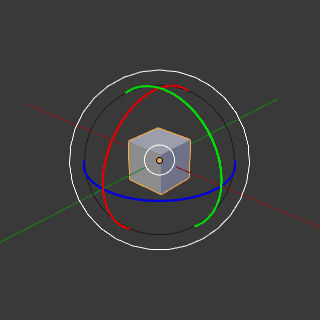

회전 변환 (Rotation) : 축을 기준으로 물체를 돌리는 과정이다. 회전은 물체가 이동하는 방향에 따라 시계 방향 회전(Clockwise rotation) 반시계 방향 회전(Counterclockwise rotation) 으로 나뉜다. 회전 변환에서는 삼각 함수가 중요한 역할을 한다. 위 이미지의 설명을 참고하자.
고정점 (fixed point): 회전 변환을 적용해도 변하지 않는 점으로 회전의 중심점이라고 생각하면 된다.
회전 각도 (rotation angle): 양의 값은 반시계 방향, 음의 값은 시계 방향 회전을 의미합니다.
3D 회전 축 (rotation axis in 3D): 회전이 발생하는 축을 나타낸다.
기본 회전 방향은 반시계 방향이지만 시계 방향으로 θ(시타) 만큼 회전하는 행렬은 반시계 방향 회전 행렬에 -θ(음의 시타) 를 넣어 계산할 수도 있다.
지금까지 배운 회전은 모두 원점을 중심으로 이루어지는 회전이었다. 임의의 점 (a, b) 을 중심으로 물체를 회전시키는 방법은 다음과 같다. 회전 중심이 원점이 아니므로, 회전시키고 싶은 점 (x, y) 를 (-a, -b)만큼 이동하고 이동된 점 p' 를 중심으로 원래 각도 (θ)만큼 회전한다. 그 후 회전을 마친 점 p'' 를 다시 (a, b)만큼 이동, 1번의 이동과 반대 방향으로 이동하여 원래 위치의 회전 중심으로 되돌린다.
하나의 점(point)을 중심으로 이루어지는 2차원 회전과 달리 3차원 회전은 축(Axis)을 중심으로 회전한다. x축을 중심으로 회전하는 경우, x 좌표 값은 변하지 않는다. 즉 x' = x이다. z축을 중심으로 회전하는 경우 오른손 규칙에 따라 손가락 말단은 x축에서 y축 방향으로 휘어진다. 축 간의 치환을 통해 다른 축을 중심으로 하는 회전 행렬을 도출할 수있다.
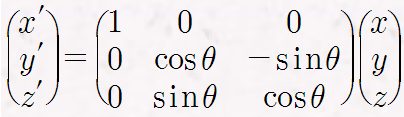
X축 기준 회전
Y축을 기준으로 회전하면, Y값은 변치 않고 X,Z값만 수정되며,
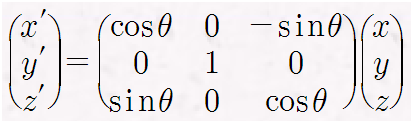
Y축 기준 회전
Z축을 기준으로 회전하면 Z값은 변치 않고 X,Y값만 수정된다.
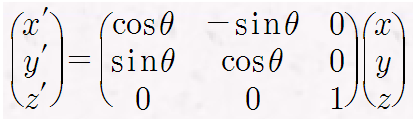
Z축 기준 회전
3. Translation Transformation
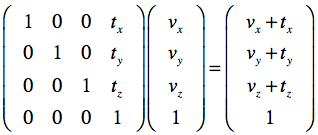
이동 변환(Translation) : 3D 공간에서 객체를 축 방향으로 이동시키는 과정이다. 크기 변환이나 회전 변환과 달리 평행 이동은 벡터 더하기로 나타낸다. 평행이동은 (x, y) 좌표를 (x + dx, y + dy) 좌표로 이동시키는 과정이고 (dx,dy)를 평행 이동 벡터라고 한다. 이를 선형 변환으로 표현하기 위해 2차원 좌표계에서 점의 위치를 (x,y) 좌표로 나타낸다면 이 점을 (x,y,1) 형태의 3차원 Homogeneous Coordinates를 이용해야한다.
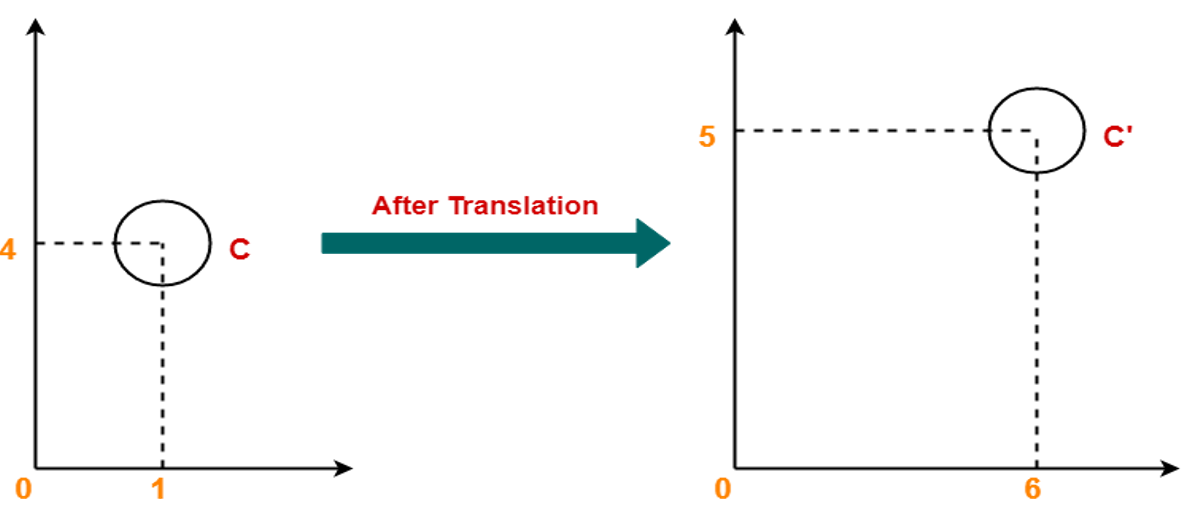
선형 대수 파트에서 보았듯이 선형 변환은 원점에 고정되어있다는 것을 전제로 하지만 이동 변환에 의해 새롭게 형성되는 벡터 공간은 원점에서 떨어지게 된다. 행렬식으로 이동 변환을 계산하는 것은 지금까지 진행한 곱셈 연산이 아닌 덧셈 연산을 수행하면 간단하게 해결할 수 있지만, 선형 변환을 사용해 이동 변환을 구하는 방법 중 하나는 차원을 늘리는 것이다.
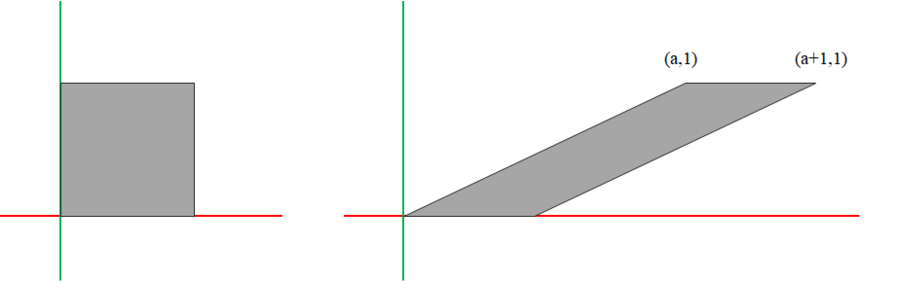
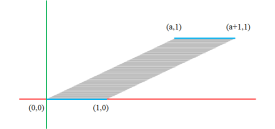
현재 공간보다 한 차원을 늘린 후에 밀기(Shear) 변환을 적용시켜 벡터 공간을 한쪽 방향으로 민 후, 밀린 새로운 공간에서 차원을 줄여 필요한 공간을 수집하면 선형 변환을 유지하면서 우리가 원하는 이동한 공간을 얻을 수 있게 된다.
즉 선형 변환은 2차원 공간에서 수행하고, 우리는 이의 결과물에서 1차원만 활용한다는 개념으로 접근하면, 선형성을 유지하면서 우리가 원하는 이동 변환을 구할 수 있는 것이다. 2차원 이동 변환도 같은 방식을 사용하면 선형 변환으로 구현이 가능하다. 벡터 공간을 1차수 높여 3차원으로 구성하고 이에 밀기 변환을 적용한 후 나온 벡터 공간에서 특정 z 값을 사용해 2차원만 빼내 활용하면 된다. 여기도 우리가 원하는 평면을 제공하는 z 값은 1이다.
4. 기타 변환 행렬(Euclidean, Similarity, Affine, Projective)

Euclidean(Rigid) : Rotation + Translation
Similarity : Rotation + Translation + Scale
Affine : Rotation + Translation + Scale + Aspect Ration + Skew
Projective : Rotation + Translation + Scale + Aspect Ration + Skew + Perspective Warp

Rotation 변환과 Transformation 변환이 결합된 Euclidean의 경우처럼 여러 변환이 결합된 변환 그룹의 행렬은 Partioned Matrices로 간략하게 표현할 수 있다.
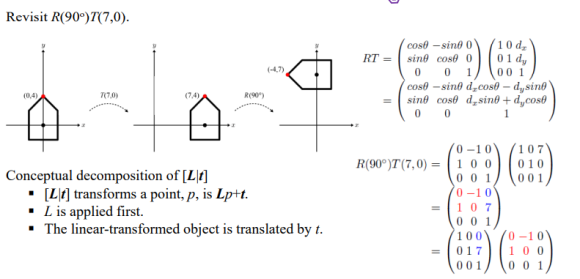
축소확대, 회전, 이동의 세 변환 중, 축소확대와 회전은 선형 변환 범주에 속하지만, 이동은 그렇지 않다. 선형변환과 이동을 포함하는 범주를 아핀 변환(affine transform)이라 한다. 2차원 아핀 변환은 3x3 행렬로 표현되므로, 몇 개의 아핀 변환이 주어지건 이는 모두 하나의 행렬로 결합 가능하다. 행렬의 3번 행은 항상 (0 0 1)로 고정되는데, 이렇게 고정불변인 3번 행을 무시하고 나머지 2x3 행렬을 [L | t]로 표기한다. L은 왼쪽의 2x2 행렬을, t는 3번열을 말한다. 여러 개의 아핀 변환이 결합된 [L | t]에서, L은 '누적된 선형 변환'을, t는 '누적된 이동'을 표현한다.
[L | t]로 변환하는 것을 개념적으로 해석하면, 그 물체에 L을 먼저 적용하고 그렇게 선형 변환된 물체에 t를 적용하는 것과 같다. 즉, 폴리곤 메시로 표현된 물체의 각 정점을 p라 할 때, Lp + t 방식으로 변환이 이뤄지는 것이다. 축소확대 없이 회전과 이동이 결합된 변환을 생각해보자. 이 변환은 물체의 방향과 위치를 변경시킬 뿐 그 물체의 외양에는 영향을 미치지 못한다. 이런 점에서 이를 강체 변환(rigid motion)이라고도 부른다.
Object-space Basis and Rotation
오브젝트 공간에서 한 물체의 모델링이 완료되면, 그 물체는 자신의 오브젝트 공간과 일체가 된다. 즉, 물체를 움직이게 되면 그 오브젝트 공간도 따라서 같이 움직인다.
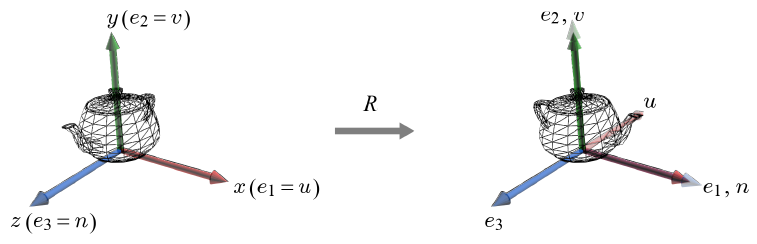
한 물체의 오브젝트 공간 기저는 그 물체의 방향을 표현한다.
오브젝트 공간에서 한 물체의 모델링이 완료되면, 그 물체는 자신의 오브젝트 공간과 일체가 된다. 즉, 물체를 움직이게 되면 그 오브젝트 공간도 따라서 같이 움직인다. (e1, e2, e3)는 월드 공간의 기저를, (u, v, n)은 오브젝트 공간의 기저를 나타낸다. 초기에 그 둘은 일치하지만, 물체가 회전하며, 오브젝트 공간 기저 (u, v, n)은 (e1, e2, e3)와 다르게 된다. 따라서 회전 후 물체의 방향은 (u, v, n)으로 표현할 수 있다.

예시에서 확인할 수 있듯, 회전된 물체의 오브젝트 공간 기저인 (u, v, n)이 주어졌다면, 그 회전 행렬을 즉각 정의할 수 있다. 즉, (u, v, n)으로 세 열을 채우면 된다.
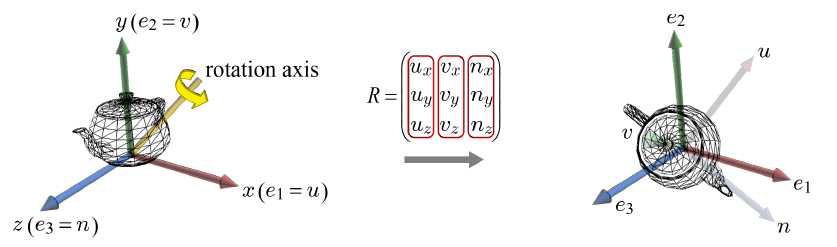
회전축이 주축일 뿐만 아니라 임의의 축일 때도 동일하게 적용된다. 임의의 축에서의 회전에 대한 자세한 내용은 아래 링크를 참고
5. Application
World Transform
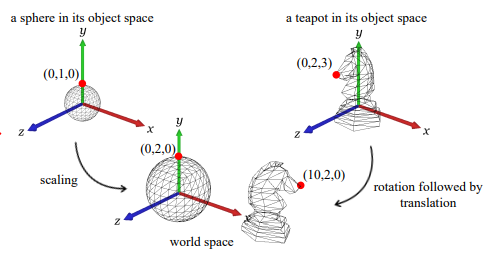
하나의 물체를 모델하는 데 사용된 좌표계를 오브젝트 공간(object space)이라 부른다. 각자의 오브젝트 공간에서 정의된 물체들로 3차원 가상 환경을 구성하려면 이들을 하나의 좌표계로 통합해야 하는데, 이 좌표계를 월드 공간(world space)이라 부른다. 그림과 같이 각각의 구와 주전자를 만들고 월드 변환(world transform)을 통해 월드 공간으로 옮겨진다. 이 과정에서 앞서 말한 아핀 변환의 모든 것이 적용된다. 2차원 아핀 변환의 특성은 3차원에서도 그대로 유지되며, 행렬 곱셈에서는 교환 법칙이 성립하지 않는다.
Inverse of Rotation
컴퓨터 그래픽스에서 역변환(inverse transfrom)은 자주 사용되는 개념이다.변위 벡터가 (dx, dy, dz)인 이동 T의 역변환은 (-dx, -dy, -dz_)만큼 이동하는 것이다.

T와 T의 역변환, T의 역행렬
회전의 역변환을 정의해 보자. 우리는 항상 오브젝트 공간 기저 (u, v, n)이 직교 정규 성질을 가진다고 가정한다. 따라서, 하나의 기저 벡터가 자신과 내적되었을 때 그 결과는 1이다. 반면, 서로 다른 기저 벡터 간 내적은 0이 된다. 따라서 회전의 전치행렬을 취하면 바로 역변환을 얻게 된다.
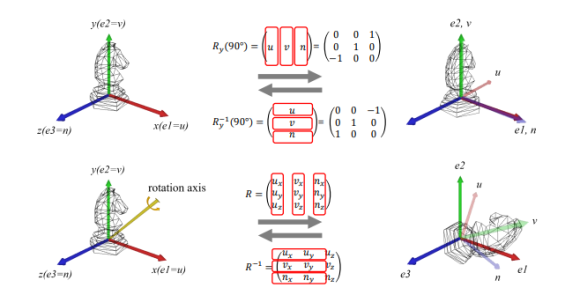
역회전
Right-hand System vs. Left-hand System
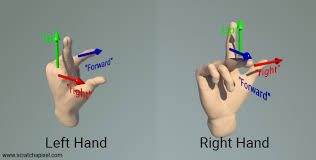
3D Cartesian coordinate
3차원 카테시안 좌표계는 Right-hand System 또는 Left-hand System 체계를 사용할 수 있다.
RHS : 오른손의 엄지가 양의 z 축 방향을 가리키고, 나머지 네 손가락은 x 축에서 y 축으로 구부러져 있을 때를 말한다. 이와 같은 손 모양을 만들면 마치 축들이 서로 수직이며, x 축이 양의 방향으로 오른쪽, y 축이 양의 방향으로 앞쪽, 그리고 z 축이 양의 방향으로 위쪽을 가리키는 것을 직관적으로 이해할 수 있다.
LHS : 왼손의 엄지가 양의 z 축 방향을 가리키고, 나머지 네 손가락은 x 축에서 y 축으로 구부러져 있을 때를 말한다. 우 계열과는 반대 방향으로 손가락을 구부려야 한다.
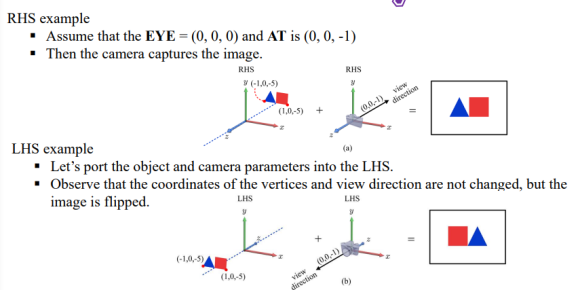
RHS example
카메라 위치 (EYE): (0, 0, 0)
응시점 (AT): (0, 0, -1)
꼭짓점 좌표와 시야 방향 자체는 변경되지 않는다. 하지만 최종 이미지는 반전된다.
우 손 ⇔ 좌 손 변환
앞에서 본 반전된 이미지를 피하기 위해서는 객체와 시야 관련 파라미터의 z 좌표값을 모두 반전시켜야 하며 이 z 좌표 반전은 개념적으로 z 축의 반전과 동일하다.
우 손 좌표계: EYE = (0, 0, 0) AT = (0, 0, -1)
좌 손 좌표계 (z 좌표 반전 적용): EYE = (0, 0, 0) AT = (0, 0, 1) <- z 값이 반전됨
위와 같이 z 값을 반전시킴으로써 우 손 좌표계와 좌 손 좌표계 간의 변환을 수행할 수 있다.
DirectX: 기본 좌표계에서 z 축이 앞쪽 방향을 나타낸다.
OpenGL: 기본 좌표계에서 z 축이 뒤쪽 방향을 나타낸다.
'Computer Graphics > Graphics Theory' 카테고리의 다른 글
| Computer Graphics [5] : 카메라 시점 (Camera View) (0) | 2025.02.02 |
|---|---|
| Computer Graphics [4]: 셰이더 (Shader) (1) | 2025.01.11 |
| Computer Graphics [3]: 텍스쳐 (Texture) (1) | 2025.01.11 |
| Graphics Theory [7] : 렌더링 파이프라인 (Rendering Pipeline) (1) | 2024.10.08 |
| Computer Graphics [1] : 모델링 (Modeling) (1) | 2024.09.18 |