
셰이더 (Shader)는 컴퓨터 그래픽스에서 빛과 물체의 상호작용을 수학적으로 계산하여 화면에 보이는 최종 이미지를 결정하는 단계이다. 기본적으로 셰이더는 3D 장면의 기하학적 정보와 물리적 속성을 바탕으로 색상, 밝기, 질감 등을 연산하여 현실감 있는 시각적 표현을 만들어낸다. 이는 인간이 실제 세계를 인식하는 과정과 유사한 원리를 따르며, 빛의 반사, 산란, 투과 같은 광학적 현상을 수식으로 모델링하여 그래픽 요소에 적용한다. 따라서 셰이더는 단순히 화면을 그리는 도구가 아니라, 가상의 세계를 더욱 사실적으로 시뮬레이션하는 중요한 개념으로 이해할 수 있다.
1. Lighting
셰이더에서 빛을 이해하는 것은 화면에 표현되는 물체의 색상, 질감, 입체감, 그리고 현실감을 결정하는 핵심 요소이다. 빛은 물체의 표면과 상호작용하면서 반사, 굴절, 산란 등의 효과를 만들어내며, 이를 수학적으로 정확하게 모델링해야 현실적인 그래픽을 구현할 수 있다. 예를 들어, 같은 색상의 물체라도 빛의 방향과 강도에 따라 완전히 다른 시각적 인상을 줄 수 있으며, 실시간 렌더링에서는 조명 조건에 따라 동적으로 변화하는 장면을 표현하는 것이 필수적이다. 따라서 셰이더에서 빛의 물리적 특성과 그 영향을 정확하게 계산하는 것은 사실적인 그래픽과 몰입감 있는 가상 환경을 만들기 위한 핵심 원리이다.
1.1 Basic Principles of Light
셰이더의 라이팅은 3D 가상 세계에서 빛이 물체와 상호작용하는 방식을 수학적으로 모델링하여 최종 이미지의 색상과 밝기를 결정하는 과정이다. 이 과정은 실제 세상에서 빛이 물체에 닿아 반사(Reflection), 흡수(Absorption), 산란(Scattering)되는 현상을 모방하는 것이다.
빛이 물체 표면에 도달하면 표면의 재질 특성에 따라 빛이 일부는 반사되고 일부는 흡수된다. 또한 산란 현상에 의해 빛이 여러 방향으로 흩어지는데, 산란된 빛 중 일부는 다시 다른 물체나 원래의 광원으로 돌아올 수 있다. 이러한 반복적인 과정을 다중 산란(Multiple Scattering)이라고 하며, 렌더링 방정식(Rendering Equation)의 근간을 이루는 것이다. 렌더링 방정식은 무한한 빛의 상호작용을 계산하여 각 픽셀에 도달하는 최종 빛의 양을 산출하는 원리이다. 표면이 부드러울수록 특정 방향으로 집중된 반사가, 거칠수록 다양한 방향으로 빛이 분산되는 효과를 보인다.
💡 Rendering Equation
렌더링 방정식(Rendering Equation)은 장면 내에서 빛의 상호작용을 수학적으로 모델링하는 식으로, 한 지점에서 특정 방향으로 나가는 빛의 양(방사도, Radiance)을 계산하는 기본 원리이다. 이 방정식은 다음과 같이 표현된다.
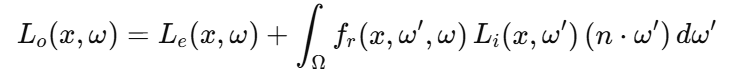
여기서 각 항의 의미는 다음과 같다.
- Lo(x,ω) : 점 x에서 방향 ω로 나가는 최종 방사도이다. 이는 관찰자에게 도달하는 빛의 양을 나타낸다.
- Le(x,ω) : 점 x에서 방향 ω로 직접 방출되는 방사도이다. 예를 들어, 광원이나 발광 물체에서 직접 나오는 빛을 의미한다.
- Ω : 점 x에서 반사되어 들어오는 모든 가능한 방향의 집합이다.
- fr(x,ω′,ω): 점 에서 들어오는 방향 ω의 빛이 반사되어 나가는 방향 ω로 전달되는 BRDF(Bidirectional Reflectance Distribution Function)이다. 이는 물체의 재질에 따른 빛의 반사 특성을 결정한다.
- Li(x,ω′): 점 x에 들어오는 빛의 방사도이다.
- (n⋅ω′): 점 의 표면 법선 n과 들어오는 빛의 방향 ω 사이의 내적으로, 입사각에 따른 빛의 기여도를 조절하는 역할을 한다. 표면에 직각으로 들어오는 빛은 (n⋅ω′) 값이 크고, 표면에 비스듬히 들어오는 빛은 값이 작다.
- dω′ : 무한한 입사 방향에 대한 미소한 영역이다.
이 방정식은 두 부분으로 구성된다. 첫 번째 항인 Le(x,ω)는 물체 자체가 빛을 내뿜는 경우를 나타내며, 두 번째 항은 모든 입사 빛이 물체 표면에서 산란되어 나가는 기여도를 적분하여 계산한 것이다. 이 적분 항은 실제로 빛이 물체 표면에 부딪혀 반사되고 산란되며, 때로는 흡수되는 과정을 모두 포함하여, 복잡한 빛의 상호작용을 한 번에 표현한다.
렌더링 방정식은 이처럼 단순한 수식으로 다양한 빛의 물리적 현상을 모델링할 수 있기 때문에, 사실적인 이미지를 생성하는 데 중요한 역할을 한다. 다만, 이 방정식을 직접적으로 계산하는 것은 매우 복잡하여 주로 근사 기법(예를 들어, 몬테 카를로 적분법)을 사용하여 해결한다.

Local Shading은 개별 폴리곤 단위로 셰이딩을 계산하는 방식으로, 각 폴리곤과 빛원 간의 상호 작용만을 고려하여 표면의 색상을 결정하는 방식이다. 반면, Global Shading은 모든 물체와 광원을 포함하여 전체적인 빛의 이동 경로를 계산함으로써, 실제 세계와 유사한 조명 효과를 만들어내는 방식이다. 이 방식은 물체 간의 복잡한 반사광이나 부드러운 그림자 효과 등 정교한 조명 현상을 구현할 수 있다. 그러나 실시간 그래픽에서는 이미지가 완벽하게 정확하지 않더라도 사용자에게 사실적으로 보이는 것이 중요하다. 때문에 실시간 렌더링에서는 Global Shading의 완벽한 구현이 어려워 Phong Shading과 같은 다양한 근사 기법을 사용하여 글로벌 조명 효과를 모사한다.
💡 BRDF vs BTDF vs BSTF
1. 2. Lighting Model

Phong Reflection
조명 또는 음영 처리 과정은 광원의 성질, 물체의 표면 특성, 그리고 관찰자의 위치를 고려하여 빛이 어떻게 반사되고 확산되는지를 시뮬레이션한다. 여기에는 조명의 반사 특성을 계산하는 조명 모델이 필요한데, 주로 Phong 모델이 사용된다. 이 모델을 사용하는 이유는 물체의 표면이 빛을 받았을 때 보다 현실적인 반사 효과를 구현하고, 연산량이 비교적 적어 실시간 그래픽스에서도 효율적으로 적용할 수 있기 때문이다.
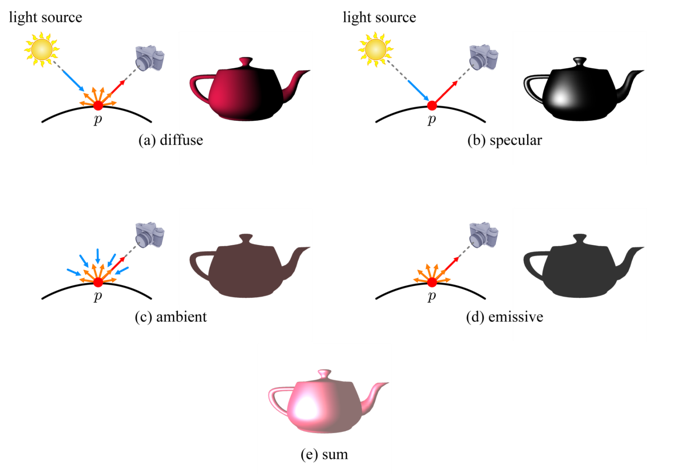
Phong Models
Phong 모델은 물체의 표면에서 반사되는 빛을 계산하기 위해 네 가지 요소를 합하여 정의된다. 이 모델에서 발산광 me는 물체가 자체적으로 빛을 내지 않는다면 제외할 수 있으며, 램버시안 표면과 유사한 물체는 난반사가 강하게 나타나므로 확산 반사 계수 md 를 크게, 정반사 계수 ms 를 작게 설정해야 한다. 반면, 표면이 매끄럽고 반짝이는 금속성 물체를 표현하기 위해서는 정반사 성분이 두드러지도록 ms 를 크게 설정하는 것이 적절하다. 이를 통해 다양한 물체의 재질감을 효과적으로 표현할 수 있다.
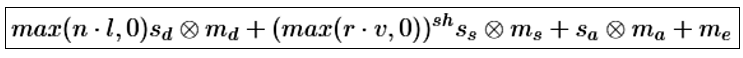
Phong model Equation
1) Diffuse
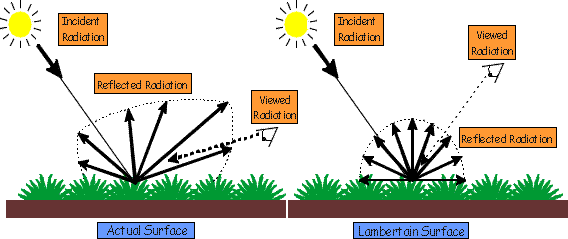
Diffuse Light ( In Lambertian Surface)
디퓨즈 표면은 이상적인 반사 특성을 가지며, 들어오는 빛을 모든 방향으로 균일하게 반사하는데, 이를 램버시안 표면이라고 한다. 이러한 표면에서는 카메라가 어느 방향에서 바라보든 감지되는 빛의 강도가 변하지 않으며, 이는 물체 표면에 도달하는 빛의 양에만 비례한다. 램버시안 반사는 단위 입체각에서 모든 방향으로 균일한 광속을 갖는 특징을 가지며, 반사광의 세기는 표면 법선과 빛 벡터 사이의 각도에 따라 코사인 함수 값으로 변하는 램버트의 코사인 법칙(Lambert's Cosine Law)을 따른다.
물체 표면으로 들어오는 빛의 방향은 빛 벡터 에 의해 정의되며, 표면의 점 에서의 법선 벡터 과 빛 벡터 l 사이의 각도 θ는 입사각(incident angle)이라 한다. 입사각 θ가 작을수록 점 p는 더 많은 빛을 받게 되며, 이는 cos값에 비례한다. 이를 수식으로 표현하면 max(n⋅l,0) 가 되는데, 이는 내적 n⋅l이 음수일 경우 0을 선택하여 물체의 표면이 빛을 받지 않는 영역에서는 조도가 0이 되도록 보장한다. 즉, 점 p가 받는 빛의 강도는 오로지 cosθ값에 의해 결정된다.
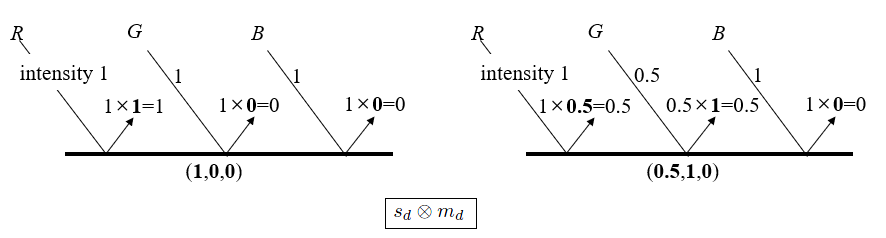
반사되는 빛의 색상 정의
반사되는 빛의 색상은 광원의 색상과 물체의 재질 특성에 의해 결정된다. 여기서 sd는 광원의 RGB 색상을 나타내며, mdm_d 는 물체의 디퓨즈 반사율(diffuse reflectance)로서 물체가 빛을 어느 정도 흡수하고 반사하는지를 결정하는 계수이다. 표기법에서 s는 광원(light source), m 은 물체의 재질(material)을 의미하며, 이를 통해 표면에서 반사되는 빛의 최종 색상이 결정된다.
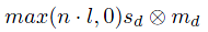
따라서 앞의 식으로 강도를, 뒤의 식으로 색상을 나타낸다.
2) Specular

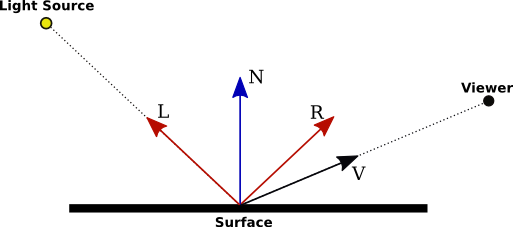
퐁 모델의 스페큘러 항은 물체 표면에서 하이라이트(highlight)를 생성하는 역할을 하며, 이를 계산하기 위해 시선 벡터(view vector)와 반사 벡터(reflection vector)가 필요하다. 시선 벡터 는 물체 표면의 점 p에서 카메라로 향하는 방향을 나타내며, 실제 카메라 시선과 반대 방향으로 정의된다. 반사 벡터 r은 들어온 빛이 입사각 θ와 동일한 각도를 이루며 반사되는 방향을 나타내는 벡터로, 법선 벡터 n과 빛 벡터 l이 이루는 입사각 θ와 n과 r이 이루는 반사각이 동일하다는 성질을 가진다. 벡터 관계를 통해 r을 구할 수 있으며, l이 단위 벡터이므로 r 또한 단위 벡터가 된다.
디퓨즈 반사는 카메라의 위치에 관계없이 일정한 밝기를 보이지만, 스페큘러 반사는 카메라의 위치에 따라 반사광이 보이는 정도가 달라진다. 즉, 하이라이트가 보이는 영역은 반사 벡터 r을 중심으로 한 원뿔 형태로 형성되며, 카메라 방향 벡터 v와 반사 벡터 rr이 유사할수록 더 강한 하이라이트가 관측된다. 표면의 매끈함 정도를 결정하는 shininess 값 sh 이 효과를 조절하는 요소로, r과 v가 일치하면 sh값과 관계없이 최대 하이라이트가 나타나지만, 두 벡터가 조금이라도 다르면 sh값이 클수록 하이라이트가 급격히 감소한다. 즉, 매끈한 표면일수록 하이라이트가 작고 강하게 보이며, 거친 표면일수록 넓게 퍼진 하이라이트가 나타난다.
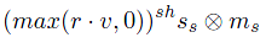
스페큘러 항
스페큘러 항에서 ss는 광원의 색상을, ms는 물체의 스페큘러 반사 계수(specular reflectance)를 의미하며, 디퓨즈 반사와 마찬가지로 max함수를 사용하여 음수 값을 제거해야 한다. 하지만 ms는 디퓨즈 계수 md와 달리 회색조 값으로 설정되며, 이는 물체 표면의 하이라이트가 광원의 색을 반영하도록 하기 위함이다. 예를 들어, 빨간색 금속성 물체에 흰색 광원이 비출 경우, 표면의 기본 색상이 빨간색이라 하더라도 하이라이트 부분은 흰색으로 보인다. 따라서 ms는 회색조 값으로 설정하여 광원의 색상이 얼마나 반사되는지를 조절하며, 이를 통해 더욱 현실적인 반사 효과를 표현할 수 있다.
3) Ambient
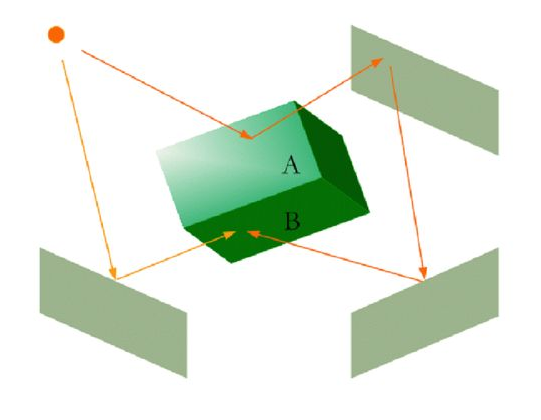
공간 내 다양한 물체에서 반사된 빛은 특정한 방향성을 가지지 않고 모든 방향에서 고르게 퍼지는데, 이를 앰비언트 빛(ambient light)이라 한다. 이는 직접적인 광원이 아닌 간접 조명에 해당하며, 특정한 방향 없이 표면의 점 에 도달한다. 따라서 앰비언트 빛은 표면의 법선 벡터 n에 영향을 받지 않고, 점 p에 도달한 후에도 특정한 방향 없이 균일하게 반사된다. 그 결과, 앰비언트 빛은 카메라의 시선과도 무관하게 일정한 밝기를 제공하며, 광원이 직접 닿지 않는 영역에도 조명이 적용될 수 있도록 해준다.
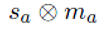
앰비언트 항에서는 sa가 앰비언트 빛의 RGB 색상을, ma가 물체의 앰비언트 반사 계수(ambient reflectance)를 의미한다. 이 항은 공간 내 간접 조명을 표현하는 요소로, 광원이 직접 비추지 않는 부분에도 약간의 조명 효과를 주는 역할을 한다. 즉, 앰비언트 항이 없으면 그림자가 너무 어둡거나 조명이 닿지 않는 부분이 비현실적으로 검게 표현되지만, 이를 통해 최소한의 밝기가 유지되면서 더욱 자연스러운 장면을 연출할 수 있다.

그러나 이 모델은 실세계에서 발생하는 복잡한 간접 조명의 디테일을 완벽하게 표현하기에는 단순화된 방식이다. 예를 들어, 약간의 조명을 받는 주전자는 주변 환경에서 반사된 앰비언트 빛을 받아 일정한 밝기를 유지하지만, 실제 세계에서는 물체 간의 반사와 색 번짐 등 다양한 요소가 존재하기 때문에 보다 정교한 조명 모델이 필요한 것이다.
4) Emissive
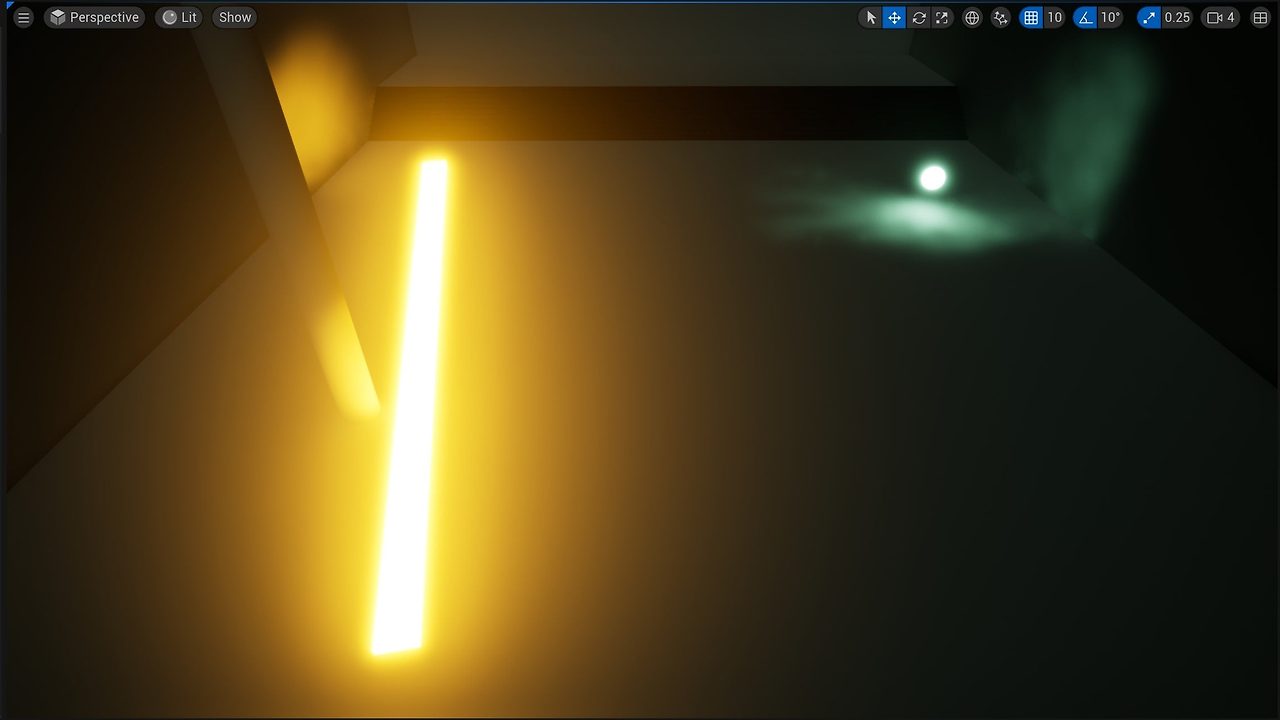
퐁 모델의 발산광(emissive light) 항은 물체 자체가 빛을 내는 경우를 표현하기 위해 사용된다. 그러나 퐁 모델에서 발산광을 가진 물체는 실제 광원으로 취급되지 않으므로, 같은 공간에 있는 다른 물체를 비추는 역할을 하지 못한다. 즉, 발산광을 가지는 물체는 자기 자신을 밝게 보이게 만들지만, 주변 환경에는 영향을 미치지 않는다. 이로 인해 퐁 모델은 광원이 직접 조명을 투사하는 효과만을 고려할 뿐, 복잡한 간접 조명 효과나 발광 물체가 주변 환경을 비추는 현상을 정확하게 표현할 수 없다는 한계를 가진다.
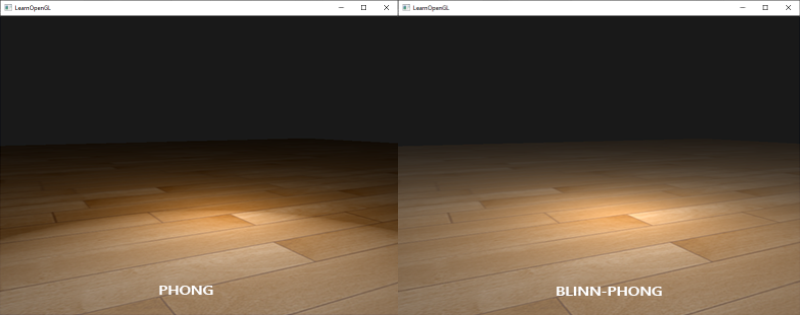
💡 Blinn-Phong

Blinn-Phong 모델은 퐁 모델을 개선한 조명 모델로, 정반사 성분을 계산할 때 반사 벡터 대신 하프 벡터(Half Vector) 를 사용하는 것이 특징이다. 기존 퐁 모델에서는 시선 벡터(View Vector)와 반사 벡터(Reflection Vector) 간의 내적을 사용했지만, Blinn-Phong 모델에서는 시선 벡터 v와 빛 벡터 l의 중간 벡터인 하프 벡터 h를 구한 후, 이를 법선 벡터 n과 내적하는 방식으로 정반사 성분을 계산한다. 이를 통해 보다 부드러운 하이라이트 표현이 가능하며, 특히 높은 광택을 가진 표면에서 계산이 더욱 안정적으로 이루어진다. Blinn-Phong 모델은 퐁 모델보다 효율적이고 현실적인 정반사 효과를 제공하기 때문에 실시간 렌더링에서 자주 사용된다.
💡 Lighting Models

컴퓨터 그래픽에서는 실제 세계의 복잡한 조명 효과를 단순화하여 구현하기 위해 여러 종류의 광원을 사용한다. 대표적인 광원은 다음과 같다.
- Point Light (점광원): 한 지점에서 모든 방향으로 빛을 방출하며, 거리에 따라 빛의 세기가 감소하는 광원이다.
- Directional Light (방향광): 매우 멀리 있는 거대한 광원으로 간주되어 장면 전체에 일정한 방향과 세기의 빛을 제공하는 광원이다.
- Spotlight (스포트라이트): 원뿔 모양의 빛을 방출하여 중심부에서 가장 강한 빛을, 가장자리로 갈수록 약해지는 효과를 주어 특정 영역을 집중적으로 비추는 광원이다.
- Ambient Light (앰비언트 라이트): 실제 광원이 아닌, 장면 전체에 일정하고 변화하지 않는 약한 밝기를 제공하여 기본적인 배경 조명 역할을 하는 가상의 광원이다.
이와 같이 셰이더의 라이팅은 물리적인 빛의 특성과 다양한 광원 모델을 기반으로 현실감 있는 조명 효과를 구현하는 기술이다. 쉽게 말하면, 가상의 카메라가 보는 장면에 빛을 '그리는' 도구로서, 다양한 빛의 성질과 광원 효과를 조합해 실제처럼 느껴지는 이미지를 만들어내는 기술이다.
2. Coloring
2.1 Basic Principles of Color

Computer Graphics Lighting and Colors
빛은 입자성과 파동성을 동시에 가지지만, 색을 표현하는 관점에서는 주로 파동의 특성이 중요하게 작용한다. 빛이 파동의 형태로 전파된다는 것은 특정한 주파수(frequency)를 가지며 진동한다는 것을 의미하며, 이 주파수에 따라 서로 다른 색이 결정된다. 가시광선 영역에서 주파수가 낮은 빛은 빨간색에 가깝고, 주파수가 높은 빛은 보라색에 가까우며, 이를 기반으로 RGB 색 공간과 같은 컬러 모델이 만들어진다. 따라서 컴퓨터 그래픽스에서는 빛의 물리적 특성을 수학적으로 모델링하여 현실적인 조명과 색을 표현하는 기술이 필수적으로 사용된다.
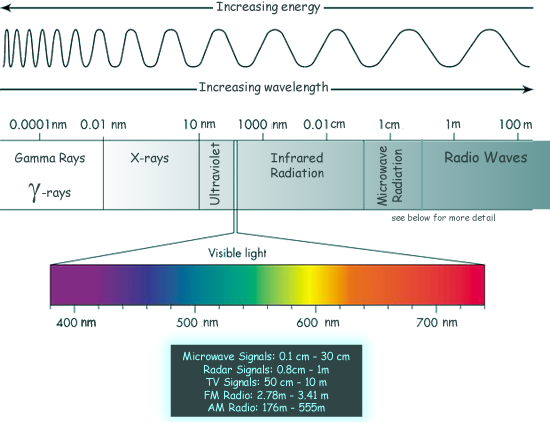
Electromagnetic spectrum
전자기 스펙트럼(Electromagnetic Spectrum)은 다양한 파장의 전자기파를 포함하는 범위를 의미하며, 파장은 진동수와 반비례하고, 에너지는 진동수에 비례하므로 파장이 길수록 에너지는 낮아진다. 빛의 스펙트럼에는 라디오파, 마이크로파, 적외선, 가시광선, 자외선, X-선, 감마선 등이 포함되며, 인간이 볼 수 있는 색은 가시광선 영역에 속한다. 가시광선의 파장은 약 400nm에서 700nm 범위에 있으며, 파장이 길어질수록 보라색에서 시작해 남색, 파랑, 초록, 노랑, 주황, 빨강으로 변화한다.
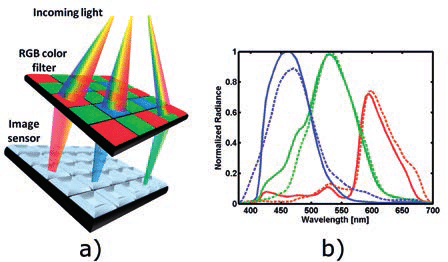
인간의 눈이 색을 인지하는 과정은 수정체가 빛을 모으고 시신경을 통해 신호를 전달하는 방식으로 이루어진다. 시신경은 간상세포(Rod Cells) 와 원추세포(Cone Cells) 로 구성되는데, 간상세포는 명암 감지와 시야 확보를 담당하지만 색을 구별하지 못한다. 반면, 원추세포는 색을 감지하는 역할을 하며, 빨강, 초록, 파랑(RGB) 세 가지 파장에 민감한 세포들이 존재한다. 빛이 들어오면 각 원추세포가 특정 파장의 빛에 반응하여 신호를 생성하고, 뇌가 이 신호를 조합하여 최종적으로 색을 인식한다. 카메라 센서 역시 인간의 눈과 유사한 방식으로 색을 감지하고 처리한다. 대부분의 카메라 센서는 RGB 컬러 필터를 사용하여 빛을 빨강, 초록, 파랑(RGB) 세 가지 기본 색으로 분해하고, 각 색상의 강도를 측정하여 디지털 이미지로 변환한다. 가장 널리 사용되는 컬러 필터 배열은 Bayer 패턴 으로, 인간의 눈이 녹색 빛에 가장 민감하다는 점을 고려하여 녹색 픽셀을 50%, 빨강과 파랑 픽셀을 각각 25% 비율로 배치한다. 하지만 Bayer 패턴의 경우 각 픽셀이 단일 색상 정보를 제공하므로, 최종적으로 전체 이미지의 색을 복원하기 위해 디모자이크(Demosaicing)와 같은 알고리즘을 적용하여 인접한 픽셀의 정보를 조합하는 과정이 필요하다. 이러한 원리를 통해 카메라 센서는 실제 세계의 색상을 디지털 이미지로 변환하여 표현할 수 있다.
💡 Weber's Law
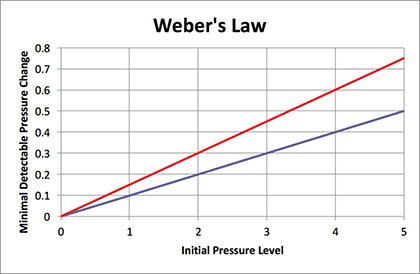
베버의 법칙은 독일 심리학자 베버가 제시한 감각 심리학 법칙으로, 단일 자극과 두 자극 사이의 밝기 차이를 인지하는 데 필요한 최소 변화량을 수학적으로 표현한다. 이 법칙에 따르면, 두 자극의 밝기 차이 ΔI 가 기준 자극의 밝기 에 비례해야만 인간이 이를 감지할 수 있으며, 이를 베버 상수 Δ로 나타낼 수 있다. 즉, 밝기가 높아질수록 더 큰 변화가 있어야만 차이를 인식할 수 있으며, 인간의 눈은 기준 밝기 대비 약 1~2%의 차이를 감지할 수 있다. 이러한 시각적 특성 때문에 디지털 이미지에서 128 또는 256 단계의 밝기 변화가 자연스럽고 부드럽게 보이는 것이다.
예를 들어, 어두운 방에서 촛불 하나가 켜져 있을 때, 추가로 하나의 촛불을 더 밝히면 그 차이를 쉽게 인지할 수 있다. 그러나 이미 100개의 촛불이 켜져 있는 방에서 하나를 더 추가한다고 해도 그 변화는 거의 느껴지지 않는다. 이는 베버의 법칙에 따라 기준 밝기가 증가할수록 변화를 감지하기 위해 필요한 밝기 차이도 커지기 때문이다. 마찬가지로, 디지털 이미지에서 밝기가 낮은 어두운 부분에서는 미세한 밝기 차이도 쉽게 구분되지만, 매우 밝은 영역에서는 동일한 변화량이 적용되더라도 차이가 덜 인식된다. 이러한 원리는 영상 처리 및 디스플레이 기술에서 감마 보정과 같은 기법을 적용하는 데 중요한 역할을 하며, 인간의 시각적 특성을 고려하여 자연스럽고 부드러운 밝기 변화를 제공하는 데 활용된다.
2.2 Color Models
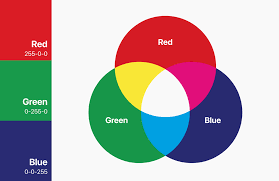
컴퓨터 그래픽스에서 색 공간은 각각의 목적에 맞게 사용되며, 효과적인 색 표현과 처리를 가능하게 한다. RGB 모델은 디지털 디스플레이에서 색을 직접 표현하는 방식으로, 빨강(R), 초록(G), 파랑(B) 세 가지 기본 색을 혼합하여 다양한 색을 생성하는데 적합하다. 그러나 RGB는 저장 및 전송 효율성이 낮고, 밝기와 색 정보를 따로 분리하기 어려운 단점이 있다.
2.2.1 HSV
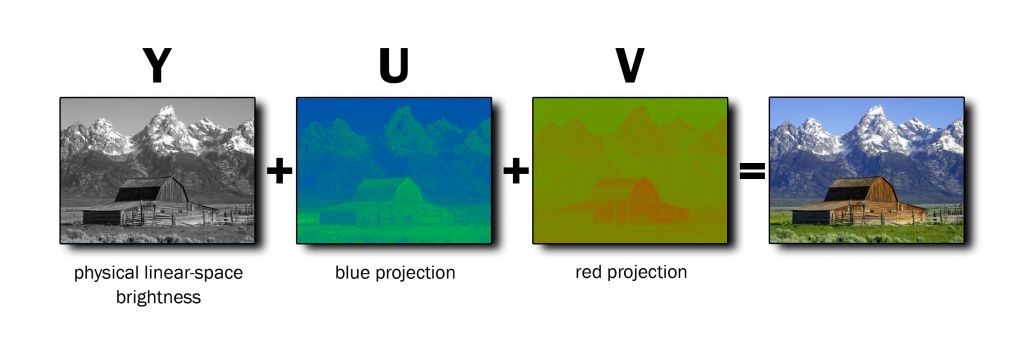
YUV
빛의 색을 표현할 때 입력과 출력은 주로 RGB 모델을 사용하지만, 영상 처리에서는 색 정보를 보다 효율적으로 다루기 위해 밝기(Luminance)와 색상(Chrominance)으로 분리하여 표현하는 YUV 모델을 사용한다. YUV 모델은 루미넌스(Y)와 크로미넌스(U, V)로 구성되며, 루미넌스(Y) 는 영상의 밝기 정보를 담당하고, 크로미넌스(U, V) 는 색 정보를 나타낸다. 인간의 시각은 색의 변화보다 밝기에 더 민감하기 때문에, YUV 모델을 활용하면 밝기 정보를 유지하면서 색 정보의 크기를 줄여 효율적인 저장과 전송이 가능하다.

YUV 모델에서 루미넌스(Y) 는 흑백 영상의 밝기 정보를 나타내며, 0(검정)에서 255(흰색) 범위를 가진다. 반면, 크로미넌스(U, V) 는 색 정보를 저장하는데 사용되며, 각각 -128에서 127까지의 범위를 갖는다. YUV 모델은 밝기 정보를 한 번만 저장하고 색 정보(U, V)는 절반만 저장하는 방식이므로, RGB 모델보다 저장 공간을 절약할 수 있으며, 색 변환 및 압축 과정에서도 유리하다. 이는 TV 방송, 비디오 코덱, 이미지 압축 기술(JPEG) 등에서 널리 활용되며, 밝기 변화에 영향을 받지 않는 색 재현을 가능하게 한다.
2.2.3 HSV

HSV
HSV 모델은 색을 표현하는 방식으로 색조(Hue), 채도(Saturation), 명도(Value) 세 가지 요소를 사용한다. 이는 원기둥(Cylindrical) 형태의 색 공간으로 구성되며, 인간의 색 인식 방식과 유사하게 색을 조작할 수 있어 직관적인 색 조정이 가능하다. 색조(Hue) 는 빛의 파장에 해당하며, 0°는 빨강, 120°는 초록, 240°는 파랑을 의미한다. 채도(Saturation) 는 색의 순도를 나타내며, 0%는 회색(무채색), 100%는 가장 선명한 색을 의미한다. 명도(Value) 는 색의 밝기를 나타내며, 0%는 검정, 100%는 흰색을 의미한다.
HSV 모델은 색상, 채도, 밝기를 개별적으로 조절할 수 있어 이미지 편집, 조명 효과 조절, 그래픽 디자인 등의 분야에서 널리 사용된다. 예를 들어, 명도를 조절하면 색상의 변화 없이 어두운 환경에서도 색을 유지할 수 있으며, 채도를 조정하면 같은 색상의 다양한 톤을 생성할 수 있다. 그러나 HSV 모델은 RGB 모델과 직접적으로 호환되지 않으며, 비선형적인 색 공간을 가지므로 색상 변환 과정에서 왜곡이 발생할 수 있다는 단점이 있다. 그럼에도 불구하고, 색을 보다 직관적으로 다룰 수 있다는 장점 때문에 그래픽 디자인 및 색상 조정 작업에서 중요한 역할을 한다.
따라서 RGB는 디스플레이 출력에, YUV는 영상 압축 및 전송에, HSV는 색상 조정과 편집에 최적화되어 있어 그래픽스에서 각각 중요한 역할을 한다.
3. Shading

Flat Shading, Gouraud Shading, Phong Shading
컴퓨터 그래픽스에서 조명과 음영(Shading) 처리는 3D 객체를 더욱 현실적으로 표현하는 핵심 요소이다. 3D 모델은 다각형(주로 삼각형)의 조합으로 이루어져 있으며, 각 다각형이 빛을 어떻게 반사하는지에 따라 최종적인 화면 출력이 결정된다. 단순히 객체의 형태를 렌더링하는 것만으로는 사실적인 표현이 어렵기 때문에, 다양한 Shading 기법을 통해 표면의 부드러움과 빛의 반사 효과를 조정하여 현실감을 높인다. Shading 기법은 크게 Flat Shading, Smooth Shading(Gouraud Shading, Phong Shading)으로 나뉘며, 각각 성능과 품질의 균형을 맞추기 위해 사용된다.
3.1 Flat Shading
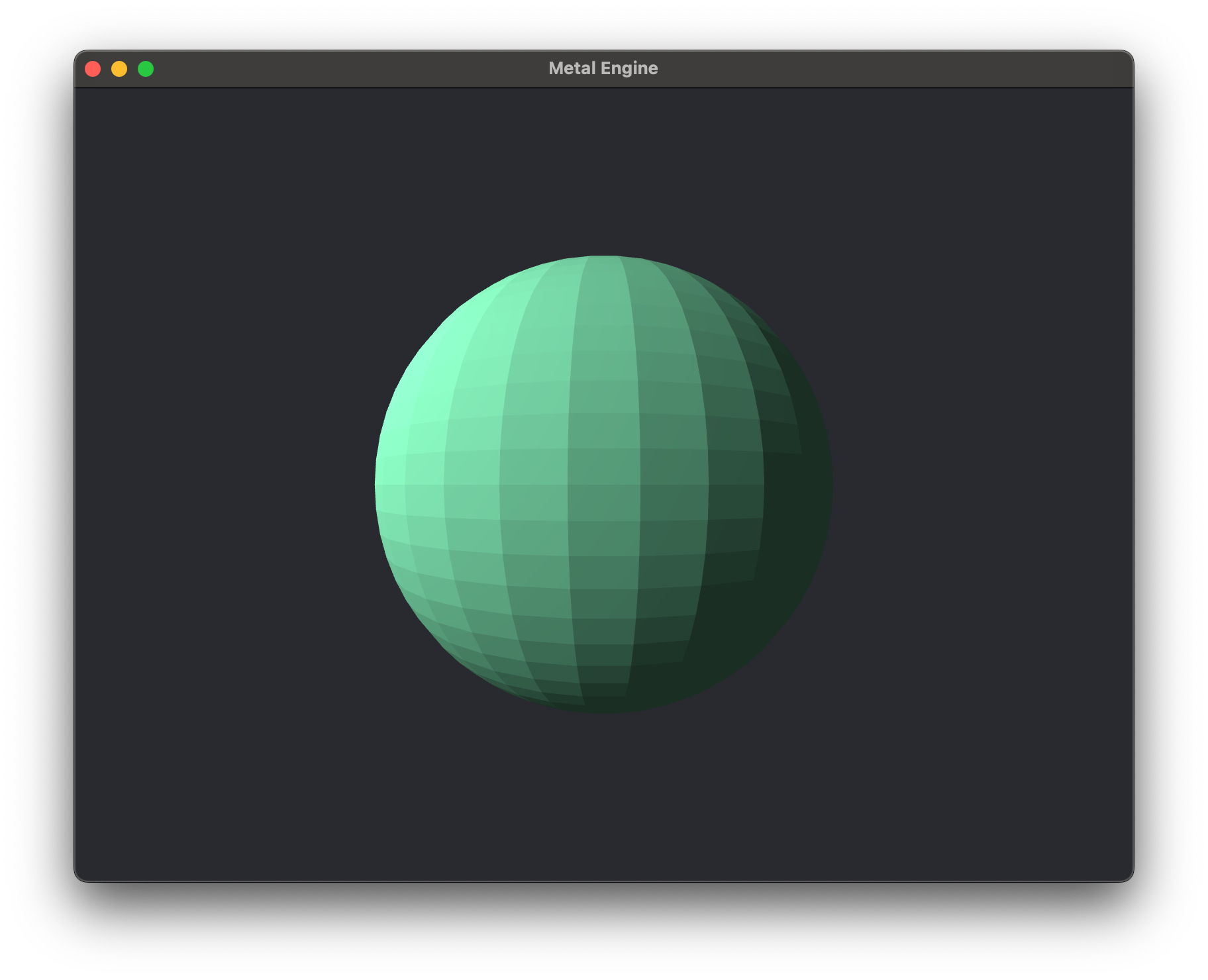
Flat Shading은 가장 기본적인 Shading 기법으로, 다각형(Polygon) 하나당 하나의 면 법선(Face Normal)을 사용하여 조명을 계산한다. 즉, 하나의 다각형에 대해 한 번만 색상을 계산하며, 해당 다각형에 속하는 모든 픽셀은 동일한 색상을 갖는다. 이 방식은 계산량이 적어 매우 빠르게 렌더링할 수 있지만, 곡면을 표현할 때 각진 형태가 두드러지는 단점이 있다. 따라서 낮은 해상도의 모델이나 단순한 형태의 물체에는 적합하지만, 부드러운 표면을 요구하는 장면에는 적절하지 않다.
3.2 Smooth Shading
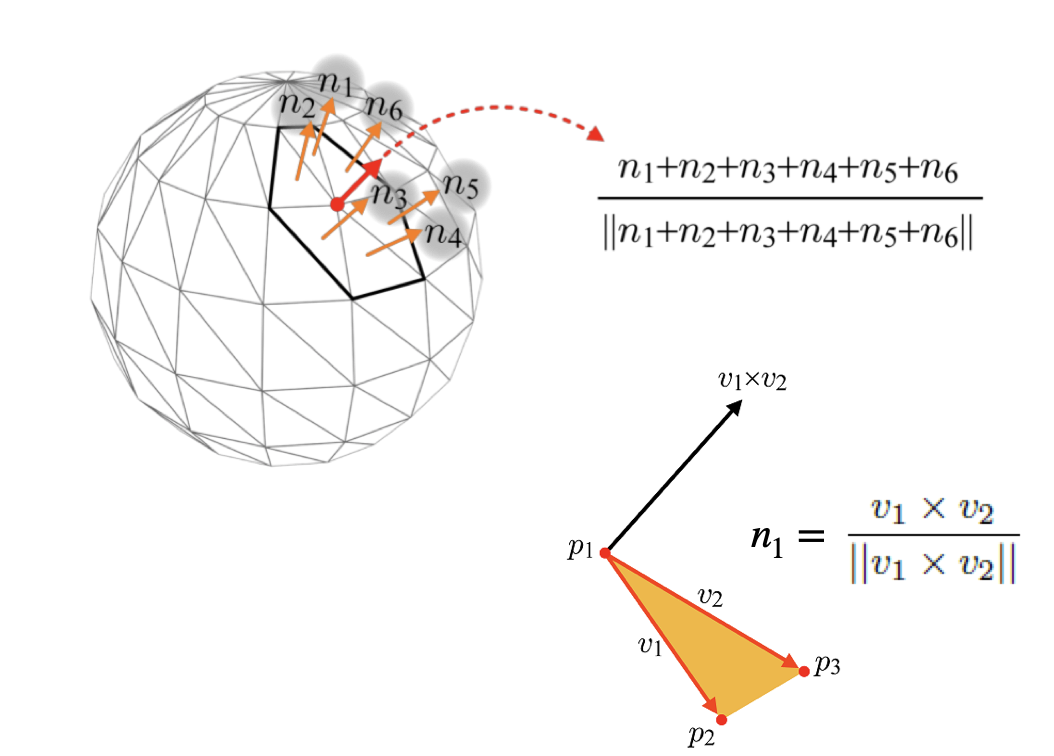
Smooth Shading은 Flat Shading의 단점을 보완하여, 인접한 다각형 사이의 색상이 부드럽게 변화하도록 하는 기법이다. 이를 위해 각 면마다 하나의 Face Normal을 사용하는 대신, 각 꼭짓점(Vertex)마다 개별적인 Vertex Normal을 사용한다. 한 점에서의 Vertex Normal은 해당 꼭짓점과 연결된 모든 다각형의 Face Normal을 평균 내어 단위 벡터로 정규화한 값이다. 이렇게 하면 표면이 보다 자연스럽게 보이며, 빛의 반사도 부드럽게 표현할 수 있다. Smooth Shading의 대표적인 방식으로는 Gouraud Shading과 Phong Shading이 있으며, 두 방식은 색상과 법선 벡터를 어떻게 보간(Interpolation)하는지에 따라 차이가 있다.
3.2.1 Gouraud Shading
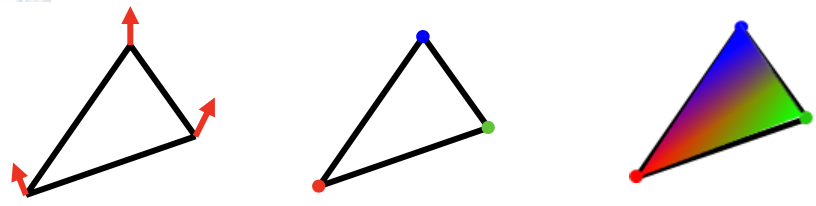
Gouraud Shading
Gouraud Shading은 각 꼭짓점에서 먼저 조명 계산을 수행한 후, 삼각형 내부의 픽셀 색상을 보간하여 결정하는 방식이다. Barycentric Interpolation을 사용하여 꼭짓점 색상을 내부 픽셀로 확장하므로, 비교적 빠르게 렌더링할 수 있으며 표면이 부드럽게 표현된다. 그러나 반사광(Specular Highlight)이 제대로 표현되지 않거나 흐려지는 문제가 발생할 수 있다. 특히, 작은 크기의 빛 반사나 강한 광원 효과가 평균화되어 사라지는 경우가 많아, 하이라이트 표현이 중요한 장면에는 적합하지 않을 수 있다. 다각형의 개수를 늘려 이러한 문제를 보완할 수 있지만, 이는 계산량 증가로 이어진다.
3.2.2 Phong Shading
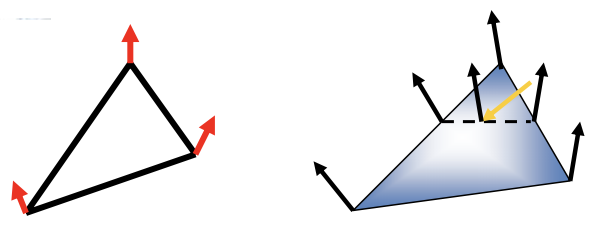
Phong Shading
Phong Shading은 Gouraud Shading과 달리, 꼭짓점에서 직접 색상을 계산하는 것이 아니라, 꼭짓점에서 보간된 Vertex Normal을 기반으로 각 픽셀에서 조명 계산을 수행하는 방식이다. 이 과정에서 Barycentric Interpolation을 이용하여 삼각형 내부의 각 픽셀별 Normal을 보간한 후, 해당 Normal을 기반으로 조명 모델을 적용하여 색상을 결정한다. 결과적으로 보다 정밀한 조명 효과를 얻을 수 있으며, 특히 하이라이트 영역이 자연스럽게 표현된다. 그러나 이 방식은 픽셀 단위로 조명을 계산해야 하기 때문에 계산량이 많아 성능 부담이 크다.

이러한 셰이딩과 라이팅 모델의 이해는 개발자가 사실적인 그래픽을 구현하는 데 필수적이다. 셰이더는 단순한 색상 계산을 넘어 빛과 물체의 물리적 상호작용을 시뮬레이션하여 가상의 세계를 더욱 현실적으로 표현한다. 이를 위해 Phong, Blinn-Phong과 같은 반사 모델과 Flat, Gouraud, Phong Shading 등의 셰이딩 기법을 적절히 활용해야 하며, 실시간 렌더링에서는 성능과 품질의 균형을 고려한 최적의 조명 모델을 선택하는 것이 중요하다. 또한, RGB, YUV, HSV 등의 색상 모델을 이해하면 그래픽 최적화와 색 보정이 가능해 보다 자연스럽고 효율적인 화면을 구현할 수 있다. 개발자는 이러한 개념을 기반으로 현실감 있는 조명과 셰이딩을 설계하고, 최적화 기법을 적용하여 실시간 그래픽 성능을 극대화할 수 있다.
'Computer Graphics > Graphics Theory' 카테고리의 다른 글
| Computer Graphics [6] : 그래픽스 응용 (Graphics Applications) (1) | 2025.02.02 |
|---|---|
| Computer Graphics [5] : 카메라 시점 (Camera View) (0) | 2025.02.02 |
| Computer Graphics [3]: 텍스쳐 (Texture) (1) | 2025.01.11 |
| Graphics Theory [7] : 렌더링 파이프라인 (Rendering Pipeline) (0) | 2024.10.08 |
| Computer Graphics [2]: 변환 (Transformation) (2) | 2024.09.18 |