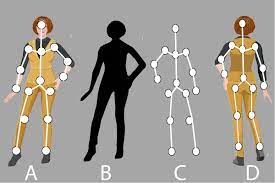
실시간 캐릭터 애니메이션을 위해서는 대체로 캐릭터의 골격(Skeleton)을 이용한다. 골격은 다수의 뼈(Bone)로 구성된 관절체(Articulated body)이다.
Animation
1. Character Mesh and Skeleton
Character Mesh and Skeleton
(a) Default Pose of the Character Mesh : 모든 캐릭터를 애니메이션하기 위한 시작점으로 bind pose 또는 rest pose라고 불린다.
(b) Skeleton Templates : 3ds Max에서 제공하는 바이페드(biped)라는 기본 골격이다.
(c) Customization : 높은 커스터마이징이 가능하다. 예를 들어, 3ds Max에서 기본 스켈레톤을 편집하여 더 간단한 Rig를 위해 네 개의 척추를 단일 척추로 결합하는 등 캐릭터에 맞게 수정할 수 있다.
(d) Embedding the Skeleton : 스켈레톤을 메쉬에 연결한 후에는 스켈레톤이 캐릭터 메쉬 내부에 위치하도록 숨긴다.
(e) (f) Fitting to the Default Pose : 스켈레톤을 캐릭터 메쉬의 기본 포즈 (default pose)에 맞추는 작업이다. 이 과정을 통해 스켈레톤의 각 관절 위치가 메쉬의 해당 신체 부위와 일치하도록 미세 조정한다.
Skeletal hierarchy
스켈레톤은 개별적인 뼈들이 서로 연결되어 계층 구조를 형성한다. 이 계층 구조에서 뼈들은 부모-자식 관계를 가지고 있으며, 이를 통해 전체적인 신체 움직임을 제어한다. 스켈레톤에서 가장 상위 레벨의 객체는 일반적으로 골반(pelvis)뼈이다. 골반은 루트 노드 (root node) 역할을 하며, 전체 계층 구조의 기반이 된다. 이 하위 레벨의 뼈들은 골반의 움직임에 따라 영향을 받고 각 레벨의 뼈들은 다시 자식 노드 (child node)를 가지며, 계층 구조를 통해 서로 연결되어 전체적인 신체 움직임을 가능하게 한다.
Local Motion : 각 뼈는 자체적인 좌표계를 가지고 있으며, 이를 기반으로 독립적인 로컬 움직임을 정의한다. 일반적으로 뼈의 움직임은 주로 회전에 국한된다.
Cascading Effects : 뼈들은 부모-자식 계층 구조 (hierarchical structure)를 형성한다. 이 구조에서 부모 뼈의 움직임은 모든 자식 뼈 (연결된 하위 뼈)에게 영향을 미친다. 이를 계층적 영향 (cascading effects)이라고 부른다.
Space Change between Bones
Joint
뼈는 관절(Joint)로 연결되어 있다. 정점 vu, vf, vh는 각각 위팔, 아래팔, 손에 속한다. 한 뼈가 움직이면 그 뼈에 속한 정점도 움직인다. 한 물체는 자신의 오브젝트 공간과 결합되어 있다. 아래팔과 그 오브젝트 공간은 항상 같이 움직이므로, 오브젝트 공간에 정의된 vf는 항상 아래팔과 같이 움직이게 된다.
- 캐릭터의 기본 포즈에서 모든 꼭짓점들은 캐릭터의 좌표계(Character Space)에서 정의된다.
- 각 뼈의 로컬 좌표계(Bone Space)에서 꼭짓점의 위치를 정의한다.
- 뼈와 관절의 움직임을 적용하여 꼭짓점들을 월드 좌표계로 변환한다.
캐릭터의 객체 공간에서 꼭짓점 vf의 좌표가 (64, 32, 32)라고 가정한다. 같은 꼭짓점이 팔뚝의 객체 공간에서는 (2, 0, 0)으로 정의될 수 있다. 이렇게 두 가지 공간을 이용하여 꼭짓점들을 정의하고 변환함으로써, 캐릭터의 움직임을 자연스럽게 구현할 수 있다. 뼈와 관절 사이의 관계를 통해 각 뼈의 로컬 좌표계에서 월드 좌표계로 변환하는 과정을 거치게 된다.
캐릭터 메시의 모든 정점이 정의되어 있는 공간을 캐릭터 공간이라 부르고 드레스 포즈에 골격이 맞춰지면, 캐릭터 공간의 각 정점은 자신이 속한 뼈의 오브젝트 공간으로 변환되어야 하는데, 이를 간단히 뼈 공간이라 부른다.아래팔 공간에서 (2,0)의 좌표를 가지는 vf를 캐릭터 공간으로 변환할 것인데, 이는 역(inverse)을 취하면 바로 우리가 원하는 변환을 얻게 된다.
vf는 위 행렬 $Mf,p에 의해 위팔 공간으로 변환될 수 있다. Mh,p가 Mf,p와 결합되어 손에 속하는 정점을 조부모인 위팔 공간으로 변환한 것
맨 위의 그림 (f)에서와 같이 드레스 포즈에 골격이 맞춰지면, 부모와 자식 뼈 사이의 상대적인 위치와 방향이 결정된다. 한 뼈에 속한 정점을 그 부모의 뼈 공간으로 변환하는 것을 우리는 부모 변환(to-parent transform)이라 부른다. 아래팔의 부모 변환 행렬을 Mf,p 이라 표기하자. 아래팔에서 위팔로의 공간 이전(Space change)을 의미하는 Mf,p는 위팔 좌표계를 아래팔 좌표계에 포개는 행렬과 같다. 이 사실을 일반화하면, 한 뼈의 정점이 주어졌을 때 부모 변환 행렬을 계속 결합하면 골격 계층 구조의 어떤 조상이든지 그것의 뼈 공간으로 정점을 변환할 수 있음을 알 수 있다.
Bone Space to Character Space
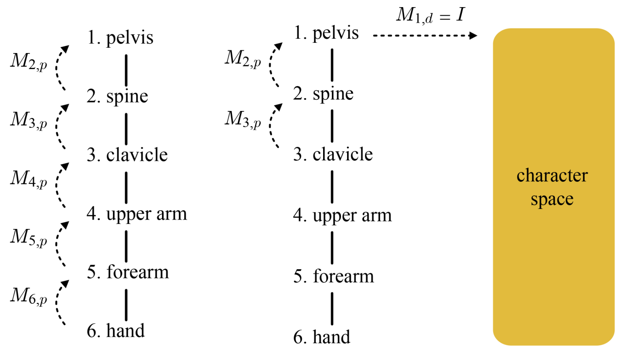
쇄골 공간에서 캐릭터 공간으로 변환
골반(pelvis)은 1, 척추(spine)는 2와 같은 일련 번호로 부르자. 드레스 포즈의 골격이 주어지면, 각 뼈 공간에서 캐릭터 공간으로의 변환을 결정할 수 있다. 이 행렬을 M_i,d로 표기하자. (i는 뼈의 일련번호를, d는 드레스 포즈를 의미한다) 골반은 루트 노드이므로, 골반 공간은 캐릭터 공간과 동일하다고 간주하자. 따라서 M1,d는 단위 행렬(I)이다. 척추 공간에서 캐릭터 공간으로 변환하는 행렬 M_2,d를 구해보면 다음과 같이 두 개 행렬의 결합으로 정의된다.
M_2,d = M_1,d M_2,p
즉 척주의 정점은 M_2,p에 의해 척추의 부모인 골반의 뼈 공간으로 우선 변환되고, 그 다음 M_1,d에 의해 캐릭터 공간으로 변환된다.

위는 뼈 공간에서 캐릭터 공간, 아래는 캐릭터 공간에서 뼈 공간
드레스 포즈 골격이 주어지면, 각 뼈의 부모 변환 행렬 $M_i,p$가 즉시 결정된다. 이는 M-1_i,p이 즉시 결정된다는 뜻이기도 하다. 이런식으로 골격 계층을 거슬러 올라가 보면 우리에게 궁극적으로 필요한 것은 루트 노드인 골반의 M-1_i,d임을 알 수 있다. 다행히 M-1_i,d은 단위 행렬이다. 따라서, M-1_i,d부터 시작해서 골격 계층 구조를 따라 '위에서 아래로 내려가면서' 모든 뼈의 M-1_i,d을 구할 수 있다.
2. Forward Kinematics
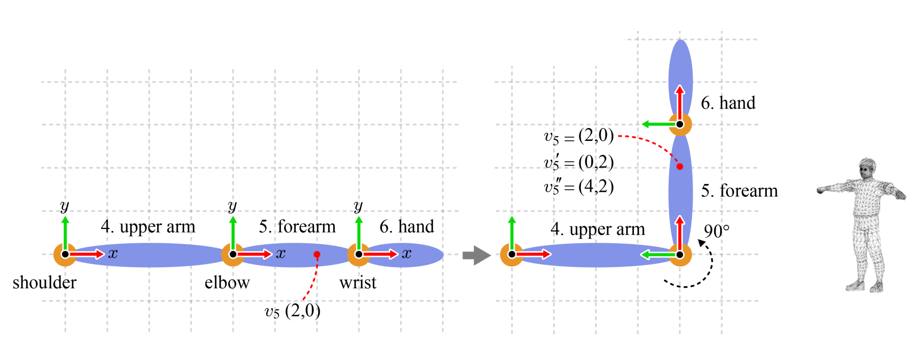
정기구학, 왼쪽 - 드레스 포즈, 오른쪽 - 애니메이션 포즈
각 정점은 자신이 속한 뼈에 의해 움직이는데, 그림은 아래팔(foream)이 회전함에 따라 v_5도 회전한 것을 보여준다. 이렇게 애니메이션이 완료된 정점을 렌더링에 사용하기 위해서는 이를 다시 캐릭터 공간으로 변환해야 한다. 그래야 애니메이션 포즈의 캐릭터 전체가 GPU 파이프라인을 따라 월드 변환, 뷰 변환 등을 거쳐서 최종적으로 스크린에 렌더링될 것이다.
- v_5에 애니메이션을 적용
- 그 결과를 캐릭터 공간으로 옮기는 변환이 필요하다. 이를 M_5,a라 표기하자.
그림에서 아래팔은 90도 회전했다. 이는 아래팔의 뼈 공간의 원점인 팔꿈치를 중심으로 한 회전이다. 이러한 지역적인(local) 특성을 반영하여 이를 지역 변환(local transform)이라 부르자. 인체구조상 변환은 회전만 가능하다. 2차원 동차 좌표계에서의 회전 행렬은 다음과 같다.
아래팔이 회전해도 v_5는 아래팔 공간에서 (2, 0)이라는 좌표를 그대로 유지한다. 반면 v_5'는 '회전되기 전의' 아래팔 공간을 기준으로 하는 좌표이다.

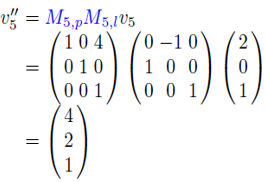
v_5'는 M_5,p에 의해 위팔 공간으로 변환된다.
그런데, '회전되기 전의' 아래팔과 위팔 사이의 관계는 M_5,p(M_f,p)에 의해 정의되었다. 따라서, v_5'는 M_5,p에 의해 위팔 공간으로 변환된다. 관절체 애니메이션에서 모든 뼈는 회전이 가능하다. 즉, 아래팔뿐 아니라 위팔도 회전할 수 있다. (1) 위팔에 속한 정점에 애니메이션을 적용하고, (2) 그 결과를 캐릭터 공간으로 옮기는 변환"을 M_4,a라 표기하자. 그러면 M_5,a를 정의할 수 있다.

M_5,pM_5,l$에 의해 아래팔 공간에서 위팔 공간으로 옮겨지고, $M_4,a$에 의해 캐릭터 공간으로 변환되는 것이다. 골격 계층 구조를 생각해보면 다음과 같이 일반화 될 수 있다.

M_i,a계산을 위해서는 M_i-1,a만 있으면 된다. 그런데 M_i-1,a 계산을 위해서는 M_i-2,a가 필요하다. 이런식으로 골격 계층을 거슬러 올라가 보면 우리에게 궁극적으로 필요한 것은 루트 노드인 골반의 M_1,a임을 알 수 있다.

애니메이션 포즈에서 각 뼈 공간에서 캐릭터 공간으로의 변환
(pelvis) $M_1,a$에 애니메이션을 따로 적용할 필요가 없다. 왜냐하면 월드변환으로 대체된다. root니까 월드 공간에서 캐릭터의 위치와 방향을 정하기 위해 월드 변환이 필요할 텐데, 이 월드 변환은 골격의 루트 노드인 골반(pelvis)을 기준으로 정한다. M_1,a$는 단위 행렬이고, 단위 행렬인 $M_1,a$부터 시작해 골격 계층 구조를 따라 '위에서 아래로 내려가면서' 각 뼈마다 일반화된 식을 사용해 $M_i,a$를 계산하면 된다.

$v$와 $v'$는 모두 캐릭터 공간에서 정의되었는데, 매 프레임 $v'$가 갱신된다.
드레스 포즈 골격이 결정되면, 골격 계층 구조를 따라 '위에서 아래로 내려가면서' 각 뼈마다 $M_i,d^-1$을 계산한다. 이는 단 한번 계산된다. 한편, 애니메이션 포즈가 결정되면, 골격 계층 구조를 따라 역시 '위에서 아래로 내려가면서' 각 뼈마다 $M_i,a$를 계산한다. 이는 모든 애니메이션 포즈에서, 즉 애니메이션의 각 프레임마다 반복된다. 드레스 포즈에서 정점의 캐릭터 공간좌표를 $v$로 표기하자. 이는 우선 $M_i,d^-1$에 의해 해당 뼈 공간으로 변환되고, $M_i,a$에 의해 애니메이션되고 캐릭터 공간으로 변환된다. 이 정점을 $v'$라 표기하자.

$v'$
이렇게 얻어진 $v'$들을 모아 렌더링하면 애니메이션 포즈의 캐릭터를 얻게 된다.
이렇게 모든 뼈의 변환을 계산하여 관절체 전체의 모습을 결정하는 것을 정기구학(forward kinematics 혹은 direct kinematics)이라고 부른다.
3. Skinning
캐릭터의 폴리곤 메시를 피부(skin)라고도 부르는데, 이 챕터는 골격 움직임에 따라 어떻게 피부를 부드럽게 변형하는지 다룬다.

스키닝 애니메이션 - 피부 위의 정점(a) / 블렌딩을 수행하지 않은 경우(b)

스키닝 애니메이션 - 블렌딩 가중치(c) / 블렌딩을 수행한 경우(d)
(b)는 a가 위팔에 속하고 b와 c는 아래팔에 속한다고 가정했을때, 두 팔이 회전했을 때의 결과를 보여준다. 결과인 변형된 피부는 부드럽지 않다. 이러한 문제는 한 정점은 오직 하나의 뼈에 속한다는 제약 때문에 문제가 발생한 것 이다. 여러 개의 뼈가 한 정점에 영향을 주도록 하고 그 결과를 블렌딩(blending)하면 이 문제는 상당히 완화될 수 있다. 각 뼈가 한 정점에 얼마나 영향을 주는지 미리 정해줘야 하는데, 이를 블렌딩 가중치(blending weight) 혹은 간단히 가중치라 부른다. (d)를 보면 $a_u'$와 $a_f'$에 각각 0.7과 0.3의 가중치를 곱해 더한 것이 $a'$이다.
즉 가중치를 이용해 $a_u'$와 $a_f'$를 선형보간한 것이다. $c'$도 마찬가지다. 이 3개의 정점을 연결하면 (b)보다 훨씬 부드러운 피부를 얻게 된다. 이러한 기법을 스키닝(skinning) 혹은 정점 블렌딩(vertex blending)이라 부른다.

정점 블렌딩. (a) 하나의 정점은 두 개의 뼈 공간에서 서로 다른 좌표($v_5$와 $v_6$)를 가진다. (b) 애니메이션 포즈에서 $v_5$와 $v_6$는 각기 다른 캐릭터 공간 좌표를 가지게 되는데, 이를 블렌딩하여 최종 위치를 결정한다.

$v_5$와 $v_6$
$v$는 드레스 포즈의 캐릭터 공간에서 정의된 정점이고, v는 $M_6,d^-1$에 의해 아래팔 공간으로 변환된 것을 $v_5$로 표기한다.

$v_5$와 $v_6$는 각각 $M_5,a$와 $M_6,a$에 의해 애니메이션되고 캐릭터 공간으로 변환된 후, 미리 정의된 가중치 $w_5$와 $w_6$를 사용해 블렌딩되고 결과는 위와 같다. 한 정점에 영향을 주는 뼈들과 그 가중치는 애니메이션 과정 전체에 걸쳐 일정하게 유지되는데, m개의 뼈가 한 정점에 영향을 준다고 가정할때 위의 식은 다음과 같이 일반화된다.

일반화된 식

스키닝 알고리즘의 입력 및 작동 원리. 팔레트 인덱스와 가중치는 정점별로 고정되어 있다. 스키닝 알고리즘은 드레스 포즈의 $v$를 애니메이션 포즈의 $v'$로 변환한다.
위의 그림은 일반화 된 식이 어떻게 구현되는지 보여준다. 야구 선수 캐릭터의 골격은 20개의 뼈를 가진다. 따라서 애니메이션 과정의 매 프레임마다 20개 M_i를 갱신해야 한다. 이는 행렬 팔레트(matrix pallette)라 불리는 테이블에 저장된다.
드레스 포즈의 한 정점 v를 보면 v에 영향을 미치는 뼈의 인덱스는 0, 2, 7, 18이다. 실제로 정점 v에 영향을 미치는 뼈는 4개이며, M_0, M_2,M_7, M_18 네 개의 행렬에 의해 변환되고 결합된다. 그 결과가 바로 v'이다. 일반적으로 스키닝 알고리즘은 정점 쉐이더로 구현된다. 정점 쉐이더에게 행렬 팔레트는 유니폼으로 제공되지만, 팔레트 인덱스와 블렌딩 가중치는 정점 위치, 노멀, 텍스처 좌표 등과 함께 정점 배열에 저장된다.이들은 모두 정점 쉐이더에게 애트리뷰트로 제공된다.
7. Object Picking
1. Screen - Space Object Manipulation
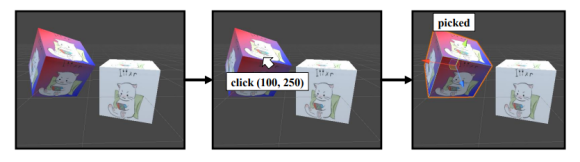
Object Picking
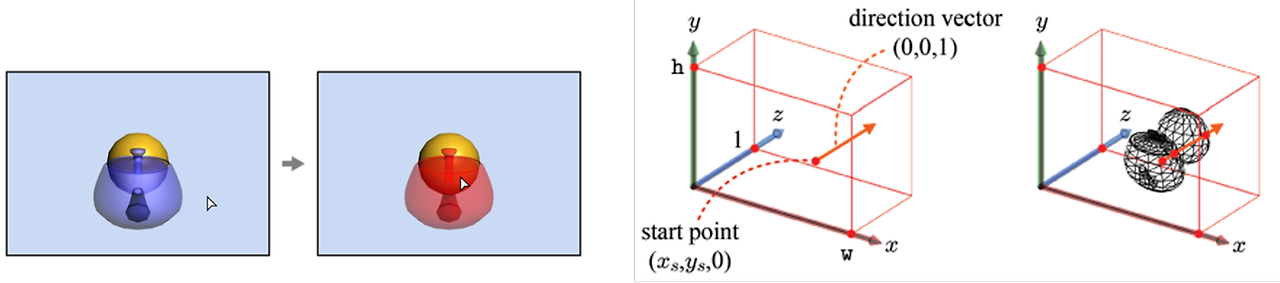
화면상의 클릭과 Screen space에서의 클릭한 지점 start point, z축 방향의 direction vector
화면 상에 어떤 Object를 클릭했을 때, 그 Object가 선택된다. 이때 사용자가 클릭한 것은 지금 보고 있는 모니터, Screen space에서 클릭을 한 것이다. 하지만 스크린 공간에는 Object라는 개념이 없고 단지 개별적인 pixel값만 존재한다. 클릭을 통해 해당 object와 상호작용 하려면 가장 먼저 해야할 일은 클릭한 지점 (x, y,0)에서 z 축으로 뻗는 ray-object(direction vector) 벡터를 만드는 것이다. 이는 같은 선상의 z 축을 통과한다. 이 ray-object가 아래 오른쪽 그림과 같이 처음 맞닿는 object에 닿으면 그 object가 클릭했을 때 골라지는 object임을 직관적으로 우리는 알 수 있다.
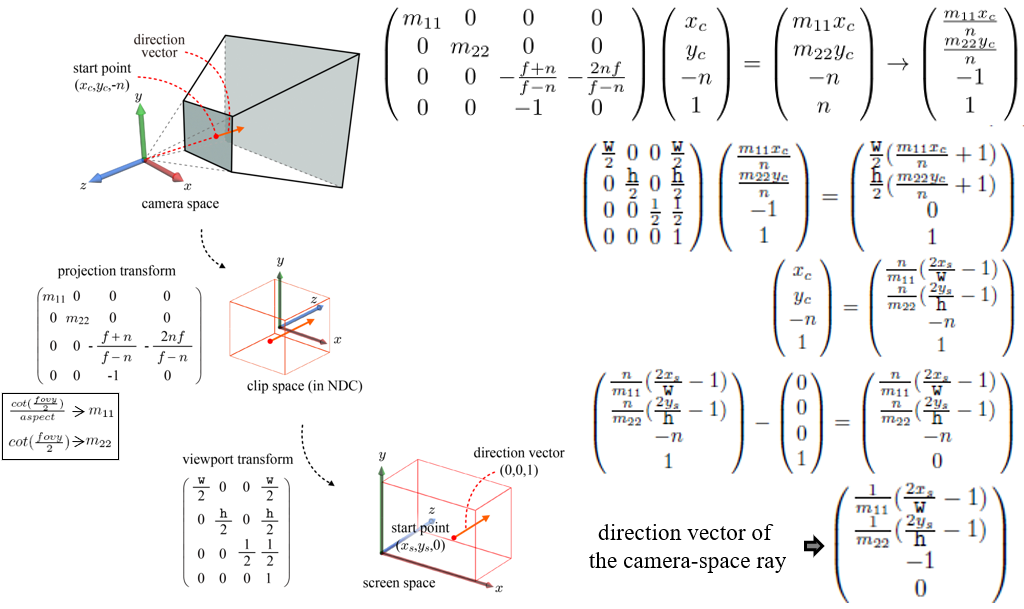
스크린 공간 광선의 시작점은 카메라 공간의 (x_c, y_c, -n)으로 변환되는데, x_c와 y_c는 투영 변환과 뷰포트 변환을 사용하여 계산할 수 있다. 한편, 카메라 공간의 원점과 광선의 시작점을 잇는 벡터를 카메라 공간 광선의 방향 벡터로 설정할 수 있다.
카메라 공간 광선 역시 그 자신의 시작점과 방향 벡터로 정의된다. 그림과 같이 뷰포트의 앞면은 뷰 프러스텀의 전방 평면(near plane)에 해당되므로, 뷰포트 앞면에 놓인 시작점은 카메라 공간의 전방 평면으로 변환된다. 전방 평면의 z좌표가 -n이므로, 카메라 공간 광선의 시작점은 (x_c, y_c, -n)으로 나타낼 수 있다.

투영 변환 행렬을 (x_c, y_c, -n)에 적용하자.
위의 식 결과 뷰포트 행렬에 의해 스크린 공간으로 변환된다.
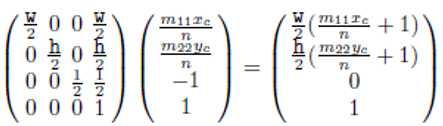
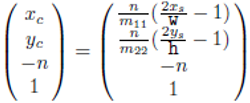
스크린 공간에서의 카메라 공간 광선의 시작점
위 식의 x좌표는 x_s와 같고 y좌표는 y_s와 같다는 사실을 이용하면 x_c와 y_c를 계산할 수 있다. 즉 스크린공간에서 카메라 공간 광선의 시작점은 아래 그림처럼 얻어진다.
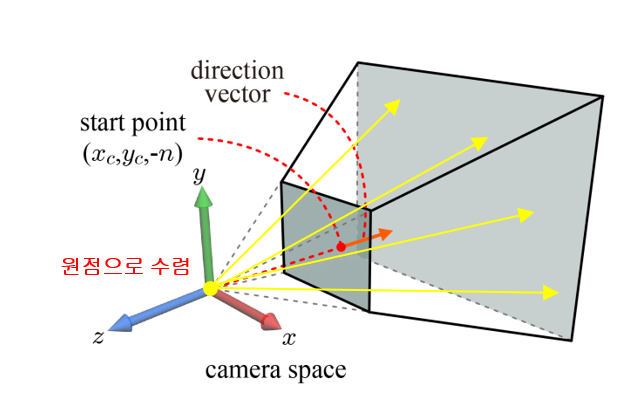
카메라 공간 광선을 뒤로 늘이면 원점에 닿게 된다.

스크린 공간 광선의 방향 벡터
다음은 방향 벡터다. 뷰프러스텀은 카메라 공간의 원점으로 수렴하는 투영선들의 집합이다. 따라서, 카메라 공간 광선을 뒤로 늘이면 원점에 닿게 될 것이다. 원점과 광선의 시작점을 연결한 벡터는 위 그림과 같다.
12.1.3 오브젝트 공간 광선
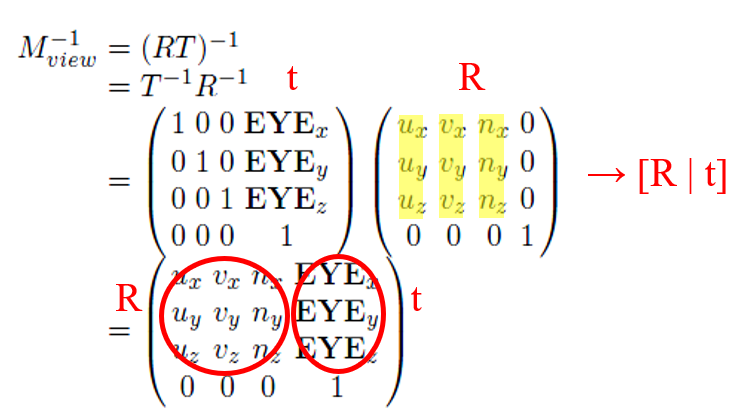
앞 절에서 계산된 카메라 공간 광선을 이제 월드 공간으로, 그 다음에 오브젝트 공간으로 변환해야 한다. 먼저, 월드 공간으로의 변환을 위해서는 뷰 변환의 역(inverse)이 필요하다. 위의 식처럼 뷰변환 M은 이동(T)에 이은 회전(R), 즉 RT로 정의되고, 역변환은 다음과 같다. 회전 행렬의 역은 그 전치행렬과 같다.
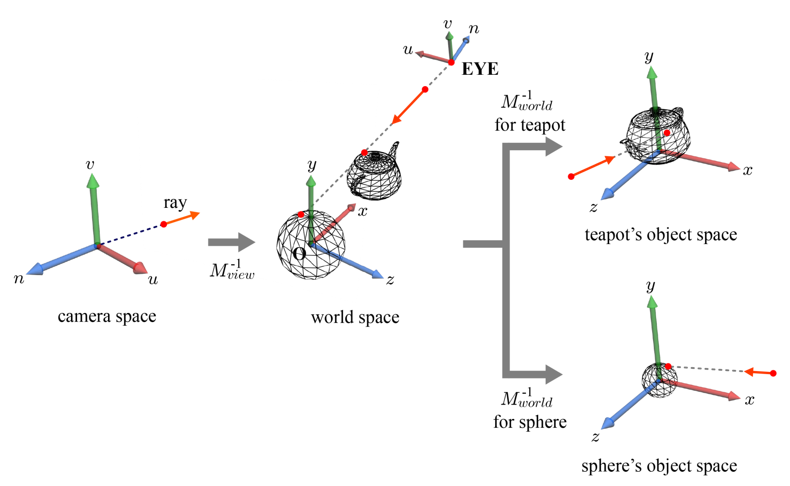
뷰 변환의 역을 이용해 카메라 공간 광선이 월드 공간으로 변환된다. 그 다음, 월드 공간 광선은 월드 변환의 역을 이용해 오브젝트 공간으로 변환된다.
위의 그림처럼 구와 주전자는 각자 고유의 오브젝트 공간과 월드 변환을 가지고 있음을 인지하고, 이러한 월드 변환의 역이 월드 공간 광선에 적용되므로, 구와 주전자는 각기 다른 오브젝트 공간 광선을 가지게 된다. 광선을 매개변수 방정식(parametric equation)으로 표현하면 다음과 같다.
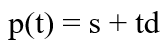
광선
여기서 s는 시작점을, d는 방향 벡터를 의미하는데, 매개변수 t는 [0, ∞] 범위에 있다.
2. Bounding Volume
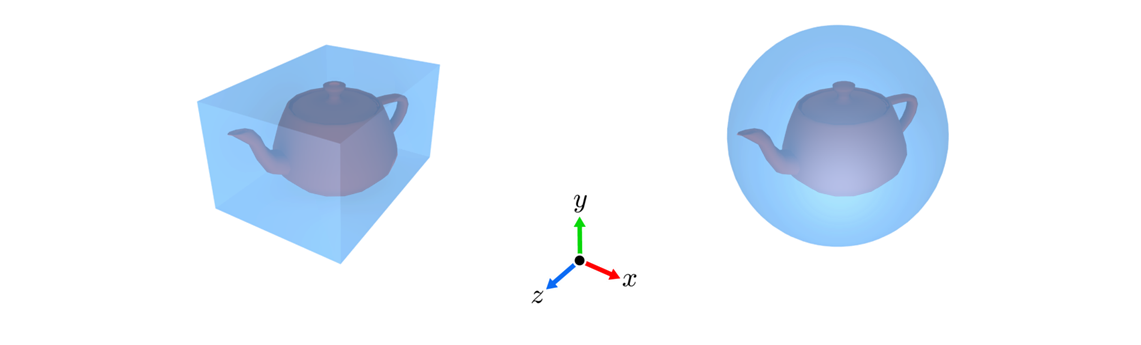
3D Bounding Volume
폴리곤 메시로 표현된 물체와 광선 간 교차 검사를 수행하기 위해서는 원칙적으로 물체의 모든 삼각형에 대해 광선-삼각형 교차 검사를 실시해야 한다. 하지만 이러한 교차 검사는 많은 시간이 필요로 해, 이보다는 부정확하지만 훨씬 빠른 방법인 바운딩 볼륨(bounding volume)을 구한 뒤 이를 광선과의 교차 검사에 사용한다.
하나는 좌표축과 나란한 직육면체로 AABB(axis-aligned bounding box)라 부르고 세 축별 범위로 정의되고, 다른 하나는 바운딩 구(bounding sphere)라고 부르며, 중심 좌표와 반지름 길이로 정의된다.
.
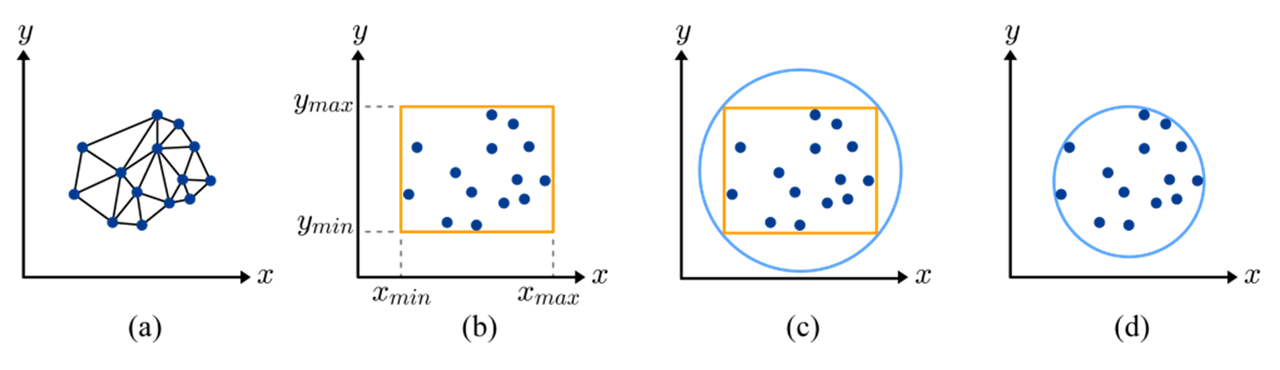
2D Bounding Volume
ABB 계산은 간단하다. 초기화를 위해 임의로 한 정점을 선택해 이 정점의 x좌표를 x_min,과 x_max에, 이 정점의 y좌표를 y_min과 y_max에 할당하며 나머지 정점을 하나씩 방문하여 min과 max값을 갱신한다. a에서 이를 통해 얻어진 2차원 AABB를 b에서 보여준다. 바운딩 구를 얻는 가장 단순한 방법은 AABB를 이용하는 것이다. 즉, AABB의 중점을 바운딩 구의 중심으로 취하고, AABB의 대각선 길이의 반을 바운딩 구의 반지름으로 취하면 된다. 하지만, 이렇게 얻어진 바운딩 구(c)는 종종 필요 이상으로 크다. (d)는 최적화된, 모든 정점들을 포함하는 '가장 작은' 바운딩 구를 보여준다. 바운딩 구를 사용한 결과는 폴리곤 메시 자체를 사용한 결과와 달라질 수 있다는 것을 명심하자.
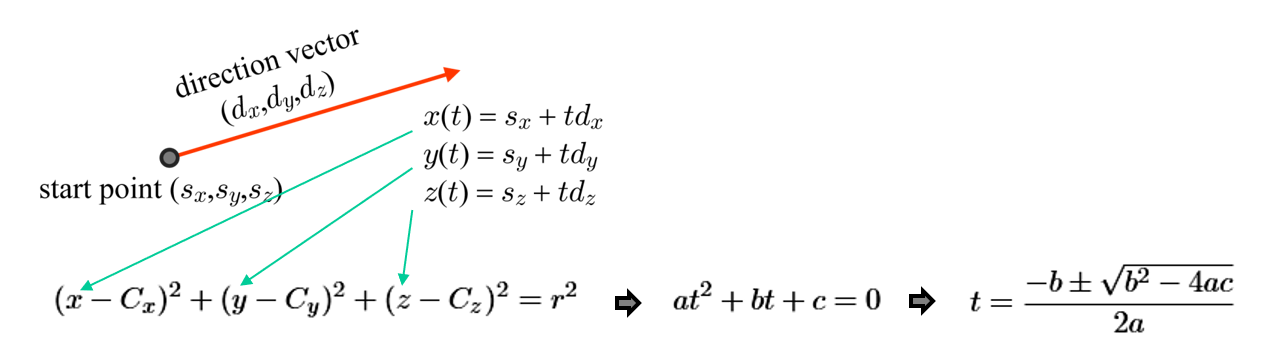
Bounding Volume Sphere와 ray의 교점을 구하는 풀이
3차원 광선은 다음과 같은 3개의 매개변수 방정식으로 정의된다. 구의 중심을 (C_x, C_y, C_z)로, 반지름을 r로 표기하고, t를 에 대해 풀기 위해 근의 공식을 쓰면 t를 구할 수 있다.
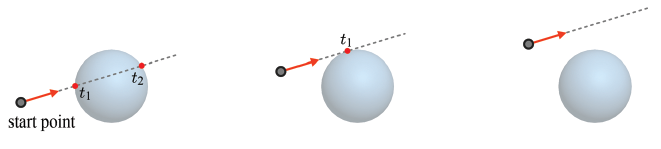
광선과 바운딩 구 사이의 교차점
판별식 b^2-4ac가 양수라면 서로 다른 두 실근을 얻게 되고, 판별식이 0이면 중근을 가지고, 만약 판별식이 음수라면 실근은 존재하지 않는다.
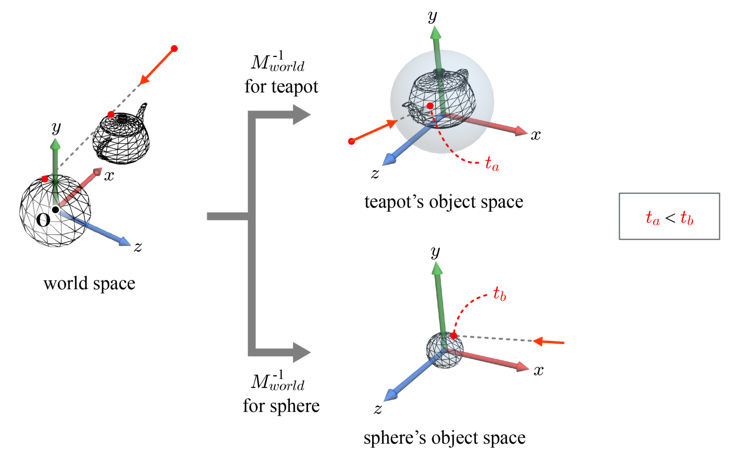
오브젝트 공간에서의 광선-물체 교차 검사
두 개의 바운딩 볼륨이 따로 처리되는데, 광선은 두 바운딩 볼륨과 모두 부딪힌다.
주전자의 바운딩 볼륨과 부딪히는 점에서의 매개변수 t_a가 구의 바운딩 볼륨과 교차하는 점에서의 매개변수 t_b보다 작다. 따라서, 주전자가 광선과 처음으로 교차하는(t가 더 작은) 물체가 더 먼저 부딪히게 된다.

그림 (a)는 Bounding Volume은 통과하지만 Object는 통과하지 않는다.
광선과 바운딩 볼륨 간 교차 검사는 종종 부정확한 결과를 산출한다. 광선이 바운딩 구와 교차하더라도 실제 폴리곤 메시와는 교차하지 않을 수 있다. 정확한 계산이 필요할 때에는 반드시 폴리곤 메시의 모든 삼각형과 광선 간 교차 검사를 수행해야 한다. 하지만, 만약 광선과 바운딩 볼륨이 교차하지 않는다면 폴리곤 메시는 광선과 교차하지 않는다고 보장할 수 있기 때문에 어느정도 수고를 덜 수 있다. 광선이 폴리곤 메시와 교차한다면 광선은 이 메시의 바운딩 볼륨과도 반드시 교차하므로, 필요한 광선-삼각형 교차 검사를 놓치게 되는 경우는 없다.
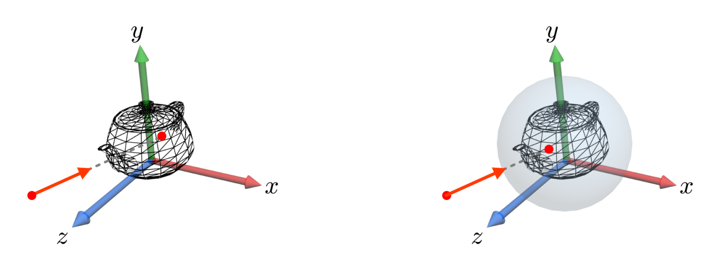
광선과 폴리곤 메시 간 교차 검사는 정확한 결과를 보장하지만 시간이 많이 소요된다. 바운딩 볼륨 간 속도는 빠르지만 부정확한 결과가 나올 수 있다.
확한 광선-물체 교차 검사를 위해서는 그 물체의 폴리곤 메시의 모든 삼각형과 광선 간 교차 검사를 수행해야 한다. 광선과 삼각형 <a, b, c>는 p점에서 교차하는데, 이 삼각형은 p에 의해 세 개의 작은 삼각형으로 나눠진다고 볼 수 있다. 삼각형 <p, b c>가 원래의 삼각형 <a, b, c>에서 차지하는 면적의 비중을 u라고 할 때, 이는 p가 a에 얼마만큼 가까이 있는지 말해준다.
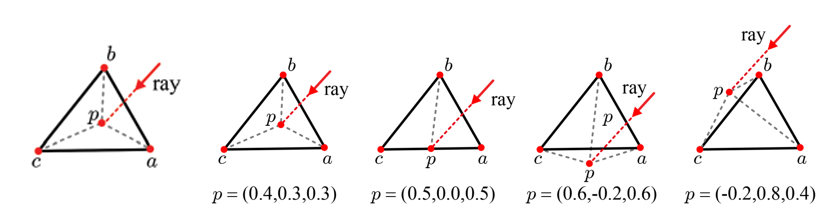
광선-삼각형 교차 검사
정확한 광선-물체 교차 검사를 위해서는 그 물체의 폴리곤 메시의 모든 삼각형과 광선 간 교차 검사를 수행해야 한다. 광선과 삼각형 <a, b, c>는 p점에서 교차하는데, 이 삼각형은 p에 의해 세 개의 작은 삼각형으로 나눠진다고 볼 수 있다. 삼각형 <p, b c>가 원래의 삼각형 <a, b, c>에서 차지하는 면적의 비중을 u라고 할 때, 이는 p가 a에 얼마만큼 가까이 있는지 말해준다.
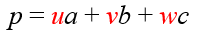
세 정점의 가중치 합
p는 다음과 같이 세 정점의 가중치 합으로 정의된다. 여기에서 (u, v, w)를 삼각형 <a, b, c>에 대한 p의 무게중심 좌표(barycentric coordinates)라고 부른다.
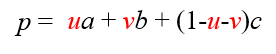
한편, u, v, w는 모두 [0, 1] 범위에 있으며 u + v + w = 1이 된다. 따라서 다음과 같이 다시 쓸 수 있다.
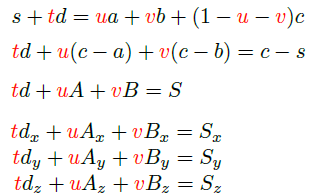
광선은 매개변수 방정식 s+td로 표현되고, 광선과 삼각형 <a, b, c> 간 교차점 계산은 다음과 같은 방정식을 푸는 것과 같다.
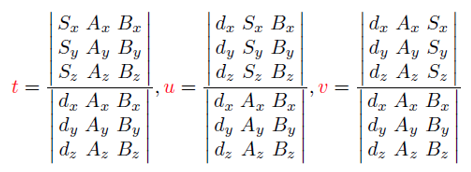
이는 크레이머 법칙(Cramer's rule)으로 풀 수 있다. 삼각형이 광선과 교차하는 점이 아니라, '삼각형이 놓인 무한한 넓이의 평면'이 광선과 교차하는 점'이다. 따라서, 교차점이 삼각형 안에 놓인다는 보장은 없다. 교차점이 삼각형 안에 있으려면, u>=0, v>=0, w>=0 조건을 만족해야 한다.
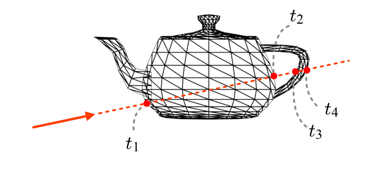
광선이 주전자와 여러 번 부딪힌다.
이 경우 가장 작은 양수 t를 가지는 교차점을 선택하면 된다.
3. Object Rotation and Arcball
지금까지는 화면을 클릭했을 때, 해당 좌표의 물체가 어떻게 적절하게 선택되는지 알아보았다. 이제는 그 물체를 드래그했을 때 회전하는 상호작용에 대해 알아보자. 우선, 아래 그림은 화면을 좌에서 우로 드래그했을 때 주전자가 돌아가는 것을 나타낸다. 그리고 화면에서 얻을 수 있는 정보는 오른쪽 그림같이 2D 화면상 pi에서 pi+1... pi+n 같이 연속적인 좌표를 얻을 수 있다.
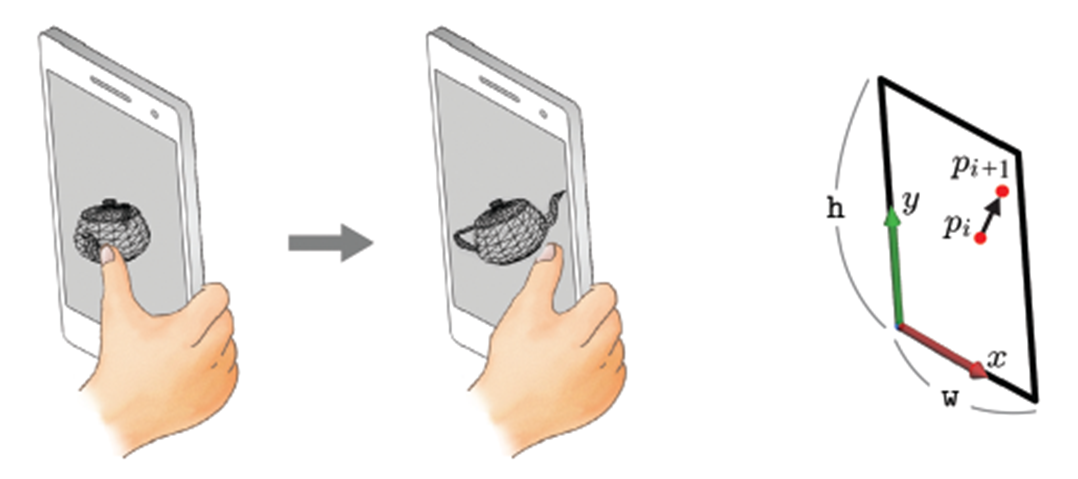
화면을 통한 Object rotation
여기서 Arcball이라는 개념이 등장한다. Arcball은 가상의 구로 X, Y 각 [-1,1] 범위의 정육면체 안에 존재하는데, 화살표 아래 x', y'를 나타내는 수식은 가로세로 각각 w, h인 스크린 좌표가 Arcball이 존재하는 정육면체에 어떻게 맵핑되는지를 나타낸다. 이때 Arcball 공간상에서 z 축으로는 +1인 지점에 맵핑이 된다.
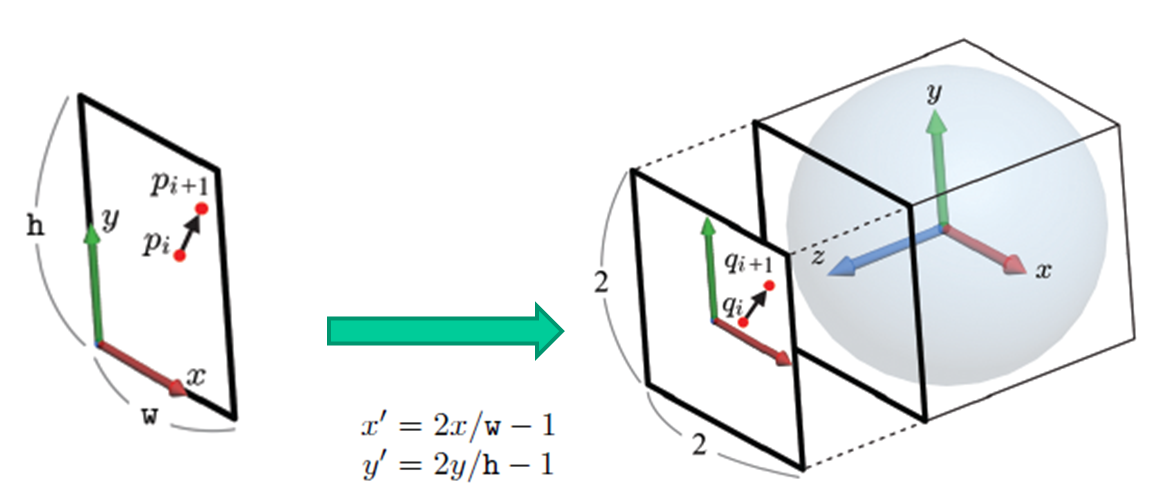
스크린 공간(좌) 에서 Arcball 공간상(우)으로 변환구의 방정식
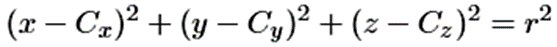
구의 방정식
이제 Arcball 공간상에 찍힌 좌표를 통해 Arcball의 표면에 projection을 시킨다. z좌표만 모르기 때문에 구의 방정식에 x, y를 대입해서 풀어낼 수 있다. 아래 그림처럼 알아낸 Arcball의 표면 연속된 좌표 v_i와 v_i+1 두 점의 좌표를 외적 하여 rotation axis 또한 구해낼 수 있다. 또한 단위 구 위의 점이므로 두 점 모두 단위 벡터이다. 따라서 내적을 통해서 두 점 사이의 각도 또한 쉽게 알 수 있다. 또한 오른쪽 그림처럼 Arcball 표면상에 projection 시킬 수 없는 경우는 z좌표를 0으로 하는 xy-plane상에 가장 가까운 Arcball의 표면에 그 아래 수식을 이용해 위치시킨다.
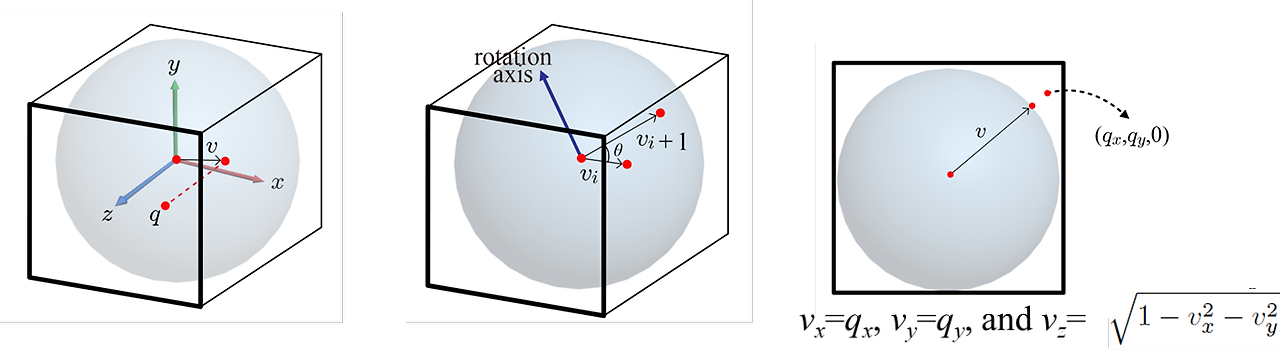
구 표면으로 projection(왼쪽)과 외적을 통한 rotation axis 표현(가운데) 그리고 예외 처리(오른쪽)
이렇게 Arcball을 이용해 회전축과 각도 모두 구할 수 있다는 것을 알았다. 하지만 정작 회전해야 할 object가 아직 언급이 없는데, 그래픽스에서는 Arcball에서 구한 회전축을 camera 공간상에 위치시키는 방법을 사용한다. 이렇게 위치시킨 회전축 또한 역변환을 통해 object space로 변환하여 object space상 변환된 회전축을 기준으로 구한 각도만큼 회전을 시키는 것이다. 이렇게 2D 화면상 pi에서 pi+1... pi+n를 연속되게 계산하면 화면을 드래그했을 때, 물체의 회전을 만들 수 있게 되는 것이다. (회전축과 각도가 있으면 회전 변환이 가능하다는 것은 Quaternion 참고)
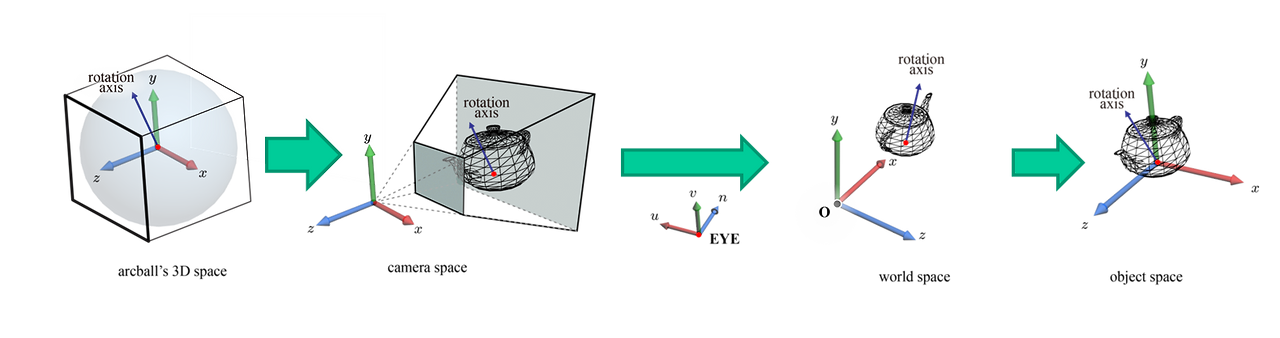
Arcball 공간을 object space로 변환
이렇게 화면에 해당 Object가 어떻게 선택되는지 또 드래그했을 때 어떻게 회전하게 될 수 있는지를 파악할 수 있다.
'Computer Graphics > Graphics Theory' 카테고리의 다른 글
| Computer Graphics [5] : 카메라 시점 (Camera View) (0) | 2025.02.02 |
|---|---|
| Computer Graphics [4]: 셰이더 (Shader) (1) | 2025.01.11 |
| Computer Graphics [3]: 텍스쳐 (Texture) (1) | 2025.01.11 |
| Graphics Theory [7] : 렌더링 파이프라인 (Rendering Pipeline) (0) | 2024.10.08 |
| Computer Graphics [2]: 변환 (Transformation) (2) | 2024.09.18 |