
컴퓨터 비전에서는 이미지 정보와 처리의 원리를 잘 이해하는 것이 중요하다. 이미지 처리는 객체 인식, 추적, 분할 및 분석과 같은 컴퓨터 비전의 핵심 기술을 지원하며 효과적인 노이즈 제거, 화질 개선 및 이미지 변환 기술을 통해 실제 환경에서 얻은 데이터를 보다 신뢰할 수 있는 형태로 변환하여 정확한 결과를 도출할 수 있다. 그리고 이미지의 기하학적 특성을 이해하면 왜곡을 보정하고 다양한 시점에서의 3D 재구성을 가능하게 하여 더욱 현실적인 분석과 응용을 지원한다. 이러한 원리는 머신 러닝 및 딥 러닝 알고리즘과 결합되어, 이미지 기반 데이터의 처리 및 분석에 필수적인 기초 지식을 제공한다. 따라서 이미지 처리 원리에 대한 깊은 이해는 컴퓨터 비전 시스템의 개발 및 최적화에 있어 필수적이다.
1. Camera, Geometry and Photometry
Digital Image Information
우리가 보고 있는 세계는 연속적인 세계이며 3차원의 공간이다. 이를 카메라로 찍으면 우리가 보는 세상은 2차원의 이미지로 Projection된다. 이렇게 3D to 2D projection이 일어나는 과정에서 연속적인 세계가 디지털로 바뀌면서 불연속적인 수치로 바뀌고 각 픽셀은 어떤 특정한 하나의 점을 점유하는 것이 아니라, 어떤 영역의 평균을 계산한 값이 된다. 또한 Capacitor의 용량 문제로 인해 밝기 제한 값 자체의 표현 범위가 0-255로 줄어든다.

세상을 이미지에 본 뜨기 위해서는 어떻게 해야할까? 먼저 물체 앞에 필름을 놓는 것이다. 물체를 필름에 인화한다는 것은 물체의 한 점이 필름의 한 점에 닿게 하는 일과 같다. 그러나, 실제로는 아래 왼쪽의 그림과 같이 물체의 한 점은 필름의 모든 면에 닿게 된다. 이를 해결하기 위해 Pinhole Camera의 개념이 도입되었다. 필름과 물체 사이에 대부분의 빛을 차단하기 위해 배리어를 두는 것이다. 배리어는 일종의 조리개와 같다. 이는 Blur를 줄여주며 물체의 한 점이 필름의 한 점에 닿게 하는 것을 가능케한다. 하지만 이러한 방법은 필름에 도달하는 빛의 양이 매우 적어 어둡다는 문제가 생긴다.


렌즈를 구멍에 부착하면 빛을 한 곳에 모아 쏠 수 있으며 이는 카메라의 초점 정보를 활용하여 거리 정보를 담는 역할을 한다. 카메라의 초점 거리(f)와 중앙점(c)은 빛의 경로를 조절하여 이미지의 선명도를 높이고 원하는 대상을 명확히 포착할 수 있게 해준다. 이를 통해 카메라는 물체와의 거리 정보를 효과적으로 기록할 수 있다.

Projective Geometry
카메라로 사진을 찍는 것은 3D 이미지를 2D로 투영하는 과정으로 볼 수 있다. 이 과정에서 직선은 여전히 보존되지만, 거리 정보와 각도 정보는 잃게 된다. 즉, 3D 공간의 객체는 2D 평면에 표현되면서 서로 간의 거리와 각도가 왜곡되며 실제 모습과는 다른 형태로 나타날 수 있다. 이로 인해 시각적 정보는 제한되지만, 기본적인 형태와 직선은 여전히 인식할 수 있는 상태로 유지된다.



Vanishing points and lines
기차의 철로를 생각해보자. 기차 철로는 실제로는 평행한 두 개의 직선으로 이루어져 있지만, 멀리서 보면 두 선이 점점 가까워져서 결국엔 한 점에서 만나는 것처럼 보인다. 그 한 점이 바로 소실점(vanishing point)이다. 이번에는 평행한 직선들의 각도를 조금씩 틀어보는 상황을 상상해자. 예를 들어, 도시의 거리를 보면 길거리에는 수많은 건물, 전봇대, 도로 등이 있는데, 이들은 모두 평행하게 정렬되어 있지 않고, 각각의 각도를 가지고 있다.
각기 다른 방향의 평행한 직선들은 각기 다른 소실점을 가지게 되며, 이 소실점들이 무수히 많아질 수 있다. 이 소실점들이 특정한 패턴으로 정렬되면, 그들을 연결하는 가상의 선이 생기는데 이 선을 소실선(vanishing line)이라고 한다. 지평선이 이런 소실선의 대표적인 예로 멀리서 보면 평행한 직선들이 수평선(지평선)으로 향하며, 그 뒤쪽의 정보는 더 이상 인식되지 않는다.


컴퓨터 비젼은 2D Image로부터 3D를 reconstruction하는 것이라고 볼 수 있다. 이처럼 3D를 2D로 프로젝션해도 보존되는 이러한 평행 선의 원근법과 기하학적 정보를 활용하여 이미지에서 3차원 구조를 복원할 수 있을 것이다. 여러 소실점을 찾으면 서로 다른 평면들의 방향을 추정할 수 있으며, 이를 통해 3D 좌표를 복원하는 것이다. 카메라 파라미터와 소실점 간의 관계를 분석해 깊이 정보까지 추정할 수 있으며, 직선 감지 알고리즘을 통해 평면의 각도와 3D 구조를 재구성하는 것이 가능해진다.
평행선의 원근법을 활용하여 3차원 구조를 복원하는 과정은 여러 단계로 이루어진다. 기본적으로 2D 이미지에서 평행선과 소실점을 찾는 것은 3D 공간의 기하학적 정보를 추론하는 데 중요한 역할을 한다. 예를 들어, 도로의 양쪽에 있는 가로수를 촬영한 이미지를 생각해보겠습니다. 이 경우, 가로수가 카메라에 가까운 부분은 크고 멀어질수록 작아지는 원근감을 나타내며 이는 두 개의 평행선(가로수의 줄)과 하나의 소실점(가로수가 멀어지는 지점)을 형성한다. 여러 개의 소실점을 찾으면, 각각의 소실점이 서로 다른 평면의 방향을 나타내며, 이를 통해 다양한 평면의 기하학적 구조를 추정할 수 있다. 예를 들어, 소실점 A는 도로의 방향을, 소실점 B는 가로수의 방향을 나타낼 수 있다.
이런 방식으로, 소실점 간의 관계를 분석하면 카메라의 위치와 관점에 따라 각 평면의 경사도와 방향을 파악할 수 있다. 이러한 정보를 바탕으로 카메라의 파라미터(예: 초점 거리, 센서 크기)와 소실점의 관계를 활용해 깊이 정보를 추정할 수 있는데 직선 감지 알고리즘을 사용하여 이미지 내의 직선을 식별하고 이들이 생성하는 평면의 각도를 측정함으로써 각 평면의 3D 구조를 재구성할 수 있다. 결과적으로, 이러한 과정을 통해 원근법과 기하학적 정보를 결합하여 2D 이미지에서 3D 좌표를 복원할 수 있는 가능성을 제공하며 이는 로봇 비전, 자율주행차 및 다양한 컴퓨터 비전 응용 프로그램에서 중요한 역할을 한다.
요약 : 사진 촬영은 3D를 2D로 투영하는 과정으로 직선은 보존되지만 거리와 각도 정보는 손실된다. 소실점과 소실선을 활용하면 2D 이미지로부터 3D 구조를 복원할 수 있다.
Image Geometry

세계 좌표계에서 관심 있는 객체(Object of Interest)는 (U, V, W) 좌표로 표현된다. 여기서 U, V, W는 각각 객체의 위치를 나타내는 축으로 U는 수평 축, V는 수직 축, W는 깊이를 나타낸다. 이를 통해 현실 세계에서 객체의 물리적 위치와 방향을 정의하며, 3D 공간에서 다른 객체와의 관계를 이해할 수 있다.

카메라 좌표계는 (X, Y, Z)로 구성되며 여기서 Z축은 광축(optic axis)을 나타낸다. 주어진 그림은 광축을 따라 초점 거리(f) 밖에 위치한 이미지 평면을 보여준다. 초점 거리 f는 카메라 렌즈의 특성을 정의하며, 3D 공간에서 물체의 위치를 2D 이미지로 변환하는 데 중요하다. 3D에서 3D로의 변환을 수행할 때는 주로 평행 이동(translation)과 회전(rotation)만이 변하게 되며, 이는 물체의 상대적 위치와 방향을 유지하면서 카메라의 시점에 따라 표현 방식을 조정할 수 있게 해준다. 이러한 변환을 통해 객체의 모습은 카메라의 위치와 방향에 따라 달라지지만, 그 내부의 공간적 관계는 보존된다.
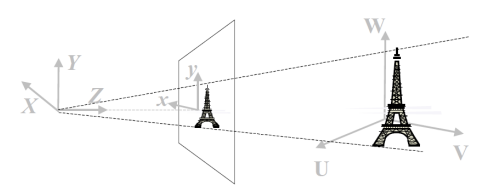
전방 투영(Forward Projection)은 3D 공간의 좌표 (X, Y, Z)를 2D 이미지 평면의 좌표 (x, y)로 변환하는 과정이다. 이 과정은 현실 세계의 3D 객체를 이미지 평면에 투영하는 것으로, 물체의 위치와 형태를 2D 형태로 표현한다. Z 방향에 있는 모든 점은 이미지 내 하나의 픽셀에 집약되며, 이는 깊이 정보가 소실된다는 것을 의미한다. 따라서 다양한 깊이에 있는 객체들이 동일한 2D 평면 상의 위치에 투영되어 시각적으로 구분되지 않을 수 있다. 이러한 투영 과정을 통해 우리는 3D 세계를 2D로 이해할 수 있지만, 깊이 정보를 잃게 되는 것이다.
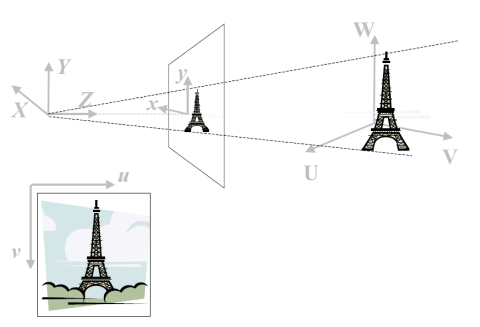
이미지는 픽셀 좌표(u, v)로 변환되어 디지털화된다. 이 과정에서 각 픽셀은 이미지의 특정 위치에 해당하는 고유한 좌표를 가지며, 이로 인해 아날로그 신호가 디지털 데이터로 변환된다. 픽셀 좌표는 이미지의 해상도와 관계가 있으며, 더 높은 해상도는 더 많은 픽셀을 포함해 더 세밀한 디테일을 표현할 수 있게 해준다.
요약 : 이처럼 카메라로 사진을 찍는 과정은 3D 세계 좌표를 2D 픽셀 좌표로 변환하는 것이며 컴퓨터 비전의 3D reconstruction은 이 과정을 역으로 수행하여 2D 이미지에서 물체의 3차원 형상, 실루엣, 색상 등의 정보를 복원하는 것을 목표로 한다. 이를 위해 이미지에서 특징을 추출하고 카메라 보정을 통해 물체의 3D 위치를 계산하며 이를 바탕으로 3D 모델을 생성하고 색상을 매핑하여 현실 세계의 물체를 재구성한다.
Image Photometry
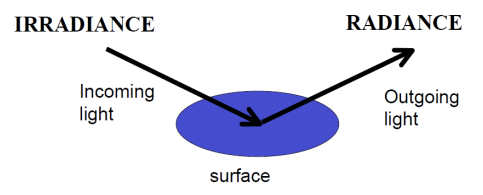
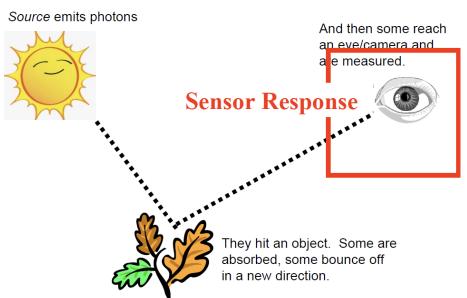
Irradiance는 단위 면적당 표면에 도달하는 빛의 양을 측정하며, radiance는 단위 면적과 특정 방향으로 방출되거나 반사되는 빛의 양을 나타낸다. Irradiance는 빛의 에너지가 표면에 얼마나 도달하는지, radiance는 표면에서 나가는 빛이 특정 방향으로 얼마나 방출되는지를 측정하는 개념이다. 센서(카메라, 눈 등)가 감지하는 것은, 광자가 물체에 부딪힌 뒤 센서에 닿는 시점이다.
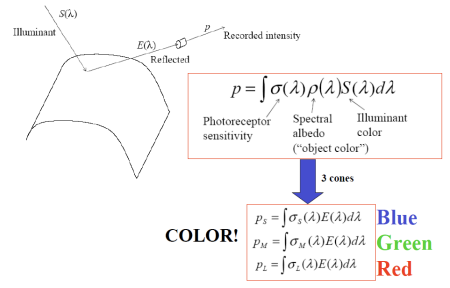
p: 물체가 반사한 빛이 카메라 센서에 도달해 기록된 값이다. 카메라에서 측정하는 최종적인 이미지 정보를 의미하며, 물체의 색, 조명 조건, 센서의 감도 등 여러 요인에 의해 영향을 받는다.
Photoreceptor Sensitivity: 카메라의 센서가 빛을 얼마나 잘 감지할 수 있는지를 나타내며 센서가 빛의 다른 파장대나 밝기 변화를 얼마나 민감하게 인식할 수 있는지를 결정하는 요소이다. 감도가 높으면 약한 빛도 잘 감지할 수 있지만, 노이즈도 함께 증가할 수 있다.
Spectral Albedo (Object Color): 물체가 다양한 파장의 빛을 얼마나 반사하는지를 나타내며, 이는 우리가 인식하는 물체의 색에 해당한다. 물체는 들어오는 빛 중 일부 파장을 흡수하고 일부를 반사하기 때문에, 그 반사되는 빛의 스펙트럼에 따라 물체의 색이 결정된다.
Illuminant Color: 물체에 도달하는 빛의 색 또는 스펙트럼 분포를 의미한다. 조명은 물체가 반사하는 빛의 양과 색에 직접적인 영향을 미치며, 들어오는 빛의 스펙트럼에 따라 물체가 어떻게 보이는지가 달라진다. 예를 들어, 태양광과 인공조명은 각각 다른 색을 가진 빛을 제공하며, 이는 물체의 색에 영향을 준다.
요약 : 카메라는 물체와 필름 사이에 barrier와 렌즈를 통해 빛을 모아 이미지를 형성하며, 촬영 과정은 World Coordinate에서 Camera Coordinate, Image Coordinate, 그리고 Pixel Coordinate로 변환된다. 세상을 이미지화함으로써 연속적인 값이 디지털화되어 밝기의 범위는 0-255로 제한되고, 한 픽셀은 특정 점이 아닌 영역의 평균 값을 나타낸다. 또한 사진 촬영 과정에서는 3D 세계가 2D 이미지로 투영되면서 길이와 각도 정보는 손실되지만, 직선은 여전히 보존된다. 이 직선의 소실점정보를 통해 2D의 정보로 3D를 재구성할 수 있다.
2. Intensity Surfaces, Gradients and Linear Operators
Visualizing Images
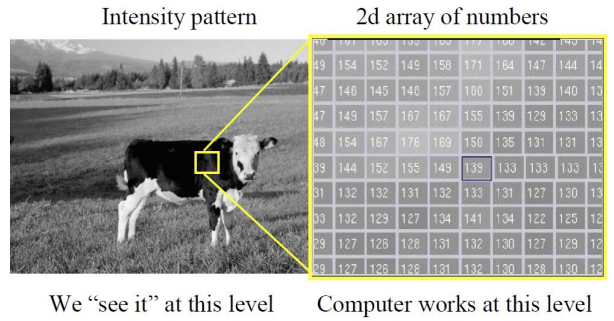
왼쪽 같이 실제 이미지는 연속적인 색상과 밝기 정보를 제공하지만, 컴퓨터는 이를 2D 배열 형태로 디지털화하여 각 픽셀이 특정 영역의 평균 값을 나타내도록 변환한다. 이 과정에서 3D에서 2D로의 프로젝션으로 인해 세부 정보와 깊이 정보는 손실되며, 픽셀 하나하나가 포함할 수 있는 영역이 커지게 된다.
Images as Surfaces
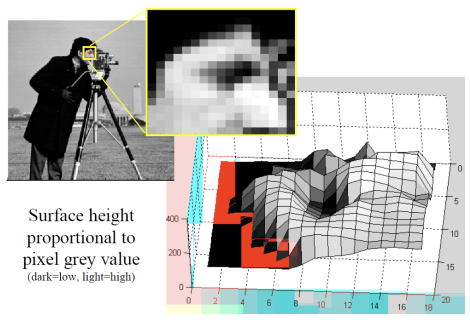
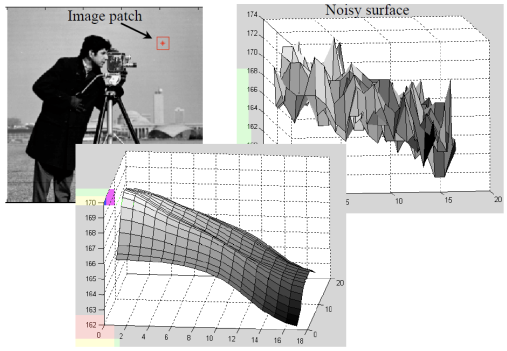
2차원 이미지의 밝기 정보를 3차원으로 변환하면, 각 픽셀의 밝기를 해당 위치의 높이로 해석하여 3차원 표면을 생성할 수 있다. 이 과정에서 밝기가 높은 픽셀은 높은 구조물처럼, 밝기가 낮은 픽셀은 낮은 구조물처럼 표현되어, 이미지의 밝기 패턴을 3차원 형상으로 시각화하고 분석할 수 있다.
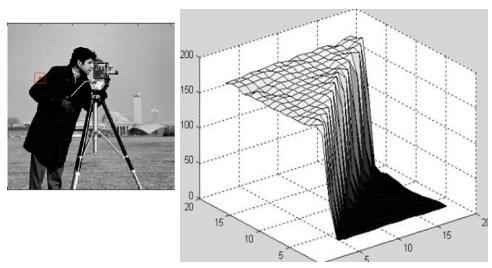
왼쪽 같이 이미지의 배경을 3차원 형상으로 표현하면 높이값이 거의 일정하지만 들쑥날쑥한(high-frequency) 표면이 되고, 객체의 엣지를 표현하면 높이값의 차이가 커서 언덕처럼 보인다. 이 방법을 통해 밝기값이 큰 부분은 중요한 객체의 단서가 될 수 있다. 밝기 정보를 높이로 보고, 밝기 언덕을 오르락내리락하는 개념으로 생각하면, gradient 벡터를 사용하여 밝기값의 큰 차이를 감지할 수 있다. gradient 벡터는 이미지의 각 지점에서 밝기 변화의 방향과 크기를 나타내며, 밝기값이 빠르게 변하는 지점을 식별하는 데 유용하다. 이를 통해 이미지 내에서 객체의 경계나 중요한 특징을 효과적으로 찾아낼 수 있다.
Math Example: 1D Gradient
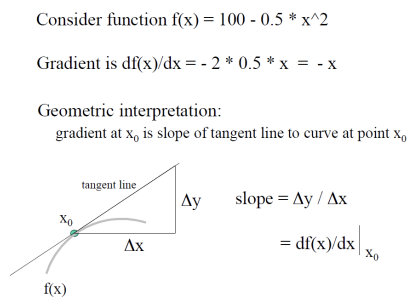
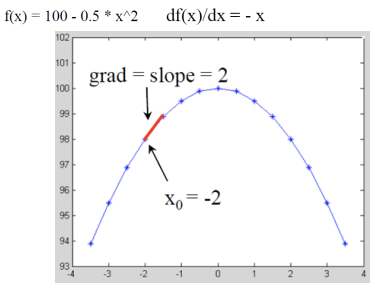
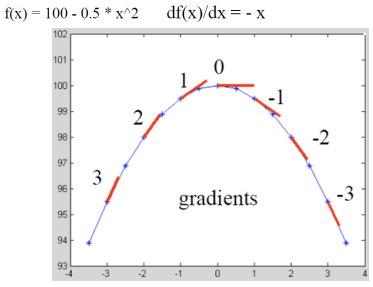
실제 세계의 연속적인 밝기 변화율을 분석하기 위해 그래디언트를 사용할 수 있지만 이미지 데이터는 이산적(discrete) 형태로 존재하기 때문에 이를 직접적으로 적용할 수 없다. 이 경우 이미지의 각 픽셀을 통해 평균적인 변화율을 계산하여 연속적인 정보를 근사하는 방법을 사용할 수 있다. 예를 들어, 한 픽셀의 밝기 값과 그 이웃 픽셀들의 밝기 값을 비교하여 변화율을 추정함으로써 주변 픽셀에서의 밝기 변화 패턴을 파악할 수 있다. 즉 이웃 픽셀 간의 밝기 차이를 계산하여 그래디언트를 근사하는 것이다.
Math Example: 2D Gradient
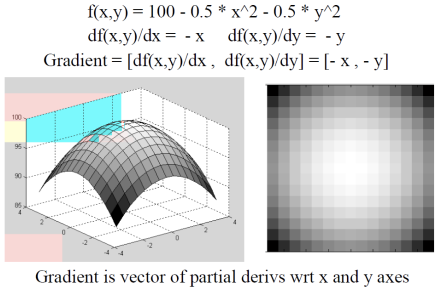
2차원 이미지에서 gradient는 각 픽셀의 x 방향과 y 방향의 밝기 변화율을 나타내는 벡터이며 각각의 원소는 x방향, y방향에 대해 편미분한 값이다. 이를 통해 각 픽셀에서의 gradient를 계산할 수 있으며, 경사가 큰 영역은 밝기 변화가 급격하여 중요한 특징이나 경계를 의미할 수 있다. 그라데이션 같아 보이는 우측 이미지에서 보듯이, 각 픽셀의 방향별 gradient를 구하여 경사가 큰 부분을 식별함해 유의미하게 다룸으로써 중요한 정보나 객체의 경계를 효과적으로 분석할 수 있다

화살표의 크기는 gradient의 크기다.큰 화살표에서 작은 화살표 방향으로(gradient가 큰 방향에서 gradient가 작은 방향으로) 모인다. 밝기 정보가 높은 곳으로 모인다.
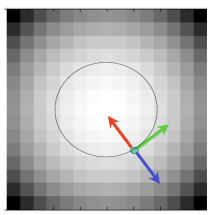
- [Red] Vector g points uphill (경사도가 높은 방향) : 이 벡터는 이미지에서 밝기가 가장 급격하게 증가하는 방향을 나타낸다. 즉, 밝기 변화가 가장 크고, 이 방향으로 올라가면 높이가 가장 빨리 증가한다. 이러한 벡터는 고지대나 경사가 급한 부분을 가리킨다.
- [Blue] Vector -g points downhill (경사도가 낮은 방향) : 이 벡터는 경사가 낮은 방향을 나타내며, gradient 벡터의 반대 방향이다. 즉, 밝기가 가장 급격히 감소하는 방향을 나타내며, 이 방향으로 이동하면 높이가 가장 빨리 감소한다.
- [Green] Vector [g'y, g'x] is perpendicular (수평 방향의 벡터) : 이 벡터는 gradient 벡터와 수직이며, 일정한 높이(또는 밝기)를 유지하는 방향을 나타낸다. 즉, gradient 벡터와의 접선 방향을 의미하며, 같은 높이에서 이동할 때의 방향을 보여준다. 이 벡터는 경사면에서 수평선을 따라 움직이는 방향을 나타내며, 경사면의 평탄한 부분을 따라 움직일 때의 경로를 가리킨다.
Gradient는 함수의 변화율을 나타내는 벡터로, 특히 다변수 함수의 경우 각 변수에 대한 편미분으로 구성된다. 예를 들어, 2차원 공간에서 함수f(x, y) = x^2 + y^2의 그래디언트를 계산하면, ∇f=(∂f/∂x,∂f/∂y)=(2x,2y)가 된다. 이 그래디언트는 각 점에서의 함수의 최댓값 방향을 나타내며 예를 들어 점 (1, 1)에서의 그래디언트는 (2, 2)로 이는 이 점에서 함수 값이 증가하는 방향이 (2, 2)임을 의미한다. 따라서 그래디언트는 최적화 문제에서 경사 하강법과 같은 알고리즘에서 중요한 역할을 한다.
편미분은 다변수 함수에서 특정 변수에 대한 미분을 구하는 방법으로 다른 변수는 상수로 간주한다. 예를 들어, 함수 f(x, y) = x^2y + 3xy^2를 고려해보면 이 함수에 대한 에 대한 편미분은 를 상수로 간주하고 에 대해서만 미분한 결과를 구하면 된다. 반면, y에 대한 편미분을 구하면 반대로 적용하면 된다. 이렇게 각 변수에 대한 편미분을 구함으로써 다변수 함수의 각 변수의 변화가 함수에 미치는 영향을 분석할 수 있으며, 이는 그래디언트 계산의 기초가 되고 특정 점에서의 최적화 방향을 제시합니다.
이미지 픽셀 밝기값의 그라디언트를 계산하여 변화량을 측정함으로써 경계나 엣지를 감지할 수 있다. 이미지를 로 나타내면 ∇I=(∂I/∂x,∂I/∂y)로 표현되는 그래디언트는 각 픽셀의 x방향과 y방향에서의 밝기 변화율을 제공한다. 이 정보는 이미지에서 밝기 변화가 큰 영역, 즉 객체의 경계선이나 형태를 강조하여 추출하는 데 사용되는 것이다. 예를 들어, Sobel 필터와 같은 엣지 감지 알고리즘은 그래디언트를 이용하여 밝기 변화가 급격한 부분을 찾아내어 이미지를 더 명확하게 분석할 수 있게 도와준다. 이러한 방식으로 Gradient는 이미지의 구조를 이해하고, 다양한 컴퓨터 비전 응용에 필수적인 역할을 하기에 반드시 이해해야 한다.
Numerical Derivatives
이미지의 픽셀 값은 이산적이기 때문에 연속 함수에서의 미분 개념을 적용할 수 없어 테일러 급수를 사용해 국소적인 근사로 기울기를 계산한다. Gradient(기울기)는 다변수 함수에서 각 변수에 대한 편미분의 모음으로 테일러 급수를 통해 유도할 수 있다. 먼저 현재 픽셀과 오른쪽에 있는 픽셀을 가지고 gradient를 구해보자.
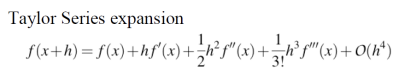
given f(x), O(h^4)는 error를 의미한다. 계산하지 않은 텀에 대해서는 전부 에러로 처리하므로, 어디까지 구하는지는 각자의 선택에 달렸다.
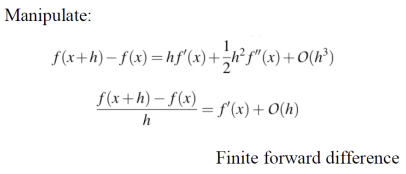
현재 픽셀과 오른쪽 픽셀을 가지고 gradient를 구하면, 에러가 O(h)로 나온다. 현재 픽셀과 오른쪽 픽셀을 가지고 구한 미분값을 Fininte Forward Diference라고 한다. 이젠 현재 픽셀과 왼쪽 픽셀의 gradient를 구해보겠다.
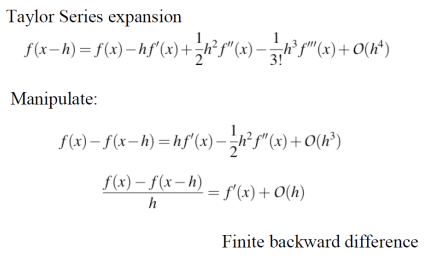
현재 픽셀과 왼쪽 픽셀을 이용해 gradient를 구하는 방법은 Finite Backward Difference라 한다. Forward Difference가 현재 픽셀과 오른쪽 픽셀 간의 밝기 차이를 이용했다면, Backward Difference는 현재 픽셀과 왼쪽 픽셀의 차이로 기울기를 계산한다. 이 방법으로도 기울기를 구할 수 있지만, 오차는 역시 O(h) 수준이다. Forward와 Backward Difference는 각각 한 방향에서만 근사하기 때문에 오차가 발생하는데, 이 두 값을 평균하여 Central Difference를 사용하면 오차를 O(h²)로 줄일 수 있어 더 정확한 기울기 계산이 가능하다.

위의 이미지를 보면, f(x+h)-f(x-h)를 수행하면, 수식적으로 h^2 텀이 사라지는 것을 볼 수 있다. 따라서 결국에 남게 되는 에러가 O(h^2)이다. 위의 finite forward difference와 finite backward difference의 에러에 비해 한 텀이 사라져서 에러가 원래 수식보다 줄어든 것을 알 수 있다. 왼쪽 픽셀과 오른쪽 픽셀을 가지고 구한 미분값을 Finite Central Difference라고 한다. 최종적으로, finite forward difference와 finite backward difference보다 finite central difference가 좀 더 정확한 것을 알 수 있다.
O(h)와 O(h²)는 계산된 값의 오차 정도를 나타내는 표기법으로, 여기서 h는 두 픽셀 간의 거리 또는 미세한 변화량을 의미한다.
- O(h)는 오차가 변화량 h에 비례해 발생한다는 뜻이다. 즉, h가 작아질수록 오차도 작아지지만, 상대적으로 천천히 줄어든다. 예를 들어, Forward Difference와 Backward Difference는 오차가 O(h)이므로, 이 방법들은 h가 절반이 될 때 오차도 절반으로 줄어든다.
- O(h²)는 오차가 h의 제곱에 비례하여 발생함을 의미한다. h가 작아질수록 오차가 훨씬 빠르게 줄어드는데, 예를 들어 Central Difference의 경우 h가 절반으로 줄면 오차는 1/4로 감소한다. 따라서 O(h²) 방식은 동일한 h 값에서 O(h) 방식보다 더 정확한 근사값을 제공한다.
위 과정을 통해 단변수 함수의 미분값을 구했다면, 다변수 함수의 경우 각각의 변수에 대해 편미분을 계산하여 Gradient를 구한다. 각 변수에 대해 같은 방식으로 Forward Difference 또는 Central Difference를 사용하여 편미분을 계산한 후, 이를 종합하면 해당 점에서의 Gradient 벡터를 얻을 수 있다.

우측 상단 gradient image는 x방향으로 구한 gradient이다. 자세히 보면, 수평 방향으로 경계가 좀 더 뚜렷한 것을 확인할 수 있다. 우측 하단 gradient image는 y방향으로 구한 gradient이다. x방향으로 구한 gradient와는 반대로, 수직 방향으로 경계가 뚜렷한 것을 확인할 수 있다.
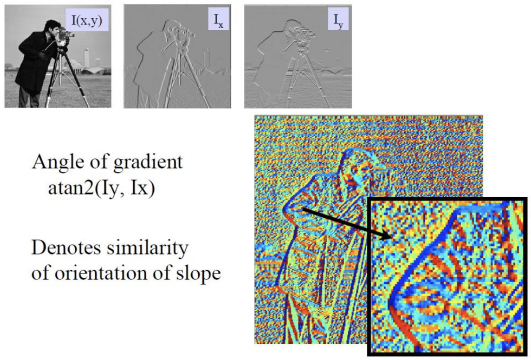
알록달록한 우측 하단 이미지는 similarity of orientation of slope 를 나타낸 것이다. 색상은 방향(orientation)을 나타내고, 색의 강도나 밝기는 기울기의 크기를 표현된다. 이미지에서 gradient(기울기)는 픽셀 간의 값의 변화를 나타내며, 그 방향은 orientation(방향성)으로 표시된다. Gradient가 큰 영역은 픽셀 값의 변화가 급격한 부분으로, 이는 이미지에서 객체가 나누어지는 중요한 경계를 나타낼 수 있다. 예를 들어, 이미지의 팔 부분에서 gradient의 방향이 일정한 구간은 동일한 orientation을 가지며 파란색으로 표시된다. 이는 이 구간이 유사한 경향을 따른다는 것을 의미한다.
반면에, 다른 영역은 여러 방향으로 gradient가 작거나 불규칙하게 발생하여, 마치 노이즈처럼 보인다. 이때 gradient가 작더라도 그 방향, 즉 orientation은 여전히 존재하며, 그 값들이 서로 다르기 때문에 혼란스럽게 보이는 것이다. 결과적으로, gradient가 큰 부분은 객체 간의 경계를 나타내며, 비슷한 pixel의 연속이라면(gradient가 작다면), 이것은 동일한 객체 내의 픽셀임을 알 수 있다.
다음과 같이 모든 픽셀 기준 왼쪽 픽셀과 오른쪽 픽셀의 gradient를 구해보자
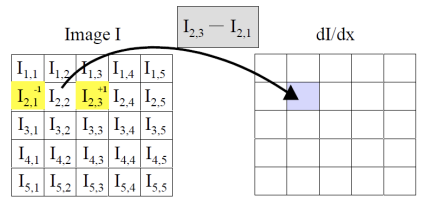
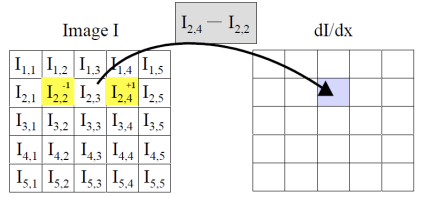
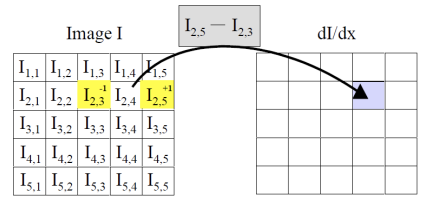
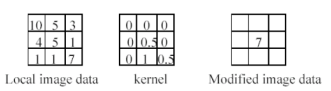
선형 필터링에서 컨볼루션 커널 (혹은 필터 마스크)은 이미지의 각 픽셀과 이웃한 픽셀에 적용되는 작은 행렬(가중치 배열)이다. 이 행렬을 사용하여 각 픽셀 주변의 이웃 픽셀들을 가중합한 결과를 얻고, 이를 통해 새로운 이미지를 생성한다. 가중치들은 각각의 이웃 픽셀이 현재 픽셀의 최종 값에 얼마나 기여하는지를 결정한다. 여기서 선형이라는 의미는 픽셀 값들이 단순히 커널의 가중치에 따라 스케일링되고 더해지는 연산이라는 것이다. 커널의 크기와 값에 따라 다양한 효과를 낼 수 있는데, 예를 들어 평균값 커널은 이미지를 부드럽게 만들고, 미분 커널은 경계나 에지를 강조하는 역할을 한다.
- general process : origin 픽셀에 weighted sum한 결과로 새로운 이미지를 생성한다
- properties : linear filter의 결과는 input의 선형 함수이다.
위와 같은 linear combination을 모든 픽셀에 대해 진행할 것이다. 컨볼루션은 이미지 f에 필터(혹은 커널) h를 적용해 새로운 이미지를 생성하는 연산 방법인데, 이 과정 이미지 f에 kernel h를 통과시키는 수식(위의 linear combination 과정)을 convolution으로 표현할 수 있다.
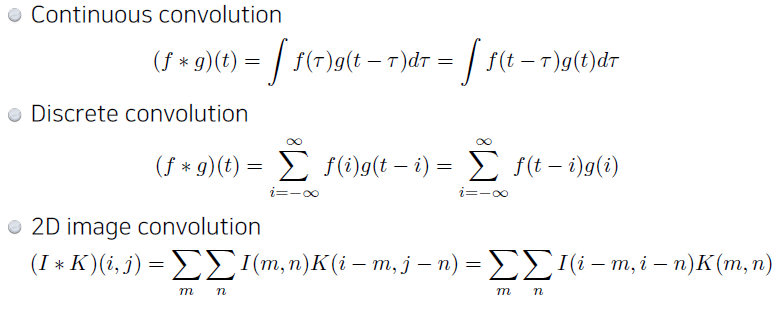
(x, y)는 출력 이미지의 좌표이며, i와 j는 커널의 좌표이다. 이 수식은 각 픽셀의 값을 커널과 이웃한 픽셀들의 선형 결합으로 계산하는 것을 의미한다. 여기서 f는 입력 신호 또는 이미지, g는 필터(또는 커널) 역할을 하는 함수이다. 합성곱은 f의 각 요소와 를 일정한 간격으로 이동하면서 곱한 후 모두 더하는 과정으로 이루어진다. 이미지의 경우, 2차원 합성곱을 사용하여 픽셀 간의 관계를 분석한다.
이산 합성곱에서 k가 음의 무한에서 양의 무한까지 가는 이유는 입력 신호 와 필터 의 전체 범위를 모두 고려해 합성곱을 계산하기 위해서이다. 실제 구현에서는 신호가 유한한 길이이므로, i는 신호의 시작부터 끝까지 한정되지만, 수식적으로는 전체 범위를 표현하기 위해 무한으로 나타낸다. 합성곱 연산의 핵심은 커널 를 뒤집어서 신호 에 차례로 겹치게 하고, 겹치는 부분의 곱을 더하여 값을 계산하는 것이다. 여기서 n−i는 필터 가 신호 의 특정 위치 에 올 때, 의 k번째 요소가 신호 f의 n−i번째 요소와 곱해짐을 의미한다. 즉, i가 증가하면서 가 신호 f에 점차 이동하는 방식이다.
신호 와 필터 이 있다고 가정하고 1차원 이산 합성곱을 계산하면 각 위치에서 필터가 뒤집힌 상태로 신호에 적용되면서 결과를 구한다. g가 [1,0,−1]이므로, 합성곱 연산에서 필터는 뒤집힌 상태인 [−1,0,1]로 적용된다. 필터 g의 인덱스 는 필터를 신호 f 위에서 이동시키며 적용하기 위해 사용되며, 는 필터의 각 요소가 신호의 어떤 위치에 대응하는지를 나타내는 인덱스이다. 이 값은 필터가 특정 위치에서 뒤집혀 겹치는 위치를 정의하여 필터링 과정에서의 신호 변형을 명확히 한다.
중요한 부분은, 컨볼루션 연산을 적용할 때 커널 h가 180도 회전된다는 점이다. 이는 컨볼루션의 특성에 의해 발생하는데, 커널이 이미지 위에서 이동하면서 연산될 때, 커널을 좌우 반전과 상하 반전을 통해 회전시킨 후 적용하는 것이 일반적인 방식이다. 이렇게 회전하는 이유는 수학적 정의에서 기인한 것으로, 커널이 이미지의 이웃 픽셀들과 적절하게 결합되도록 하기 위해서이다.
요약 : 컨볼루션 적용 과정에서는 먼저 커널 를 180도 회전한 후, 이를 이미지 위에서 각 픽셀 위치에 맞춰 슬라이드하며 적용한다. 각 위치에서 회전된 커널의 값과 이미지의 해당 부분 값을 곱하고, 이 결과들을 모두 더해 새로운 이미지의 해당 픽셀 값을 생성한다.
우리가 지금 컨볼루션에 도달한 이유는 이미지의 gradient를 구하고, 이를 통해 이미지 내 유의미한 객체의 에지(경계)를 파악하는 것이 목적이었다. 에지는 이미지에서 중요한 부분을 차지하며, 경계를 찾는 과정은 객체의 윤곽을 알아내는 데 큰 도움이 된다. 이 gradient를 구하기 위해 우린 기본적으로 간단한 차분을 사용해, 우측 픽셀값 - 좌측 픽셀값으로 계산할 수 있었다. 그러나 이 계산을 이미지 전체에 효율적으로 적용하기 위해 모든 픽셀에 대해 동일한 연산을 수행하는 필터(filter)를 생각하게 된 것이다. Linear filter란 각 픽셀을 그 이웃한 픽셀들과의 가중합(weighted sum)으로 새롭게 계산하는 연산이다. 이 연산을 모든 픽셀에 적용하여 이미지를 변환하는 방식이다. 그런데 이 과정에서 효율적으로 필터를 적용하기 위한 수학적 도구로 컨볼루션(convolution)을 사용하게 되었고, f와 h를 convolution하는 문제까지 도달했다.
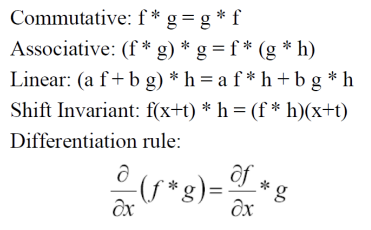
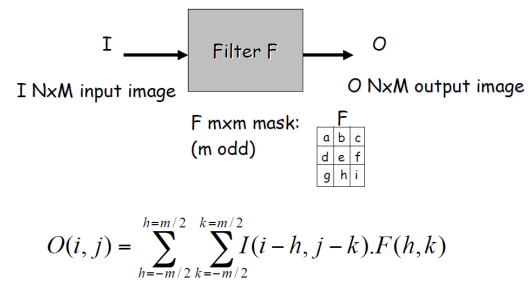
선형 필터링은 이미지의 각 픽셀을 주변 픽셀들과 가중합하여 새로운 값을 계산하는 기법으로, 컨볼루션과 Cross-Correllation 연산을 통해 수행된다. Convolution은 필터를 180도 회전시켜 적용하는 반면, Cross-coreelation은 필터를 회전하지 않고 그대로 사용하는 방식이다. 필터가 대칭적일 경우, 컨볼루션과 크로스-상관의 결과는 동일하며, 이를 통해 효율적인 필터링이 가능하다. 따라서 뒤집지 않고 필터링 하려면 필터를 Symmetric 하게 만들어 주면 된다.

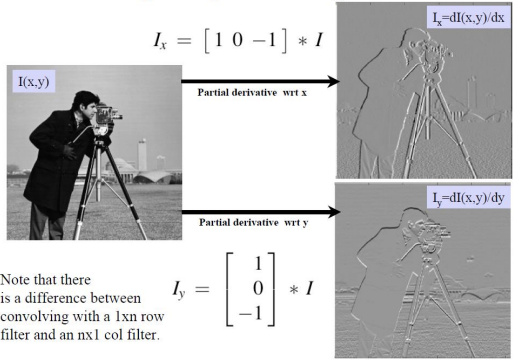
3. Derivates and Noise
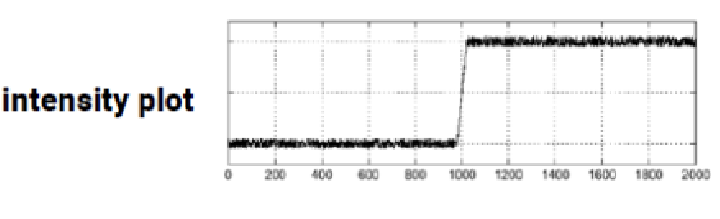
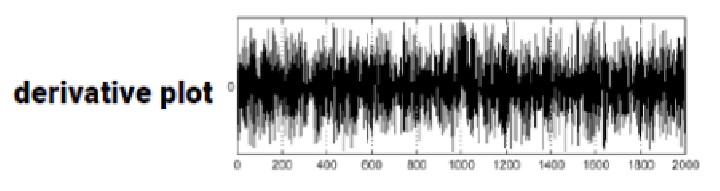
이미지에서 edge를 검출하기 위해 gradient를 구하면, high frequency때문에 에지를 검출할 수 없다.

이미지에서 에지를 검출하기 위해 Gradient를 구하는 것은 픽셀 값의 변화율을 계산하여 경계선을 강조하는 방법이다. 하지만, 고주파(high frequency) 성분이 많이 포함된 이미지는 노이즈가 많기 때문에, 그래디언트 연산을 수행할 때 작은 변화에도 큰 값이 나타나 노이즈가 에지로 잘못 인식될 수 있다. 이러한 고주파 성분들은 원치 않는 세부사항이나 잡음을 포함하고 있어 실제 에지와 구분이 어려워진다. Convolution 계산은 noise에 매우 민감하다. 따라서 Convolution 계산 전에 noise 제거가 거의 필수이다.
Image Noise
이미지 처리에서는 이러한 노이즈를 제거해 깨끗한 이미지를 얻는 것이 중요한데, 특히 systematic noise는 규칙적이거나 예측 가능한 성질을 지닌 노이즈를 의미한다. 예를 들어, 카메라 센서의 결함, 조명 조건의 변동, 또는 특정 장비의 반복적인 오류로 인해 발생하는 노이즈가 이에 해당한다. 이러한 시스템적인 노이즈는 패턴이나 특징이 명확해 예측 및 보정이 가능하며, 이를 제거하는 데 효과적인 필터링 기법이 존재한다. 그러나 assyematric noise는 예측할 수 없는 무작위 성질을 가지기 때문에 완전히 제거하기 어렵다. 이 때문에 처리 가능한 노이즈는 주로 시스템적이며, 나머지 비체계적 노이즈는 처리에 한계가 있어 완벽히 제거할 수 없다.
Modeling Image Noise
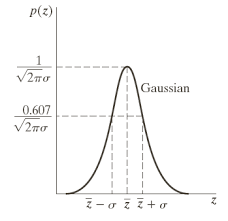
이미지에서 노이즈를 Gaussian 분포로 가정하는 이유는, 자연에서 발생하는 무작위적인 변동들이 Gaussian 분포로 설명되기 때문이다. Gaussian 노이즈는 평균이 0인 정규 분포를 따르며, 대부분의 노이즈 값이 0에 가깝고, 아주 큰 값은 거의 드물게 발생하는 특징이 있다. 예를 들어, 카메라 센서의 전자적 변동이나 조명 변화로 인해 발생하는 미세한 이미지 왜곡이 Gaussian 분포 형태를 띤다.
이 노이즈는 각 픽셀에서 독립적으로 발생하고, 모두 동일한 분포를 따른다고 가정된다. 이렇게 zero-mean Gaussian 노이즈는 이미지에 큰 영향을 주지 않고, 작은 무작위적 변동만을 일으키기 때문에 이미지의 원본 정보를 심각하게 왜곡하지 않는다.
Gaussian 분포(또는 정규 분포)는 통계학과 확률론에서 가장 널리 쓰이는 연속 확률 분포 중 하나로, 벨 모양의 곡선 형태를 가지며 수학적으로 매우 중요한 분포이다. 이 분포는 평균(μ)과 표준편차(σ)에 의해 완전히 정의되며, 평균은 데이터가 중심을 이루는 위치를, 표준편차는 데이터의 퍼짐 정도를 나타낸다. Gaussian 분포의 확률 밀도 함수는 다음과 같은 식으로 표현된다
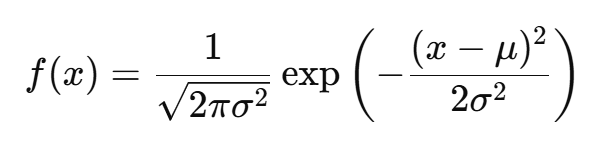
이 함수는 중심(평균 μ)을 기준으로 대칭 구조를 가지며, 값이 평균에 가까울수록 빈도가 높고, 평균에서 멀어질수록 빈도가 낮아지는 형태로 종 모양 곡선(Bell Curve)을 형성한다. 이러한 구조 덕분에 Gaussian 분포는 자연현상에서 관찰되는 많은 데이터의 변동성을 잘 설명한다. 예를 들어 사람의 키, 시험 점수, 센서의 미세한 잡음 등이 Gaussian 분포를 따르기 쉽다. 또한, 중심극한정리에 따르면 여러 독립적이고 동일한 분포를 따르는 확률 변수가 충분히 많아지면, 이들의 평균이 Gaussian 분포에 가까워진다.
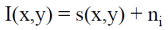
위 식은 촬영된 이미지 I(x,y)가 진실 데이터 s(x,y)와 가우시안 랜덤 변수 에 의해 왜곡된 경우를 다룬다. 여기서 공통적인 가정은 각 픽셀의 노이즈 이 모든 픽셀에서 독립적이고 동일한 분포(i.i.d)를 따른다는 점이다. 즉, 이미지의 각 픽셀에 발생하는 노이즈는 서로 상관관계 없이 개별적으로 발생하며 모든 픽셀이 동일한 확률 분포를 따른다. 이러한 i.i.d 가정을 통해 이미지에서 발생하는 노이즈가 특정한 패턴 없이 무작위적으로 나타나며, 평균이 0인 Gaussian 분포를 따르는 노이즈를 모델링할 수 있다. 이 가정은 필터링과 같은 노이즈 제거 기법을 적용할 때 이미지 전체에서 노이즈를 일관성 있게 처리할 수 있도록 돕는다. 두 번째 가정은 노이즈 n가 평균이 0인 가우시안(정규) 분포를 따른다는 것이다. 이는 노이즈가 평균적으로 양수와 음수가 동일하게 분포되며, 극단적인 값들이 발생할 가능성이 있지만, 대부분의 노이즈 값은 평균 근처에 집중된다는 것을 뜻한다.
여기서 각 픽셀의 노이즈 이 모든 픽셀에서 독립적이고 동일한 분포(i.i.d)를 따른다는 말은, 이미지의 각 픽셀에 있는 노이즈가 다른 픽셀의 노이즈에 영향을 주지 않고, 모두 같은 방식으로 발생한다는 뜻이다. 예를 들어, 사진을 찍을 때 카메라의 센서에서 발생하는 잡음이 있다면, 이미지의 한 픽셀에서 발생한 노이즈가 다른 픽셀의 노이즈에 영향을 미치지 않는다. 즉, 이미지의 모든 픽셀에 무작위적이고 독립적인 작은 노이즈가 개별적으로 추가된다. 이렇게 독립적인 노이즈가 모든 픽셀에 동일하게 분포하므로, 특정 픽셀에만 노이즈가 집중되거나 일정한 패턴을 띠는 것이 아니라, 이미지 전체에 걸쳐 고르게 퍼진다.
진실 데이터(ground truth)란 데이터의 실제 또는 이론적으로 정확한 값으로 측정하고자 하는 대상의 이상적인 상태를 의미한다. 예를 들어, 노이즈가 섞이지 않은 이미지가 진실 데이터라면 카메라 센서나 환경적 요인으로 인해 발생한 모든 노이즈가 제거된 상태의 순수한 이미지를 가리킨다. 이는 알고리즘이 정확히 무엇을 예측하거나 복원해야 하는지 기준이 되는 값으로, 모델의 성능 평가나 훈련 데이터로 주로 활용된다. 진실 데이터는 실제 데이터와 다를 수 있는 오류를 평가하고 교정하는 기준 역할을 한다.
Zero-mean Gaussian 노이즈를 제거하기 위해 여러 장의 사진을 평균화하는 방법은 같은 장면을 여러 번 촬영하여 각 이미지의 같은 위치 픽셀 값들을 평균내는 방식이다. 예를 들어, 밤하늘을 촬영한다고 가정해보자. 첫 번째 사진에는 무작위적인 Gaussian 노이즈가 별 부분에 조금 더 밝게, 배경에 약간 어둡게 나타날 수 있다. 두 번째 사진에는 이 노이즈가 다른 위치에 조금씩 다르게 나타난다. 이렇게 여러 장을 찍은 뒤 각 사진의 동일한 위치의 픽셀 값을 평균내면, 무작위적인 노이즈는 평균이 0에 가깝게 수렴하면서 상쇄된다. 반면에, 실제 별빛 같은 신호는 평균을 취해도 동일하게 유지된다. 이를 통해 신호가 유지되면서도 불필요한 노이즈가 줄어들어, 신호 대 잡음비(SNR)가 향상된 더 깨끗한 이미지를 얻을 수 있다.
Smoothing Reduces Noise
노이즈를 제거하기 위해서는 보통 Smoothing을 사용하며, 이는 여러 픽셀 값을 Averaging하는 방식으로 이루어진다. 만약 여러 장의 사진을 촬영할 수 있다면 카메라의 노출을 길게 하여 연속적으로 이미지를 수집하고 이를 평균화하여 노이즈를 제거할 수 있다. 그러나 단 한 장의 사진만 있을 경우, 같은 픽셀의 이웃 픽셀들과 평균화하여 smoothing을 할 수 있다. 이 경우, 각 픽셀이 독립적이고 동일한 분포(i.i.d.)를 따르지만, 이웃 픽셀들 또한 유사한 신호와 노이즈를 가질 것이라고 가정하여 서로의 값을 평균화해 노이즈를 줄이는 방법을 사용할 수 있다.
Averaging / Box Filter
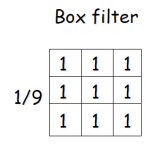
Sum이 1인 filter이며 모든 weight가 동일한 filter를 BOX Filter라고 부른다. Averaging을 통해 노이즈를 줄이는 이유는, 노이즈의 분산(variance)이 평균화 과정에서 줄어들기 때문이다. 개별 픽셀의 노이즈 분산이 σ2라면, 개의 픽셀을 평균내면 평균 노이즈의 분산은 σ2/m이 되어, 픽셀 수가 많을수록 노이즈의 분산이 감소한다. 즉 픽셀 noise의 variance보다 average noise의 variance가 더 작기 때문이다.
i.i.d.는 "independent and identically distributed"의 약어로, 확률 및 통계에서 자주 사용되는 용어이다. 이는 각 데이터 포인트가 서로 독립적(independent)으로 발생하고, 동일한 분포(identically distributed)를 따른다는 의미이다. 예를 들어, 이미지에서 각 픽셀에 발생하는 노이즈가 i.i.d.라고 하면, 모든 픽셀의 노이즈가 서로 영향을 주지 않으면서(독립적), 동일한 Gaussian 분포를 따른다는 뜻이다. 이런 가정은 노이즈 제거와 같은 통계적 처리를 할 때 분석을 단순하게 만들어주며, 많은 확률 모델의 기본 가정으로 쓰인다.

average noise의 분산 = pixel noise의 분산 / m 을 의미한다.
BOX Filter는 모든 weight가 동일하고 합이 1인 필터로 이미지의 작은 영역 내 픽셀 값을 평균내는 방식으로 노이즈를 줄인다. 예를 들어, 흐릿하게 촬영된 풍경 사진의 한 부분을 살펴보자. 여기서 BOX 필터를 사용하여 3x3 픽셀 영역의 값들을 평균낸다면 이 영역 내 각 픽셀에 있는 노이즈들이 합쳐져 평균화된다. 만약 각 픽셀에 있는 노이즈의 분산이 라면 이 3x3 영역을 평균낼 경우 결과의 노이즈 분산은 σ^2/9가 된다. 즉, 영역의 크기가 클수록 평균에 의한 노이즈 감소 효과가 커진다. 이렇게 평균화 과정을 통해 이미지 내 무작위적 노이즈가 상쇄되며 더 작은 분산을 가지게 되어, 결과적으로 전체적으로 더 부드럽고 깨끗한 이미지를 얻을 수 있다.
Box Filter와 같은 Smoothing 기법은 주변 픽셀들의 평균을 계산하여 이미지를 부드럽게 만드는 방법이지만 이 과정에서 중요한 디테일을 잃을 수 있다. 예를 들어, 세밀한 건물의 외관이 있는 도시 풍경 사진을 생각해보자. Box Filter를 적용하면 각 픽셀의 값이 주변 픽셀들의 평균으로 대체되면서, 건물의 경계선이나 창문 같은 고주파 성분이 감소하게 된다. 이로 인해 이미지의 선명한 윤곽이 부드러워지고 경계가 흐릿해지면서 전체적으로 과도하게 부드러운 효과가 발생한다. 또한, 이미지의 우측 상단 배경에서 발생하는 고주파 성분, 예를 들어 나뭇잎의 잔가지나 그림자 같은 미세한 변화도 필터링 과정에서 제거되어 원래의 디테일이 손실된다. 따라서 Box Filter를 통해 얻은 부드러운 이미지는 배경이 단조롭게 변형될 뿐만 아니라, 중요한 시각적 정보가 사라져 감상자에게 전달하고자 하는 메시지가 약해질 수 있다.

Low-pass 필터링은 이미지에서 값의 변동이 큰 고주파(high frequency) 성분을 제거하여 부드럽게 만드는 과정이다. 여기서 고주파란 인접한 픽셀 간 밝기나 색상 변화가 큰 영역을 뜻하며, 보통 이미지의 윤곽선이나 미세한 디테일을 포함한다. 반대로 저주파(low frequency)는 값의 변화가 적은 영역, 즉 하늘이나 벽처럼 색상과 밝기 변화가 완만한 부분이다. Low-pass 필터는 이러한 고주파 성분을 제거하면서 저주파 성분만 남기기 때문에 노이즈와 같은 빠른 변화 요소는 줄어들지만, 동시에 이미지의 미세한 디테일도 사라질 수 있다. 따라서 low-pass 필터링은 이미지의 부드러움을 높이는 대신, 텍스처와 윤곽선 같은 중요한 세부 정보가 손실될 수 있는 단점이 있다.
Gaussian Smoothing Filter
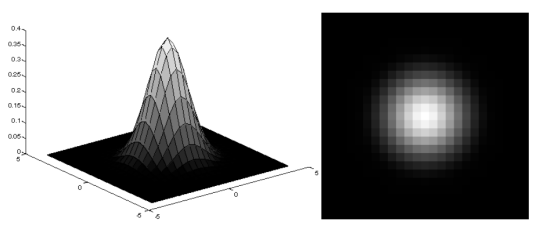
가운데 픽셀이 주인공인데 모두에게 동일한 값을 부여하는 것은 불공평하다. Gaussian Smoothing Filter는 이미지를 부드럽게 만들기 위해 사용되는 필터로, 중심 픽셀 주변의 픽셀들에게 가중치를 부여하여 평균을 계산하는 방식이다. 이 필터의 아이디어는 중심 픽셀에 상대적으로 큰 가중치를 주고 주변 픽셀에는 점진적으로 작은 가중치를 부여한다. 이는 가우시안 분포의 형태를 따르며 중심에서 멀어질수록 가중치가 감소하는 특징이 있다. 이렇게 함으로써 중심 픽셀의 값이 더 많은 영향을 받게 되어, 주변의 픽셀들에 의해 너무 큰 영향을 받지 않으면서도 부드러운 결과를 얻을 수 있습니다. 이 방식은 이미지의 세부사항을 적절히 유지하면서도 노이즈를 효과적으로 감소시킬 수 있습니다.
Gaussian Smoothing Filter는 이미지의 중심 픽셀 주변의 픽셀들에 가중치를 부여하여 평균을 계산함으로써 부드러운 이미지를 생성하는 방법이다. 예를 들어, 5x5 크기의 Gaussian 필터를 적용할 경우, 중심 픽셀의 위치에 있는 값은 높은 가중치(예: 0.4)를 부여받고, 주변 픽셀들은 가중치가 점진적으로 줄어들어(예: 0.2, 0.1) 적용된다. 이 필터를 사용하여 한 픽셀의 색상 값이 100, 주변 픽셀들의 값이 각각 80, 90, 70, 60, 75, 85, 65, 95라고 가정하면, 가중치를 적용하여 평균을 계산할 때 중심 픽셀에 더 큰 영향을 주게 된다. 계산은 다음과 같이 이루어진다. 이 과정을 통해 중심 픽셀의 값은 주변 픽셀들로부터 너무 큰 영향을 받지 않으면서도, 부드러운 결과를 얻을 수 있다. Gaussian Smoothing Filter는 세부 사항을 적절히 유지하면서 노이즈를 효과적으로 줄이는 데 유용하다.
Box vs. Gaussian

Gaussian Smoothing Filter
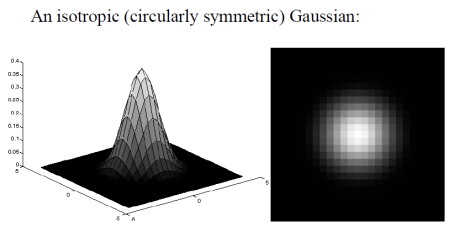
- Gaussian Smoothing at Different Scales



요약 : Gradient를 화살표로 나타내면, 화살표의 크기가 클수록 Gradient가 크고, 이는 밝기가 어두운 곳에서 밝은 곳으로 모인다는 의미이다. Gradient를 구하기 위해 Finite central difference를 사용하기로 했고, 이를 위해 Linear filtering을 적용해 이웃 픽셀들의 가중 합을 중심 픽셀에 업데이트한다. Convolution을 통해 linear filtering을 수행하며, 결과가 180도 회전하지 않도록 Symmetric한 Filter를 사용해 Cross correlation을 진행한다. 그러나 미분이 노이즈를 증폭시키기 때문에 Smoothing이 필요하며, 처음에는 Box filter를 사용해 Averaging을 통해 Smoothing을 시행한다. Box filtering은 Low-pass filtering으로 고주파 성분을 제거하며, Averaging이 노이즈를 줄이는 이유는 픽셀 노이즈의 분산보다 평균 노이즈의 분산이 작기 때문이다. 그러나 box filter는 모든 픽셀에 동일한 가중치를 부여하므로, Gaussian smoothing filter를 통해 중심 픽셀에 더 큰 가중치를 주어 주변 픽셀과의 차이를 줄이고자 하는 것이다.

Smooth before Applying Derivate Operator

이미지에 직접적으로 미분 연산자를 적용하면 노이즈와 작은 변동이 증폭되어 잘못된 에지나 특징을 생성할 수 있다. 이러한 효과를 완화하기 위해, 일반적으로 저주파 필터와의 convolution을 통해 smoothing 연산을 먼저 적용하여 고주파 노이즈를 줄이고 이미지의 기본 구조를 유지한다. 이 smoothing 연산은 이미지를 흐리게 하여 이후의 미분 연산이 노이즈보다는 강한 강도의 변화를 집중하도록 한다. 두 개의 선형 연산 smoothing(convolution을 통해)과 미분(미분 필터와의 convolution을 통해)을 수행하는 것처럼 보일 수 있지만, 이러한 순차적인 접근은 에지 검출의 견고성을 개선하고 결과를 더 신뢰할 수 있도록 하기 위해 필요하다. 그렇다면 이미지 처리에서 smoothing과 differentiation을 수행하기 위해 두 번의 convolution 연산을 적용해야 하는가?
Smoothing and Differentiation

Convolution operator의 associativity 속성을 이용하면 여러 필터를 하나의 필터로 합성할 수 있으며 이는 계산 효율성을 높이고 다양한 이미지 처리 효과를 얻는 데 유리하다. 예를 들어, 두 필터 g와 를 합성하여 새로운 필터 를 만든 후, 이미지를 필터 로 처리하면, 와 를 각각 적용한 후 결과를 얻는 것과 동일한 결과를 얻을 수 있다. 이러한 필터 합성을 통해 복잡한 효과를 간편하게 구현할 수 있다.
First(partial) Derivate of a Gaussian
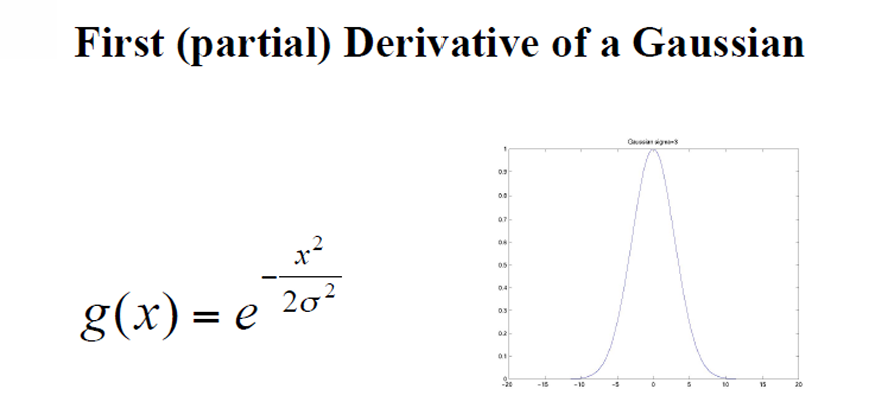
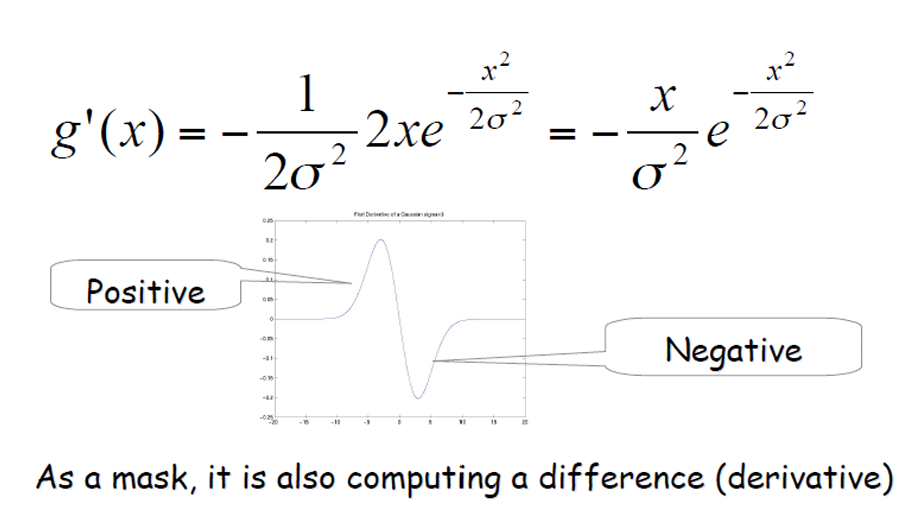
가우시안 필터는 원래 이미지를 부드럽게 하여 노이즈를 줄이는 데 사용되지만, 이 필터의 미분값을 계산함으로써 이미지의 경계나 특징을 강조할 수 있다. 가우시안 필터의 미분은 이미지의 밝기 변화에 대한 정보를 제공하여, 이미지의 특정 부분에서 강한 변화가 있는지를 나타낸다. 이 미분값을 사용하여 에지를 검출하면, 강한 밝기 변화가 있는 위치를 정확하게 식별할 수 있다.
Derivate of Gaussian Filter
우리의 목표는 gradient가 큰 곳, 즉 에지를 찾는 것이었다. 하지만 gradient convolution은 노이즈에 매우 민감하여 잘못된 결과를 초래할 수 있다. 이를 해결하기 위해 먼저 smoothing을 적용하기로 했고, 가우시안 필터를 사용하여 이미지를 부드럽게 만들 것이다. 이렇게 smoothing된 이미지에 미분 필터를 적용하여 강한 밝기 변화가 있는 지점을 찾아낼 수 있다. 그러나 smoothing filter와 derivative filter를 별도로 적용하는 대신, Derivative of Gaussian (DoG) 필터를 사용하여 두 과정을 한 번에 수행함으로써 효율적으로 에지를 검출할 수 있다.
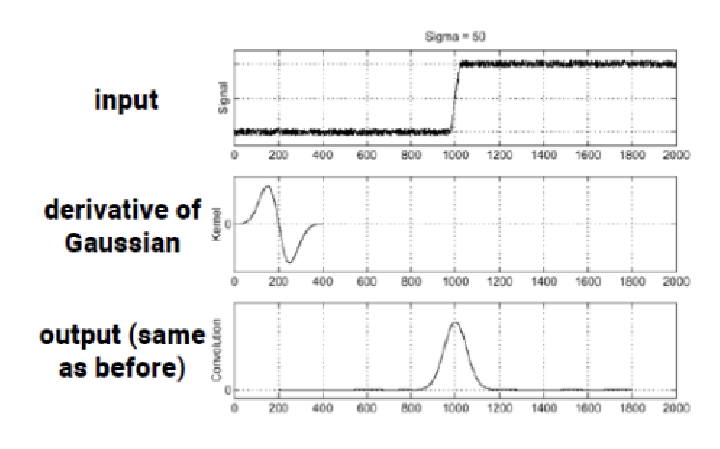
이전에 가우시안 필터를 적용한 후 미분 필터를 적용한 결과와 Derivative of Gaussian (DoG) 필터를 적용한 결과가 동일하다는 점을 알 수 있다. 이는 가우시안 필터를 통해 이미지를 부드럽게 한 뒤, 미분 필터로 강한 밝기 변화가 있는 지점을 찾는 두 과정을 DoG 필터를 사용하여 한 번에 수행할 수 있음을 의미한다. 이로써 smoothing과 intensity 변화 탐지를 동시에 진행할 수 있어, 전체적인 계산 비용을 줄이고 처리 효율성을 높일 수 있다.
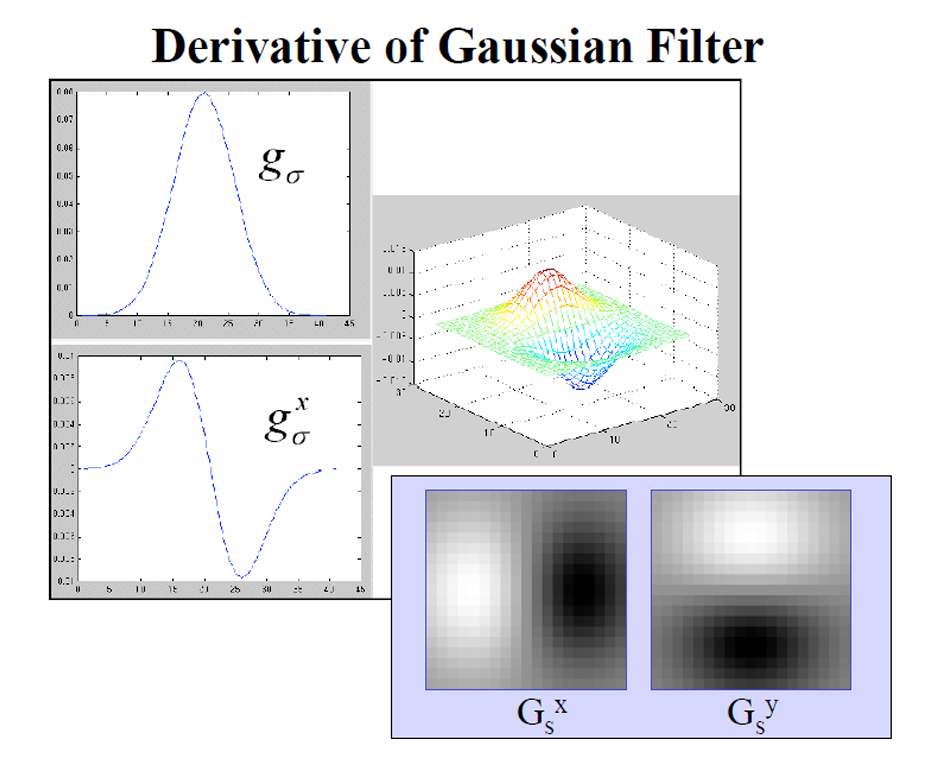
DoG필터를 사용하여 강한 밝기 변화가 있는 지점을 찾는 과정에서, 이 필터의 형태가 실제 에지와 유사하다는 점을 주목할 필요가 있다. DoG 필터는 자신의 gradient를 기반으로 gradient가 큰 곳, 즉 에지를 찾는 데 최적화되어 있다. 필터의 구조가 에지의 형태를 반영하고 있어 이 필터는 이미지에서 유사한 패턴이나 특징을 가진 부분을 효과적으로 탐지할 수 있다. 따라서 DoG 필터는 이미지 내에서 자기 자신과 유사한 지역을 찾는 데 도움을 주며, 에지 검출의 정확성과 효율성을 높이는 중요한 도구로 작용한다.
DoG(Difference of Gaussian) 필터의 형태가 실제 에지와 유사하다는 점은 필터의 구조가 에지를 감지하는 데 최적화되어 있다는 의미이다. 예를 들어, 이미지에서 사람의 얼굴 윤곽선을 검출한다고 가정해보자. 얼굴의 턱선은 어두운 색과 밝은 색의 경계가 뚜렷하게 구분되어 있으며, 이 경계는 강한 밝기 변화가 발생하는 지점이다. DoG 필터는 이러한 에지를 탐지하기 위해 두 개의 Gaussian 필터를 사용하여 이미지를 처리한다. 필터는 특정 형태(종종 종 모양)를 가지고 있는데, 이는 에지가 있는 영역에서 필터가 강조되는 방식과 같다. 즉, 필터의 중심은 강한 밝기 변화가 있는 부분을 강조하고, 주변은 상대적으로 감소시키는 방식으로 작동하여, 코와 턱의 경계 같은 실제 에지와 유사한 패턴을 인식하게 된다.
DoG(Difference of Gaussian) 필터를 사용해 이미지에서 강한 밝기 변화가 있는 지점을 찾는 과정은 필터의 구조와 밀접한 관련이 있는 것이다. 이 필터는 두 개의 Gaussian 필터를 서로 빼서 생성되며, 그 형태는 종 모양으로, 이미지 내에서 밝기 변화가 급격한 곳에서 강한 응답을 나타낸다. 예를 들어, 필터의 중심 부분은 높은 밝기와 낮은 밝기가 만나는 경계에서 가장 강하게 반응하게 설계되어 있다. 이로 인해 DoG 필터는 에지가 존재하는 위치, 즉 밝기 변화가 큰 곳에서 자신의 gradient를 기반으로 최대 응답을 하게 된다. 더 나아가, 필터의 구조가 실제 에지와 유사하다는 점은 필터가 자기 자신과 유사한 패턴을 찾는 데 효과적이라는 것을 의미한다. 즉, DoG 필터는 에지 형태를 반영하는 커널을 통해, 이미지 내에서 유사한 밝기 변화를 가진 지역을 찾아내는 데 최적화되어 있어, 에지 검출의 정확성과 효율성을 높이는 중요한 도구가 된다.
'Camera & Vision > Computer Vision' 카테고리의 다른 글
| Vision Theory [5] : 영상 분할 (0) | 2024.11.07 |
|---|---|
| Vision Theory [4] : 이미지 매핑 (0) | 2024.10.28 |
| Vision Theory[3] : 카메라 모델과 스테레오 비젼 (1) | 2024.10.13 |
| Vision Theory [2] : 에지 & 코너 검출 및 포인트 매칭 (2) | 2024.09.28 |
