
1. What are Edges?

이미지에서 밝기 변화가 급격히 일어나는 지점인 Discontinuities in intensity는 에지(edge)로 이는 물체의 형태와 구조를 정의하는 데 필수적이다. 예를 들어 풍경 사진에서 하늘과 땅의 경계선이 바로 에지의 대표적인 예가 된다. 이 에지는 하늘의 푸른 색상과 땅의 갈색 또는 녹색 사이의 갑작스러운 밝기 변화로 형성된다. 반면, 경계(boundary)는 이러한 에지를 통해 물체를 구분하는 의미 있는 경계 부분으로 볼 수 있다. 같은 사진에서 산의 경계선은 에지이기도 하지만, 그것이 특정한 산이라는 물체를 정의하므로 경계로도 이해될 수 있다. 이러한 경계는 물체 간의 구분을 명확히 하여 이미지의 의미를 전달하는 데 중요한 역할을 하며, 에지의 하위 집합으로서 물체 인식과 시각적 정보 전달에 기여한다.

에지는 밝기나 색상의 갑작스러운 변화로 인해 발생하는 부분으로, 주로 물체의 형태와 구조를 정의하는 데 기여한다. 예를 들어, 두 개의 서로 다른 색상의 영역이 만나는 지점에서 형성되는 선이나 윤곽이 에지다. 반면, 경계는 물체를 구분하는 의미 있는 구획을 나타내며, 에지의 하위 집합으로 볼 수 있다. 경계는 특정 물체를 식별하고, 물체 간의 관계를 명확히 하는 데 중요한 역할을 한다. 즉, 모든 경계는 에지를 포함하지만, 모든 에지가 경계인 것은 아니며, 경계는 물체 인식에 필요한 추가적인 정보와 의미를 제공한다.
Edge Detection (1D)

에지의 gradient는 에지가 얼마나 뚜렷한지를 나타내는 엣지인 정도(edgeness)로 해석할 수 있다. 즉, gradient 값이 클수록 에지가 더 분명하게 존재함을 의미한다. 그렇다면 이러한 gradient를 기반으로 에지를 판단하기 위해 특정 기준이 필요한데 이를 위해 threshold를 설정하여 gradient 값이 이 임계값을 초과하는 경우에만 에지로 간주하는 방법을 사용할 수 있다. 이 임계값은 에지를 검출하는 과정에서 노이즈와 실제 에지를 구분하는 중요한 역할을 하며, 적절한 threshold를 설정함으로써 에지 검출의 정확성을 높일 수 있다.
예를 들어, 이미지 처리에서 특정한 밝기 변화가 있을 때, 그 변화의 gradient 값이 일정 기준값인 threshold를 초과하면 해당 부분을 에지로 인식하는 방식이다. 만약 산의 경계선을 검출한다고 가정할 때, 산과 하늘의 색상 차이가 뚜렷해 gradient 값이 높다면, 이 값을 threshold로 설정해 그 이상의 gradient를 가진 지점을 에지로 판단할 수 있다. 반면, 경미한 변화는 에지로 간주하지 않고 제거함으로써 불필요한 노이즈를 줄이고, 정확한 경계를 찾아낼 수 있다. 이처럼 threshold 설정은 에지 검출의 정확성을 높이는 데 중요한 역할을 하며, 다양한 이미지와 상황에 따라 조정될 수 있다.
Overview of Gradients

gradient는 두 가지 주요 요소인 magnitude와 orientation으로 구성된다. magnitude는 이미지의 intensity 변화 강도를 나타내며 이는 에지의 뚜렷함을 나타내는 edgeness와 직접적으로 연결된다. 예를 들어, 밝은 색에서 어두운 색으로의 급격한 변화가 있을 경우, magnitude는 높게 측정되어 이 부분이 강한 에지를 형성하고 있음을 나타낸다. 반면, orientation은 intensity 변화가 가장 심한 방향을 지시한다. 즉, 에지가 존재하는 방향을 나타내며 이는 예를 들어, 수직 또는 수평 에지일 수 있다. 이러한 gradient는 수학적으로 기호 ∇I로 표현되며, 이는 특정 위치에서의 edgeness를 수치적으로 나타낸다. 따라서 ∇I는 해당 위치에서의 intensity 변화가 가장 두드러진 방향을 따르는 것이다.
에지 여부를 판단하기 위해 edgeness에 임계값(threshold)을 설정하는 것이 필요하다. 일반적으로 threshold를 낮게 설정하면 너무 많은 에지가 검출되어 원하지 않는 노이즈나 불필요한 정보까지 포함될 수 있다. 따라서 적절한 threshold를 설정해야 한다. threshold보다 edgeness가 큰 픽셀들에게 동일하게 1 값을 부여하면, 이때 비로소 에지가 검출된다. 예를 들어 특정 이미지는 처음에는 에지 이미지가 아니지만 threshold를 적용한 후에야 에지 이미지로 변환된다. 즉 원본 이미지는 여전히 edgeness 이미지만 포함하고 있으며 threshold를 설정하고 그에 따라 에지를 검출하는 과정이 필요하다.

위 이미지는 edge 이미지는 아니다. 왜냐하면 threshold를 준 다음에야 edge image가 된다. 아직까지는 edgeness 이미지이다.
Issues to Address Shotly

이미지 처리에서 edge를 판단할 때, threshold 값을 10으로 설정하면 여러 픽셀이 에지로 검출될 수 있어 이는 실제로 '선'이 아니라 특정 영역을 차지하는 "객체"로 잘못 인식될 수 있다. 에지는 본질적으로 선을 의미하며, 선은 면적을 갖지 않고 가능한 한 얇은 형태를 유지하는 것이 이상적이다. 예를 들어, 이미지에서 두드러진 경계를 가진 도형이 있다고 가정해보자. 만약 threshold가 너무 높아 여러 픽셀이 에지로 검출되면, 그 경계가 두꺼워져 왜곡된 모양을 형성하게 된다. 이러한 문제를 해결하기 위해 edge thinning 기법을 적용할 수 있다. 초기에는 낮은 threshold를 사용해 에지로 검출된 픽셀들을 수집하고, 그 후 edge thinning을 통해 두꺼운 경계를 얇게 만들어 실제 에지의 형태를 강조할 수 있다. 이 과정에서, 선의 형태가 보다 정교하게 다듬어지고 연결됨으로써 최종적으로 깨끗하고 뚜렷한 에지를 얻을 수 있다.
2. Canny Edge Detection

에지를 탐지할 때, 에지가 얇을수록 좋다는 원칙을 고려하여 threshold를 설정하는 대신 최대값을 찾는 방법을 사용할 수 있다. 이미지의 각 픽셀에서 intensity 값의 변화를 살펴보면서, 해당 픽셀과 이웃 픽셀 간의 값이 얼마나 변화하는지를 측정하면서 만약 특정 방향으로의 변화가 가장 큰 지점(즉, 극댓값)이라면, 그 지점이 강한 에지일 가능성이 높다. 이렇게 최대값을 찾으면, 에지를 구성하는 각 픽셀의 상대적인 중요성을 판단할 수 있어, threshold를 설정한 경우보다 더 세밀하고 정확한 에지 검출이 가능해진다.
이 경우, 이미지에서의 극댓값을 찾는 것은 에지의 뚜렷함을 높일 수 있는 접근이다. 하지만 극댓값을 구하기 위해 미분을 고려하게 되면 연산량이 매우 커지고 noise에 민감해질 수 있다는 단점이 있다. 따라서 더 효과적인 방법으로, threshold를 설정하여 남은 픽셀들을 대상으로 최대값을 구하는 방식이 유용하다. 예를 들어 이미지에서 특정 방향(orientation)의 에지를 검출한 후, 그 방향으로 픽셀들을 잘라내어 남은 영역에서 최대값을 찾는 과정을 생각해볼 수 있다. 이렇게 하면, noise의 영향을 줄이고 보다 선명하고 얇은 에지를 추출할 수 있으며 에지가 강조된 이미지 결과를 얻을 수 있다. 이를 통해 에지의 특성을 잘 반영하면서도 계산의 효율성을 유지할 수 있다.
Trade-off: Smoothing vs. Localization

Complete Canny Algorithm
Canny 알고리즘은 이미지에서 에지를 검출하는 데 효과적인 방법으로, 여러 단계를 통해 정확한 결과를 도출한다. 첫 번째 단계는 입력 이미지를 x 방향과 y 방향으로 편미분하여 두 개의 gradient 영벡터(I'x, I'y)를 구하는 것이다. 이를 통해 각 픽셀의 intensity 변화량을 파악할 수 있다. 다음으로, 모든 픽셀에서의 edgeness를 계산하여 gradient magnitude, 즉 |∇I|를 구한다. 이는 각 픽셀이 에지를 얼마나 강하게 나타내는지를 나타내는 수치이다. 그 다음, gradient의 방향(orientation)에서 지역 최대값(local maxima)만을 남겨, 가장 뚜렷한 에지 후보들만 선택한다.
이후 Hysteresis Thresholding 단계에서 두 개의 threshold(T'h와 T'l)를 사용하여 강한 에지와 약한 에지를 구분한다. T'h를 이용해 강한 에지에 해당하는 픽셀을 확실히 남기고, 그 주변의 약한 에지 픽셀들은 T'l을 기준으로 판단하여 연결(linking)한다. 예를 들어, 강한 에지 픽셀에 인접한 약한 에지 픽셀이 있다면, 그 픽셀은 강한 에지의 연장선으로 간주되어 최종적으로 에지로 연결된다. 이렇게 함으로써 Canny 알고리즘은 노이즈에 강하고, 정확한 에지를 검출하는 데 있어 우수한 성능을 발휘하게 된다.
Canny 알고리즘의 구체적인 과정은 다음과 같다. 먼저 입력 이미지에 대해 x 방향(I'x)과 y 방향(I'y)으로 편미분을 수행하여 gradient 영벡터를 계산한다. 예를 들어, 특정 픽셀의 intensity 값이 급격히 변화하는 경우, 이 픽셀의 I'x와 I'y 값이 모두 높게 나타나며, 이후 이 값을 사용하여 gradient magnitude인 |∇I|를 구한다. 이 magnitude 값이 높을수록 해당 픽셀이 강한 에지로 인식된다. 다음으로 gradient 방향에 따라 지역 최대값을 추출하여 가장 뚜렷한 에지 후보만 남긴다. Hysteresis Thresholding 단계에서는 두 개의 threshold를 설정한다. T'h를 사용하여 강한 에지 픽셀을 식별한 후, 그 주변의 약한 에지 픽셀(T'l)에 대해, 강한 에지와 연결된 픽셀만 남긴다. 예를 들어, 강한 에지가 있는 픽셀에 인접한 약한 에지 픽셀이 있다면, 이 픽셀은 에지의 일부로 간주되어 최종 결과에 포함된다. 이러한 과정을 통해 Canny 알고리즘은 이미지에서 노이즈의 영향을 최소화하며, 신뢰할 수 있는 에지 검출 결과를 제공한다.
Non-maximum suppression
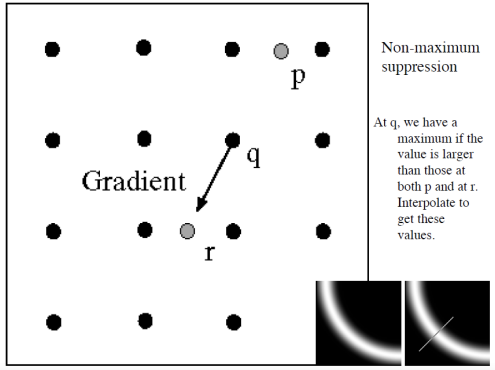
local maxima를 구하는 과정은 특정 픽셀이 주변 픽셀들보다 얼마나 두드러진 에지인지 판단하는 데 중요한 역할을 한다. 예를 들어, 픽셀 q의 gradient magnitude를 기준으로, q의 orientation(즉, 방향)에 위치한 두 개의 이웃 픽셀의 값과 비교한다. 만약 q의 값이 이 두 이웃 픽셀의 값보다 크다면, q는 지역 최대값(local maxima)으로 간주된다. 그러나 이때 q의 orientation에 해당하는 방향으로 더 큰 값이 존재한다면, q는 local maxima가 아니므로 그 값으로 업데이트된다.
구체적으로 설명하자면, q가 수평 방향의 gradient를 가진 경우, q의 위와 아래에 위치한 픽셀을 확인하고, q의 값이 두 픽셀의 값보다 크면 local maxima로 인정된다. 그러나 q의 오른쪽에 있는 픽셀의 값이 q보다 크다면, q는 local maxima로서의 지위를 잃고, 그 픽셀의 값으로 교체된다. 이 과정을 통해 Canny 알고리즘은 보다 정확한 에지를 검출하기 위해 지역 최대값을 신중하게 식별하여, 에지가 뚜렷한 부분만을 강조할 수 있도록 한다.
Hysteresis Thresholding

그래프의 y축이 gradient amplitude, 즉 |∇I|를 나타낸다고 할 때, Canny 알고리즘에서의 Hysteresis Thresholding 과정은 두 개의 threshold를 사용하여 에지를 선정하는 중요한 단계이다. 먼저, 설정한 high threshold보다 높은 gradient amplitude를 가진 영역을 에지로 선정한다. 예를 들어, 특정 이미지에서 gradient amplitude가 100인 픽셀은 high threshold가 80인 경우 강한 에지로 인식되어, 이 픽셀과 그 주변 픽셀들이 에지로 분류된다.
그 다음 단계에서는, 이미 에지로 선정된 영역의 주변을 살펴보고, low threshold보다 큰 gradient amplitude를 가진 픽셀을 추가로 에지로 선정한다. 예를 들어, 주변 픽셀 중에서 gradient amplitude가 60인 픽셀이 있다면, low threshold가 50인 경우 이 픽셀도 에지로 간주된다. 이렇게 강한 에지 주위에 위치한 약한 에지들이 연결되면서, 최종적으로 더 세밀하고 연속적인 에지 구조를 형성하게 된다. 이 과정은 이미지에서의 중요한 세부 사항을 잘 포착하여, 에지 검출의 신뢰성을 높이는 데 기여한다.
요약 : smoothing과 derivative filtering을 동시에 수행하기 위해 Derivative of Gaussian(DoG) 필터를 사용한다. 이 필터는 이미지에서 에지를 검출하기 위한 효과적인 방법으로, convolution을 통해 이미지의 특정 특징을 강조할 수 있다. DoG convolution을 수행하면 edgeness, 즉 magnitude(gradient amplitude)를 얻을 수 있으며, 이 정보를 바탕으로 에지를 찾기 위해 thresholding을 적용한다. 하지만 smoothing과 좋은 에지 로컬라이제이션은 항상 trade-off 관계에 있으므로, 보다 정교한 접근이 필요하다. 이를 위해 모든 픽셀에 대해 orientation 방향으로 local maxima를 탐색하여, high threshold를 사용해 강한 edgeness를 가진 영역을 에지로 선정하고, 이 에지로 선정된 픽셀 주변에서 low threshold보다 높은 값을 가진 픽셀들을 추가적으로 에지로 모은다. 이러한 방법을 통해, Canny 알고리즘은 노이즈의 영향을 최소화하면서도 명확하고 정확한 에지를 검출할 수 있게 된다.
Second-Derivate Filters

F(x)의 변곡점을 찾기 위해 2차 미분을 이용하는 방법은 매우 유용하다. 변곡점은 함수의 concavity가 변하는 지점을 의미하며, 이는 F''(x)에서 zero-crossing을 통해 파악할 수 있다. 그러나 이미지 데이터는 연속적이지 않고 이산적(discrete)인 특성을 가지므로, 이미지의 픽셀 값이 128보다 작거나 큰 지점을 찾아 교차하는 위치를 확인해야 한다. 이 과정의 장점으로는 2차 미분을 통해 1차 미분의 극댓값을 직접 찾아낼 수 있어, thresholding의 필요가 없어진다. 또한, 극댓값이 픽셀 하나에 해당하므로 thinning 과정이 필요 없어 간단하고 효율적이다.
하지만 이러한 접근 방식에는 단점도 존재한다. 미분을 통해 noise가 증가할 수 있으며, 이는 이미지 품질에 부정적인 영향을 미칠 수 있다. 예를 들어, 경계가 모호한 영역에서는 noise가 강하게 나타나 변곡점을 잘못 식별할 위험이 있다. 또한, 상대적으로 gradient가 작은 부분은 무시될 수 있어, 중요한 세부 사항이 누락될 가능성이 높다. 이런 한계 때문에, 변곡점을 정확히 찾기 위해서는 noise를 줄이고 gradient 정보를 보존하는 다른 전처리 기술이 필요할 수 있다.
Numerical Derivates

2차 미분에 근사화하는 식이다. 결과적으로 현재 위치값과 왼쪽&오른쪽 값이 필요한 것을 알 수 있다.
Central difference approx to second derivate
위 이미지를 자세히 보면 edge가 '흰->검' 이거나 '검->흰'인 것을 확인할 수 있다.
Edge Detection (1D to 2D)
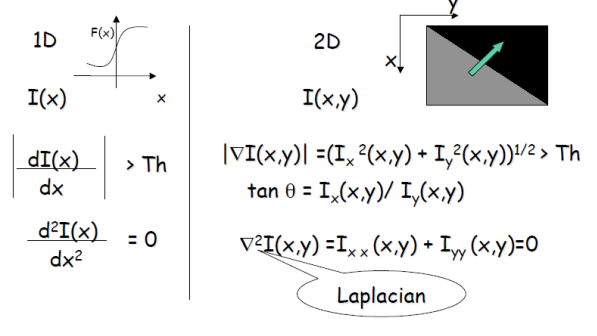
이미지 처리에서 ∣∇I∣는 이미지의 intensity 변화의 크기를 나타내며, 이는 에지의 강도를 측정하는 데 유용하다. 예를 들어, 밝은 부분에서 어두운 부분으로의 변화가 클수록 ∣∇I∣ 값이 커져 에지가 뚜렷하게 나타난다. 한편, tanθ는 gradient의 방향성을 의미하여 intensity 변화가 가장 큰 방향을 알려준다. 이를 통해 에지를 검출하고 특징을 추출할 수 있다.
Laplacian 연산자인 ∇2I(x,y)는 이미지의 이차 미분을 나타내며, 변곡점이나 에지를 찾는 데 특히 유용하다. 그러나 실제 이미지에서는 ∇2I가 정확히 0이 되는 경우는 드물다. 예를 들어, 한 픽셀 주변의 intensity 값이 변화하지 않는 경우 이론적으로는 Laplacian이 0이 되어야 하지만, 실제 이미지에서는 noise나 불완전한 샘플링으로 인해 미세한 변화가 발생하기 때문에 항상 0이 되지는 않는다.

이러한 특성 때문에 Laplacian은 개념적으로 에지의 위치를 나타내지만, 실제로는 noise에 민감하여 신뢰성을 고려해야 한다. 따라서 Laplacian을 사용할 때는 노이즈 제거와 같은 전처리 과정을 통해 더욱 정확한 에지 검출을 달성하는 것이 중요하다. 예를 들어, Gaussian smoothing을 통해 노이즈를 줄인 후 Laplacian을 적용하면, 더 명확한 에지를 검출할 수 있어 실제 이미지 처리에 효과적이다. 이미지의 픽셀 값에 대한 이차 미분을 근사하는 방식으로, Laplacian 연산자의 이산화된 형태가 주변 픽셀 값들과 중심 픽셀 값의 차이를 계산한다.
1. 이미지 선택: 먼저, 예를 들어 다음과 같은 간단한 5x5 이미지를 생각해 보자:
[ 10, 10, 10, 10, 10 ]
[ 10, 50, 50, 50, 10 ]
[ 10, 50, 10, 50, 10 ]
[ 10, 50, 50, 50, 10 ]
[ 10, 10, 10, 10, 10 ]
2. Laplacian 필터 적용: 다음으로, Laplacian 필터를 적용해 보자. 가장 일반적인 형태의 Laplacian 필터는 다음과 같은 3x3 커널이다:
[ 0, -1, 0 ]
[ -1, 4, -1 ]
[ 0, -1, 0 ]이 커널을 이미지의 각 픽셀에 적용하여 새로운 이미지를 생성한다. 커널을 중앙 픽셀에 맞춰 이동시키면서 각 위치에서의 값들을 곱해 합산한다.
3. 계산 과정: 예를 들어 (1, 1) 위치의 값을 계산해 보자. (50 위치) 주변의 픽셀 값과 Laplacian 커널을 곱한 후 합산하면 다음과 같다:
= (0 * 10) + (-1 * 10) + (0 * 10) +
(-1 * 10) + (4 * 50) + (-1 * 50) +
(0 * 10) + (-1 * 10) + (0 * 10)
= 0 - 10 + 0 - 10 + 200 - 50 + 0 - 10 + 0
= 120
4. 결과 해석: Laplacian 값이 120으로 계산된 위치는 강한 에지가 있다는 것을 나타낸다. 이처럼 Laplacian은 이미지의 변화를 강조하고, 에지가 존재하는 곳에서 큰 값을 산출하게 된다. 결과적으로 Laplacian 필터를 적용한 후에는 강한 변화가 있는 에지 부분에서 높은 값을 갖는 이미지가 생성된다. 이 이미지에서 값이 높은 픽셀들은 에지나 변곡점으로 간주할 수 있다.
이러한 과정을 통해 Laplacian 연산자가 이미지의 이차 미분을 계산하고, 경계 감지에 효과적으로 사용될 수 있음을 알 수 있다. 이를 통해 우리는 변곡점이나 에지를 효과적으로 탐지할 수 있게 된다.
Finite Difference Laplacian
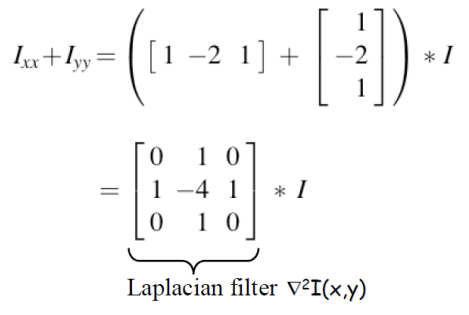
- Example

Laplacian 연산자는 이미지 처리에서 에지 검출에 자주 사용되지만, 몇 가지 한계가 있다. 예를 들어, 이미지를 이차 미분하여 intensity의 변화 곡률을 측정하지만, 이 과정에서 방향 정보가 소실된다. 즉, 에지가 수직인지 수평인지와 같은 중요한 정보를 알 수 없게 된다. 또한, 미분을 수행하는 과정에서 이미지의 noise가 더 두드러질 수 있기 때문에 주의가 필요하다.
이러한 문제를 해결하기 위해, Laplacian 연산을 적용하기 전에 Gaussian smoothing 필터를 사용하여 noise를 줄이는 것이 효과적이다. Gaussian smoothing은 이미지의 픽셀 값을 주변 값들과 평균 내어 부드럽게 만드는 과정으로, 이로 인해 noise가 감소하고 중요한 에지 정보를 더욱 뚜렷하게 만들 수 있다.
예를 들어, 한 이미지에 Gaussian smoothing을 적용한 후 Laplacian을 계산하면, 에지의 위치와 형태가 보다 명확하게 드러난다. 이는 실제로 에지 검출을 수행할 때, 원본 이미지의 noise로 인해 잘못된 에지나 왜곡된 정보가 나타날 수 있는 것을 방지할 수 있는 방법이다. 결론적으로, smoothing과 Laplacian을 결합하여 사용하는 것은 에지 검출의 정확성을 높이고 noise의 영향을 최소화하는 효과적인 방법이다. 이렇게 하면 에지 검출 결과가 더욱 안정적이고 신뢰할 수 있게 된다~이다.

LoG Filter
LoG(부드러운 Laplacian of Gaussian) 필터는 이미지 처리에서 에지 검출의 효율적인 방법으로 사용된다. 이 과정은 먼저 Gaussian 필터를 사용하여 이미지를 부드럽게 만드는 것에서 시작한다. Gaussian 필터는 노이즈를 줄이고, 이미지의 세부 정보를 보호하는 데 도움을 준다. 그 다음, 부드러운 이미지에 대해 Laplacian 필터를 적용하여 zero-crossing을 찾는다. 이는 이미지의 curvature 변화를 파악하여 에지의 위치를 식별하는 데 사용된다.
흥미로운 점은, Gaussian 필터를 통과시킨 이미지를 Laplacian으로 처리하든, Laplacian 필터를 미리 Gaussian으로 smoothing한 후 이미지를 통과시키든, 최종적으로 얻어지는 결과는 동일하다는 것이다. 예를 들어, 같은 이미지에 Gaussian smoothing을 적용한 후 Laplacian을 계산하면, 그 결과는 Laplacian of Gaussian 필터를 직접적으로 적용했을 때와 같아진다. 이러한 특성 덕분에 LoG 필터는 에지 검출 과정에서 계산 효율성과 정확성을 동시에 제공할 수 있으며, 두 가지 방법 중 어떤 것을 선택하더라도 유사한 성능을 기대할 수 있다.


1D Gaussian and Derivates
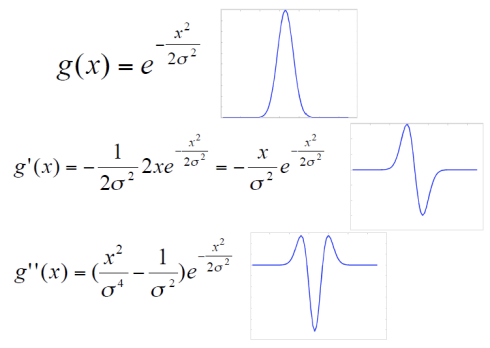
위 그림에서 최하단에 있는 그래프가 LoG filter이다.
Second Derivate of a Gaussian

1차 미분은 이미지의 변화량을 측정하여 경계선이나 윤곽을 강조하는 역할을 한다. 예를 들어, 이미지의 밝기가 급격하게 변하는 부분에서 1차 미분을 적용하면 그 부분이 더 뚜렷하게 드러난다. 2차 미분은 1차 미분의 결과를 다시 미분하여 이미지의 곡률 변화를 측정하고, 이는 노이즈나 작은 세부 사항을 제거하는 데 유용하다. 이러한 과정을 통해 2D 아날로그 이미지에 대해 컨볼루션을 수행하면, 이미지가 부드러워지면서 동시에 특정 특징이 강조된 결과를 얻을 수 있다. 예를 들어, 사진에서 배경은 흐릿하게 하고, 인물은 선명하게 남기는 방식으로 이미지 필터링을 통해 원하는 효과를 얻을 수 있다.
Efficient Implementation Approximating LoG with DoG
Laplacian of Gaussian(LoG)는 서로 다른 스케일을 가진 두 개의 가우시안 필터의 차이인 Difference of Gaussians(DoG)로 근사화할 수 있다. 이 방법은 가우시안의 분리 가능성과 연속성을 활용하여 LoG 연산자를 보다 효율적으로 구현할 수 있게 해준다. 두 개의 가우시안 필터를 적용하여 각각의 스케일에서 이미지를 처리한 후 그 결과를 빼줌으로써 이미지의 엣지와 같은 중요한 특징을 강조할 수 있는 대역 통과 필터링 효과를 얻을 수 있다.


가우시안 필터는 저주파 성분을 강조하고 고주파 성분을 제거하는 저역 통과 스무딩을 수행한다. 서로 다른 표준 편차를 가진 두 개의 가우시안 필터를 빼주는 과정을 통해 Laplacian of Gaussian(LoG)에 근사화할 수 있다. 이 방식은 이미지에서 고주파 노이즈를 제거하면서도, 경계나 엣지와 같은 중요한 세부 사항을 강조하는 데 유용하다. 예를 들어, 원본 이미지에 대해 넓은 표준 편차를 가진 가우시안 필터를 적용하여 부드럽게 한 후, 좁은 표준 편차의 가우시안 필터를 적용하여 세부 사항을 강조한 다음, 두 결과를 빼주면 LoG에 근사한 효과를 얻을 수 있다. 이를 통해 이미지의 경계가 더욱 뚜렷해지며, 중요한 형태나 패턴을 더 잘 인식할 수 있게 된다.
Efficient Implementation
Laplacian of Gaussian(LoG)는 두 개의 서로 다른 스케일을 가진 가우시안의 차이인 Difference of Gaussians(DoG)로 근사화할 수 있다. 이때 가우시안의 분리 가능성과 연속성을 활용하면 DoG의 효율적인 구현이 가능해진다. 예를 들어, 이미지 처리에서 일반적인 가우시안 필터는 저주파 성분만을 강조하는 저역 통과 필터로 작용하지만, 두 개의 가우시안 필터를 사용하여 서로 다른 스케일에서 이미지를 처리하고 그 결과를 빼면 LoG와 유사한 효과를 얻을 수 있다. 이 과정은 고주파 성분과 저주파 성분의 조합으로, 사실상 대역 통과 필터링을 구현하는 것과 같다. 예를 들어, 원본 이미지에 넓은 표준 편차를 가진 가우시안 필터를 적용하여 저주파 노이즈를 제거한 후, 좁은 표준 편차의 가우시안 필터로 얻은 결과를 빼줌으로써 이미지의 엣지나 중요한 특징을 강조할 수 있다. 이러한 접근 방식은 LoG 연산자를 더욱 효율적으로 구현하는 데 기여한다.
band-pass filter(대역필터): 특정 주파수 사이의 신호만 통과시킴
low-pass filter: 특정한 차단 주파수 이하의 신호만 통과시킴.
Maxima는 흰색, minima는 검은색으로 표시되며, 중앙 하단 쪽의 검은색 원처럼 주변 픽셀들과 다르게 고립된 포인트를 블롭(blob)이라고 한다. 이러한 블롭은 이미지에서 중요한 요소로 작용할 수 있다. 이전에 필터링은 커널의 형태와 유사한 포인트를 찾는 것과 같다고 언급한 바 있다. 이와 같은 맥락에서, LoG 필터(두 개의 가우시안 차이)는 블롭 형태를 갖고 있으므로, 블롭 검출에 효과적으로 활용될 수 있다. 즉, LoG 필터를 사용하면 이미지에서 고립된 블롭을 강조하고 검출할 수 있어, 객체 인식이나 이미지 분석에 유용한 도구가 된다.
LoG Blob Filtering
LoG 필터는 "블롭"을 찾는 데 유용하며, 여기서 최대값(maxima)은 밝은 배경에 있는 어두운 블롭을, 최소값(minima)은 어두운 배경에 있는 밝은 블롭을 나타낸다. 블롭의 크기는 LoG 필터의 시그마(sigma) 매개변수에 의해 결정되므로, 특정 크기의 블롭을 찾기 위해 시그마 값을 조절할 수 있다. 예를 들어, 얼굴을 검출하고 싶다면 얼굴 크기에 맞는 적절한 시그마 값을 설정해야 한다. 만약 더 작은 블롭, 즉 인물의 눈과 같은 세부 사항을 찾고 싶다면, 더 작은 시그마 값을 사용하여 커널 크기를 조절할 수 있다. 반면, 전체 몸통과 같은 큰 블롭을 찾기 원할 경우, 더 큰 시그마 값을 설정하면 된다. 이렇게 시그마 값을 조정함으로써 원하는 블롭의 크기에 맞춰 LoG 필터를 효과적으로 활용할 수 있다.

Observe and Generalize

필터로 컨볼루션을 수행하는 것은 찾고 싶은 특정 모양을 이미지에 적용하여 유사한 영역을 비교하는 것과 같다. 이러한 방식은 특징 탐지(feature detection)의 기초가 되며, 여기서 템플릿 매칭(template matching)이라는 개념이 등장한다. 템플릿 매칭은 내가 찾고자 하는 영역을 필터로 사용하여 이미지를 탐색하는 방법으로, 기본적인 탐지 기법으로 간주된다. 이 기법은 이미지를 이동(translation)하는 데 대해서는 강인성을 보여주어, 템플릿이 이미지 내에서 어디에 위치하든지 정확히 탐지할 수 있다. 그러나 회전(rotation)이나 크기 변화(scaling)에 대해서는 민감하게 반응하므로, 템플릿이 회전되거나 크기가 변할 경우 제대로 탐지하지 못하는 한계가 있다. 예를 들어, 얼굴 인식을 위해 템플릿 매칭을 사용하면, 정면 이미지는 잘 탐지하지만, 측면에서 촬영된 얼굴이나 확대된 얼굴 이미지는 정확하게 탐지하기 어렵다. 이러한 이유로 템플릿 매칭은 기본적인 탐지 기법이지만, 복잡한 이미지 변형에 대해서는 다른 기법과 결합하여 사용하는 것이 필요하다,
3. Corner Detection
What are Corners?

코너(corner)는 어떤 임의의 픽셀을 기준으로 특정 방향으로 움직일 때 변화를 인지할 수 있는 지점을 의미한다. 반면 엣지(edge)는 엣지 방향으로는 변화가 인지되지 않지만, 엣지 방향이 아닌 다른 방향으로 움직이면 변화를 감지할 수 있는 특성을 가진다. 평탄한 영역(flat)은 어떤 방향으로 움직이더라도 변화가 감지되지 않는 곳이다. 예를 들어, 그림에서 지붕 끝은 코너가 아닌 엣지로 분류될 수 있지만, 이는 3차원 공간에서의 관점이며, 2차원 평면에서는 코너로 인식될 수 있다는 점에 유의해야 한다. 즉, 2D에서의 엣지와 3D에서의 구조는 서로 다른 특성을 가지므로, 공간의 차원에 따라 인지되는 방식이 달라질 수 있다.
Motivation For Corner Finding
두 개 이상의 시점에서 촬영한 이미지 사이의 일치하는 특징(feature)을 찾는 과정에서 가장 쉽게 찾을 수 있는 지점은 코너(corner)이다. 따라서 코너를 먼저 찾아서 대응점(correspondence matching)을 수행하는 것이 일반적이다. 첫 번째 방법은 강인하게 인간이 직접 각 점을 선택하는 것이지만, 이는 명시적으로 문제를 해결하지 않는 비효율적인 방식이다. 두 번째 방법인 템플릿 매칭(template matching)은 특정 모양을 찾는 것으로, 이 또한 명시적인 문제 해결 방식이다.
코너를 찾는 것은 여러 가지 활용이 가능하다. 첫째, 이미지 속 물체의 배치와 구조를 파악할 수 있다. 둘째, 동일한 물체에 대한 대응점을 찾아 3차원 정보를 추정할 수 있다. 특히, 대응점을 많이 찾을수록 깊이(depth) 정보가 풍부해지므로, 3D 재구성 및 객체 인식 등의 작업에 유용하다.
Harris Corner Detector
Harris Corner Detecotr: Basic Idea

평탄한 영역은 정해진 패치(patch)를 어느 방향으로 이동하더라도 변화를 감지하기 어렵다. 이는 해당 영역이 균일하게 퍼져 있기 때문에 어떤 방향으로 움직이더라도 같은 값을 유지하기 때문이다. 반면, 엣지는 엣지 방향으로 이동할 경우 변화가 인지되지 않지만, 엣지 방향이 아닌 다른 방향으로 움직이면 변화를 감지할 수 있다. 마지막으로, 코너는 어떤 방향으로 이동하더라도 변화를 확실히 인지할 수 있는 특성을 가진다. 이는 코너가 이미지 내에서 방향이 급격히 바뀌는 지점이기 때문에, 이동하는 방향에 따라 강한 변화가 발생하기 때문이다. 이러한 특성들은 이미지 분석과 특징 탐지에서 중요한 역할을 한다.
Harris Detector: Mathematics

I(x,y)는 원본 패치의 세기(intensity)를 나타내고, I(x+u,y+v)는 이동된 패치의 세기를 나타낸다. w(x,y)는 윈도우 함수(window function)로, 특정 영역에 대한 가중치를 부여하여 패치의 중요도를 조정한다. E(u,v)는 두 패치 사이의 비유사성(dissimilarity)을 계산하는 함수로, 이 값이 클수록 해당 위치가 코너(corner)일 확률이 높아진다. 반면, E(u,v)의 값이 작을 경우 해당 위치가 평탄한(flat) 영역일 확률이 높아진다. 즉, 이와 같은 비유사성 측정을 통해 이미지 내에서 코너와 평탄한 영역을 구별할 수 있다.
Taylor Series for 2D Functions

매번 shift시켜서 dissimilarity를 계산하는 것은 많은 계산량을 요구하므로 비효율적이다. 이를 개선하기 위해 Taylor Series를 활용한 approximation을 사용할 수 있다. 예를 들어, 현재 위치에서의 intensity 값을 기준으로 주변 픽셀의 변화를 근사하는 방법이다. 만약 현재 위치에서의 intensity가 I(x,y)이고, 우리가 u와 v 방향으로의 변화를 고려할 때, Taylor Series를 통해 위와 같이 표현할 수 있다.
여기서 ∂I∂x/는 각각 x와 y 방향으로의 기울기(gradient)를 나타내며, 이는 현재 위치에서의 세기 변화율을 의미한다. 이렇게 하면, shift를 직접 수행하지 않고도 현재 위치의 정보만으로 주변 픽셀의 변화를 계산할 수 있어, 계산량이 크게 줄어든다. 이를 통해 feature detection과 같은 작업에서 효율성을 높일 수 있다.
Harris Corner Derivation
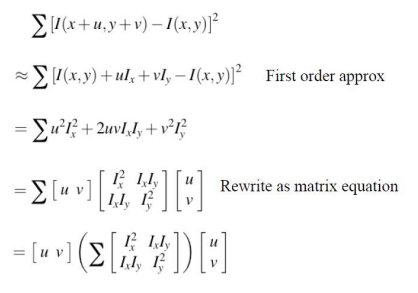
Harris Corner Derivation에서 나타나는 행렬은 이미지의 세기 변화에 기반한 코너 검출을 설명하며, 여기서 와 는 각각 이미지의 x 및 y 방향으로의 이동(shift)을 나타낸다. 예를 들어, 우리가 특정 이미지에서 코너를 찾고자 할 때, u를 1 픽셀, v를 0 픽셀로 설정하면, 이는 현재 위치에서 오른쪽으로 1 픽셀 이동한 위치의 intensity 값을 비교하는 것을 의미한다. 이 과정에서 행렬은 이동량에 따라 이미지의 세기 변화가 얼마나 이루어지는지를 측정하여, 특정 특징을 얼마나 잘 포착할 수 있는지를 판단하게 된다. 즉, 만약 코너가 존재한다면, u와 v 방향으로의 이동에 따른 세기 변화가 크게 나타나게 되고, 이는 코너 검출의 중요한 기준이 된다. 결국, 얼마나 이동(shift)해야 하는지가 이 계산의 핵심 입력값이 되어, 효과적으로 코너의 존재 여부를 평가할 수 있는 기반이 마련된다.
Harris Detector: Mathematics


와 vv 우리가 시도하는 이동(shift) 값이며, 결국 코너인지 엣지인지의 특징을 지닌 것은 M 행렬이다. 이 M 행렬은 우리가 원하는 정보를 포함하고 있어, 그 값이 의미가 있다면 M은 풀 랭크(full rank)를 가질 것이다. 풀 랭크라는 것은 두 개의 고유값(eigenvalue)이 모두 의미 있는 값을 가진다는 것을 의미한다. 각 고유값은 주어진 방향으로 이미지 세기가 얼마나 빠르게 변하는지를 나타내는 정보를 담고 있어, 이를 통해 해당 픽셀이 코너인지 엣지인지 평탄한지 구별할 수 있는 중요한 단서가 된다.


M 행렬의 고유값(eigenvalues)을 이용해 이미지 포인트를 분류할 수 있다. 두 개의 고유값이 모두 작으면 이미지의 세기가 모든 방향으로 거의 일정하다는 것을 나타내며, 이는 평탄한(flat) 영역을 의미한다. 반면, 두 고유값 중 하나가 다른 하나보다 크면 특정 방향으로만 변화가 크다는 것을 나타내며, 이는 엣지(edge)를 의미한다. 마지막으로, 두 고유값이 모두 크면 두 방향으로 모두 변화가 크다는 것을 나타내며, 이는 코너(corner)를 의미한다. 이러한 고유값 기반 분류는 이미지 내에서 특징적인 요소를 효과적으로 식별하는 데 중요한 역할을 한다.
요약
F(x)의 변곡점은 기울기(gradient)가 크게 변하는 지점으로, 이를 찾기 위해 2차 미분을 고려했으나, 미분 과정에서 노이즈가 증폭되고 연산량이 증가하는 문제가 발생했다. 그래서 Laplacian을 사용하여 근사화하려 하였고, 이로 인해 Laplacian 필터가 도출되었다. 이미지에 Gaussian 필터로 컨볼루션한 후에 Laplacian을 적용하면, Gaussian 필터에 Laplacian을 먼저 적용한 후 이미지에 컨볼루션하는 방식이 결과적으로 동일하다는 점이 확인되었다. 따라서 우리는 Laplacian of Gaussian(LoG) 필터를 사용하기로 하고, 이를 이미지에 적용했다. LoG 필터를 통과한 이미지는 LoG 필터와 유사한 형태의 블롭(blob)을 감지하게 되며, 필터로의 컨볼루션은 우리가 찾고자 하는 "모양"과 이미지의 유사한 영역을 비교하는 과정이 된다. 이렇게 특징 탐지가 시작되었고, 템플릿 매칭(template matching을 배우게 되었다. 템플릿 매칭은 이동(translation)에는 강인하지만 회전(rotation)이나 크기 변화(scaling)에 취약하다. 서로 다른 시점에서 촬영한 두 이미지 간의 대응점(correspondence matching)을 찾는 과정에서, 평탄한(flat) 영역은 어떤 방향으로 이동해도 변화를 감지할 수 없고, 엣지(edge)는 엣지 방향으로 이동할 때만 변화를 감지하지 못하며, 코너(corner)는 어떤 방향으로 이동해도 변화를 인지할 수 있다는 점이 중요하다. 따라서 코너를 먼저 탐지하기로 했다. 이미지의 세기를 u,vu, v 방향으로 이동시키며 비유사성(dissimilarity)을 계산하는 과정에서, 비유사성이 클수록 코너일 확률이 높고, 작을수록 평탄할 확률이 높다는 것을 알 수 있다. 하지만 이동하며 계산하는 과정은 번거로우므로, Taylor Series로 근사화하여 계산하겠다. 근사화된 식을 바탕으로 정리해본 결과, 유의미한 정보는 M 행렬에 저장되고 있다는 것을 발견했다. M 행렬의 고유값(eigenvalue)을 구하여 두 값의 크기를 비교함으로써 평탄한지, 엣지인지, 코너인지를 판별할 수 있게 된다.
Correspondence Problem
스테레오 및 모션 추정과 같은 비전 작업은 두 개 이상의 시점에서 correspondence features를 찾아야 한다. 예를 들어, 두 개의 카메라로 촬영한 이미지에서 코너를 찾으면, 객체의 형상이나 구조를 파악할 수 있다. 이는 코너가 객체의 중요한 특징을 나타내기 때문이다. 같은 객체를 찾고 correspondence point를 매칭하면, 두 이미지 간의 위치 변화로부터 깊이 정보를 추정할 수 있다. 예를 들어, 왼쪽 이미지에서 특정 코너와 오른쪽 이미지에서 해당 코너를 찾았다면, 두 점 사이의 거리와 카메라 간의 간격을 이용해 3D 공간에서의 위치를 계산할 수 있다. 이러한 correspondence point를 많이 찾을수록 깊이 정보가 풍부해져 3차원 정보를 보다 정확하게 추정할 수 있다. 이 과정은 실제 환경의 깊이와 구조를 이해하고, 이를 기반으로 다양한 응용 프로그램에 활용될 수 있다.
Correspondence Problem은 두 개의 이미지에서 일치하는 요소를 찾는 과제이다. 이 문제를 해결하기 위한 기본 가정은 대부분의 장면 점들이 두 이미지에서 모두 보여야 하며, 해당 이미지 영역들이 유사해야 한다는 것이다. 이러한 가정이 성립하려면 카메라와 객체 간의 거리가 멀어야 하며, 형상 변형이 없어야 한다. 따라서, 우리는 비교할 요소로 대응하는 점(corresponding point)을 선택하고, 이들 간의 유사성을 판단할 수 있는 유사도 측정 방법을 선택해야 한다. 알고리즘은 크게 두 가지로 나뉜다. 첫 번째는 상관관계 기반 알고리즘으로, 유사한 부분을 모두 찾는 밀집(DENSE)한 일치 집합을 생성한다. 이러한 방법은 3D 재구성에 유용하다. 예를 들어, 지형의 3D 모델을 만들기 위해 여러 지점에서 특징을 포착할 수 있다. 두 번째는 특징 기반 알고리즘으로, 대략 40개 정도의 유사한 부분을 찾는 희박(SPARSE)한 일치 집합을 생성한다. 이 방법은 강건성(robustness)이 뛰어나, 잡음이나 부분적 가림에 덜 영향을 받는다. 예를 들어, 사람의 얼굴 인식 시스템에서 주요 특징점만을 사용해 일치성을 판단할 수 있다. 이처럼 두 가지 접근법은 각각의 장점이 있으며, 상황에 따라 적절히 선택하여 사용할 수 있다.
Correlation-based Algorithms

4개의 패치 중에서 가장 유사한 패치를 찾기 위해서는 두 가지 요소가 필요하다. 첫째, 유사도 함수(similarity function)가 필요하다. 이 함수는 각 패치 간의 유사성을 수치적으로 측정하는 데 사용되며, 예를 들어, 제곱합 오차(Sum of Squared Differences, SSD)나 상관관계(correlation)와 같은 방법이 있다. 둘째, 가장 높은 유사도를 구하기 위한 검색 전략(search strategy)가 필요하다. 이는 주어진 패치와 비교할 패치를 선택하고, 유사도 함수를 적용하여 최적의 패치를 찾는 과정이다. 예를 들어, 브루트포스(brute-force) 검색 방식으로 모든 조합을 비교하거나, 효율성을 높이기 위해 휘발성 데이터 구조를 활용하여 탐색 범위를 줄이는 방법이 있다. 이러한 두 가지 요소를 통해 최종적으로 가장 유사한 패치를 효과적으로 찾을 수 있다.
Comparing windows

Example

cross-correlation을 이용해 template matching을 하려고 한다.

cross-correlation 결과, 일치하는 곳과 다른 곳에서 유사도가 가장 높게 나왔다.
Problem with Correlation of Raw Image Templates
Consider correlation of templates with an image of constant grey value:

Now consider correlation with a constant image that is twice as bright.

상수 회색 값의 이미지와 템플릿 간의 상관관계를 고려할 때, 템플릿과 이미지의 유사성을 측정하는 결과는 템플릿의 모양에 따라 달라지지 않는다. 그러나 이미지를 두 배 밝게 만들면, 모든 픽셀 값이 증가하여 상관관계 값이 높아질 수밖에 없다. 예를 들어, 템플릿이 특정 패턴을 가지고 있을 때, 그 패턴이 상수 회색 값의 이미지와 잘 맞더라도, 밝기가 두 배가 된 이미지와의 상관관계에서는 단순히 밝기 차이로 인해 높은 값을 얻게 된다. 이는 템플릿과 패치 간의 실제 유사도를 정확하게 반영하지 못하는 문제를 발생시킨다. 이러한 문제를 해결하기 위해, 이미지의 평균 밝기를 빼주는 방법이 효과적이다. 즉, 템플릿과 이미지 간의 상관관계를 계산하기 전에 각 픽셀에서 평균 밝기를 제외하면, 밝기 변화의 영향을 제거할 수 있어 실제 패턴의 유사성을 더 잘 반영할 수 있다.
Correlation, zero-mean template

가장 높은 점수가 정확한 매치가 아닐 경우, 물리적 제약(예: 카메라 위치 변화)을 추가하여 해당 영역 주변에서 매칭을 탐색하는 것이 필요하다. 이를 위해 SSD(Sum of Squared Differences) 또는 블록 매칭 방법을 사용할 수 있다. SSD는 두 이미지 간의 차이를 측정하는 방법으로, 특정 패치의 픽셀 값 차이를 제곱하여 모두 합산하는 방식이다. 이렇게 계산된 값이 작을수록 두 패치가 유사하다는 의미이다. 따라서, SSD를 사용하여 각 패치의 유사성을 평가하고, 물리적 제약을 고려하여 인접한 영역에서 최적의 매치를 찾음으로써 보다 정확한 결과를 얻을 수 있다. 이 방법은 블록 매칭을 통해 객체의 움직임이나 형태 변화를 효과적으로 추적하는 데 유용하다.

Relation between SSD and Correlation

상관(correlation)은 값이 클수록 두 요소가 유사하다는 것을 의미한다. 반면, SSD(Sum of Squared Differences)는 두 이미지 또는 패치 간의 차이를 측정하는 방법으로, 값이 작을수록 유사함을 나타낸다. 즉, SSD가 작다는 것은 두 이미지의 픽셀 값 차이가 적다는 것을 의미하며, 이는 해당 패치가 서로 비슷한 특징을 가진다는 것을 나타낸다. 따라서, SSD와 상관관계는 서로 반대의 지표로 작용하며, 유사성을 평가할 때 각각의 방법을 적절히 활용하여 최적의 매칭을 찾아낼 수 있다.
SSD

드디어 SSD(Sum of Squared Differences)를 사용하여 highest score와 correct match가 일치하게 되었다. 그러나 하나의 객체를 다른 각도에서 촬영할 경우, 밝기(intensity) 외에는 변화가 없어야 하는데, 이러한 제약 조건이 있음에도 불구하고 correspondence problem에서 밝기 정보의 변화는 패턴 인식을 어렵게 만든다. 이를 해결하기 위해 두 이미지 간의 correspondence point를 찾기 위해서는 intensity normalization을 적용해야 한다. 이 과정에서는 먼저 이미지의 평균 밝기를 빼고, 그 후 표준편차로 나누어 주어 밝기 차이를 최소화함으로써, 두 이미지의 유사성을 보다 정확하게 평가할 수 있게 된다.


두 이미지의 밝기 차이가 클 때, 첫 번째 그래프와 같이 zero-mean(평균을 빼는 과정)을 적용하여 두 번째 그래프처럼 변환한 후, 표준 편차로 나누어 세 번째 그래프처럼 밝기 범위를 맞춰준다. 하지만 한 이미지가 RGB 색상을 모두 포함하고 있는 반면, 다른 이미지는 R 채널만 제공하는 경우에는 correspondence problem을 해결하기 어려워진다. 이러한 상황에서는 shape 정보나 edge 정보를 활용하여 매칭을 찾는 방법이 필요하다. 그러나 일반적인 경우에는 위와 같이 zero-mean과 normalization을 통해 두 이미지의 밝기 정보를 일치시킴으로써 보다 정확한 correspondence point를 찾을 수 있다.
요약
일치하는 영역을 찾는 데 코너를 이용하는 것은 편리하며, 이를 통해 correspondence problem을 해결하고자 한다. 이 과정에는 두 가지 방법이 있으며, 하나는 DENSE하게 찾는 방법으로, 일치하는 모든 곳을 찾는 데 사용되며 3D reconstruction에 유리하다. 다른 하나는 SPARSE하게 찾는 방법으로, 예를 들어 일치하는 영역을 50개만 찾는 방식이며, 더 robust하다는 장점이 있다. 첫 번째 이미지의 특정 패치가 두 번째 이미지의 여러 패치 중 어떤 것과 일치하는지를 판단하는 방법으로는 SSD(Sum of Squared Differences)와 correlation이 있다. correlation 값이 클수록 유사성을 나타내고, SSD 값이 작을수록 유사성을 나타낸다. 만약 correlation을 이용해 highest point를 찾았지만 올바른 매치와 일치하지 않는다면, physical constraint를 추가해 해결할 수 있다. 일반적으로 SSD는 correlation보다 더 정확한 편이다. 또한, 두 이미지 사이의 intensity 차이나 range 차이가 크면, zero-mean 처리를 한 뒤 normalization(표준편차로 나눔)을 통해 두 이미지의 intensity를 일치시켜야 한다.
'Camera & Vision > Computer Vision' 카테고리의 다른 글
| Vision Theory [5] : 영상 분할 (0) | 2024.11.07 |
|---|---|
| Vision Theory [4] : 이미지 매핑 (0) | 2024.10.28 |
| Vision Theory[3] : 카메라 모델과 스테레오 비젼 (1) | 2024.10.13 |
| Vision Theory [1] : 이미지의 정보와 처리 (3) | 2024.09.19 |