
컴퓨터 비전에서 3D 정보 추출과 영상 처리를 위해서는 카메라 모델과 스테레오 비전을 이해할 필요가 있다. 카메라 모델은 실제 세계의 3D 정보를 2D 이미지로 투영하는 과정을 수학적으로 설명하는데, 이를 통해 이미지 내 객체의 위치나 크기를 추정할 수 있다. 스테레오 비전은 두 개의 카메라를 사용해 두 이미지 간의 차이를 비교하여 깊이 정보를 계산하며, 이를 통해 3D 재구성, 물체 탐지, 로봇 비전, 자율 주행 등 다양한 응용에 사용된다. 따라서 카메라 모델과 스테레오 비전의 원리를 이해하면 3D 공간에 대한 정확한 정보를 추출하고 다양한 응용에 활용할 수 있다.
Camera Model
카메라 모델은 컴퓨터 그래픽스를 배울 때 거의 다루었던 내용지만 컴퓨터 비전에서는 다르게 활용이 된다. 컴퓨터 그래픽스에서는 3D 장면을 2D 화면에 렌더링하기 위해 가상의 카메라를 사용하며, 투영 변환을 통해 시점을 조절하고 사실적인 이미지를 생성하는 것이 목적이다. 반면, 컴퓨터 비전에서는 실제 카메라의 특성을 모델링해 2D 이미지에서 3D 정보를 추출하는 데 중점을 둔다. 이를 통해 물체의 깊이, 위치 등을 계산하며, 스테레오 비전처럼 두 개의 이미지에서 3D 구조를 복원하는 역할을 한다. 기본적인 카메라 모델은 아래의 컴퓨터 그래픽스 페이지에 있고 이 페이지에서는 좀 더 2D - 3D 비젼 위주로 설명할 것이다.
Imaging Geometry

카메라로 촬영을 한다는 것은, 위와 같은 4개의 space을 모두 거친다는 의미이다. 즉, 4개의 좌표계 사이에 3번의 transformation이 발생한다. 우리가 카메라로 촬영한 이미지는 Pixel Coordinates 상의 (u, v) 좌표로 표현되는데 이러한 이미지의 2D 좌표는 실제 3D 공간에서의 정보를 투영(projection)한 결과이다. 이 과정을 Forward Projection이라고 하며, 카메라 모델을 통해 3D 공간의 점을 2D 이미지 평면으로 변환하는 작업이다. 그러나 컴퓨터 비전의 주요 과제는 이와 반대로, Backward Projection을 통해 2D 이미지로부터 3D 형상을 재구성하는 것이다. 즉, 스테레오 비전이나 모션 분석을 통해 여러 시점에서 얻은 이미지를 바탕으로, 원래의 3D 구조를 추정하는 작업을 수행해야 한다. 이를 위해서는 Forward Projection을 잘 이해하고, 이를 역으로 적용하여 3D 정보를 복원하는 것이 중요하다.
Forward Projection

- World Coords → Camera Coords: Rigid Transformation
- Cameara Coords → Film Coords: Perspective Transformation
- Film Coords → Pixel Coords: Affine Transformation
World Coordinates에서 Camera Coordinates로 변환하는 과정에서 (U, V, W) 좌표는 (X, Y, Z) 좌표로 변환되며, 이 과정에서 데이터의 크기나 모양에 왜곡이 발생하지 않는다. 이러한 변환을 Rigid Transformation이라고 하며, 이는 물체의 형태를 유지하면서 위치와 방향만을 변경하는 변환이다. Rigid Transformation은 회전(rotation)과 평행 이동(translation) 두 가지 변환으로 이루어지며, 이 과정에서 물체의 크기나 각도는 변하지 않고, 원래의 구조를 그대로 유지한다.

위는 rigid transformation하기 위한 행렬식이다. 먼저 가운데 행렬과 가장 오른쪽 행렬을 보면, 각각에 상수값을 더해주는 translation과정이라고 볼 수 있다. 그리고 왼쪽 행렬은 3차원 공간을 rotation하기 위한 matrix이다.
Pinhole Camera Model

3D 좌표를 2D로 변환할 때, z축 상의 모든 점은 2D 평면의 한 점에 모이게 된다. 이때, y / f = Y / Z라는 관계를 사용할 수 있는데 여기서 f는 카메라의 초점 거리(focal length)로 이미 주어진 값이며, y는 2D 이미지 평면에서의 좌표이다. 따라서 f와 y는 모두 주어진 값이다. 두 삼각형은 닮음 관계를 가지므로, 비례식을 통해 f= Z라는 비율을 알 수 있다. 이를 정리하면, 2D 좌표 y는 y = f * Y / Z로 표현되며, 이를 통해 3D 공간에서의 좌표를 2D 평면으로 투영할 수 있다.
Perspective Projection

x = f * X / Z, y = f * Y / Z는 비선형 방정식으로, 3D 공간에서 Z축 상의 모든 점들이 2D 이미지 상에서 동일한 한 픽셀에 매핑된다. 이는 광선 OP 상의 모든 점이 이미지 평면에서 같은 P 점으로 나타나는 근본적인 모호성으로, 3D에서 2D로 투영할 때 발생하는 정보 손실의 원인이다. 즉, Z축의 깊이 정보가 사라져 동일한 픽셀 안에 여러 3D 점이 포함되는 문제가 생기는 것이다.
Weak Perspective Approximation

물체와 카메라 간의 거리가 충분히 멀다면, 즉 Z값이 매우 크다면 카메라를 좌우로 움직여도 물체의 모습이 크게 변하지 않는다. 이때 좌우 이동에 따른 Z값의 변화를 무시하고 Z를 상수로 가정하는 것이 weak perspective 모델이다. 물체가 멀리 있을 때 깊이 변화를 무시하고 단순화된 투영 방식을 사용하여 3D 물체를 2D 이미지로 변환하는데, 이를 통해 계산이 간단해지며, 특히 원근감이 약해진 경우에 유효한 근사 모델이다.

센서가 좌우로 늘어져 있을 경우, 촬영된 이미지는 원래의 비율보다 홀쭉하게 왜곡되어 나타난다. 이러한 왜곡을 Deformation이라고 하며, 이는 카메라와 이미지 간의 관계에서 발생하는 현상이다. 이 과정에서 Affine transformation이 중요한 역할을 하는데, Affine transformation은 점, 직선, 평면 등의 기하학적 구조를 변형시키는 수학적 방법으로 크기나 형태를 왜곡하지 않으면서도 위치를 이동하거나 회전, 비율을 조정할 수 있는 변환이다. 따라서 카메라의 센서가 비정상적으로 배열될 경우, 이 affine transformation을 통해 이미지의 픽셀을 왜곡시킨다.
센서를 직사각형으로 만드는 주된 이유는 다양한 비율의 이미지와 호환성을 높이기 위함이다. 정사각형 센서는 특정 비율의 이미지를 촬영할 때 변형(deformation)이 발생하지 않을 수 있지만, 현실에서는 다양한 장면과 객체가 존재하여 여러 비율의 이미지에 대해 균일한 촬영을 보장하기 어렵다. 직사각형 센서는 특정 화면 비율(예: 16:9, 4:3 등)에 최적화되어 있어 영화, TV, 스마트폰 등 다양한 매체에 맞는 영상 촬영에 유리하며, 더 넓은 필드 오브 뷰를 제공하여 다양한 환경에서 활용 가능성이 높아진다. 따라서 직사각형 센서는 다양한 촬영 조건과 응용 분야를 고려했을 때 더 실용적이고 유연한 선택이 된다.
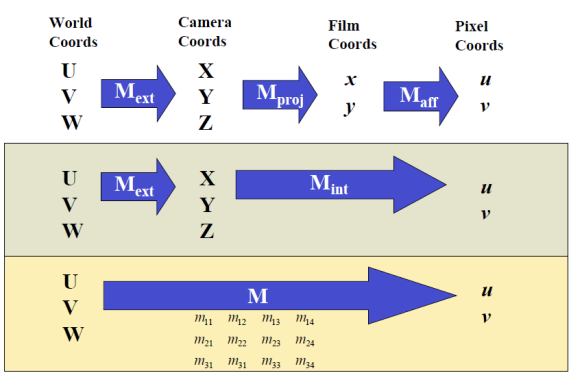
World Coordinates에서 Camera Coordinates로 변환되는 과정을 External Transformation이라고 하며, 이는 카메라 외부에서 발생하는 변환을 의미한다. 이와 달리, 카메라 내부에서 일어나는 변환은 perspective transformation과 affine transformation을 포함하여 Internal Transformation이라고 부른다. World Coordinates와 Camera Coordinates 사이에는 시점의 이동만 존재하지만, World Coordinates가 필요한 이유는 여러 대의 카메라가 있을 때 각 카메라의 기준이 아닌 하나의 통일된 기준을 제공하기 때문이다. 이는 서로 다른 카메라 간의 상대적 위치와 방향을 이해하고, 특정 카메라를 기준점으로 삼아 3D 공간의 객체를 보다 효율적으로 처리할 수 있게 해준다.
Consider a Line in the World.
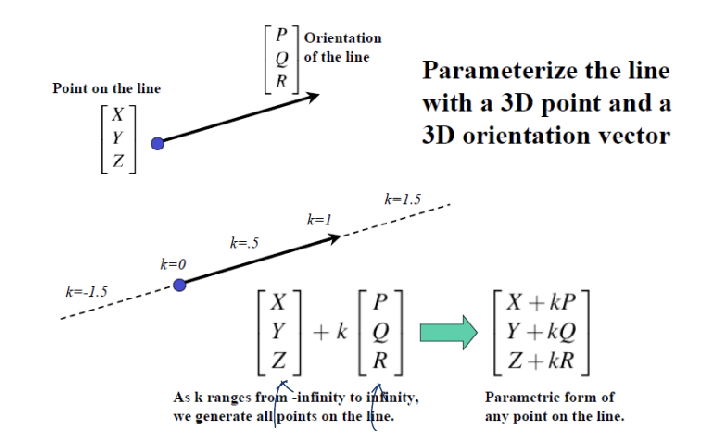
[X, Y, Z]'는 점을 의미하고, [P, Q, R]'은 벡터를 의미한다. 이 두 벡터를 더한다는 의미는, 하나의 point에서 어떤 방향(벡터)으로 갈건데, k만큼 이동하겠다는 것을 의미한다. 이렇게 계산된 결과인 [X + kP, Y + kQ, Z + kR]은 3차원 공간 상의 선을 의미한다.
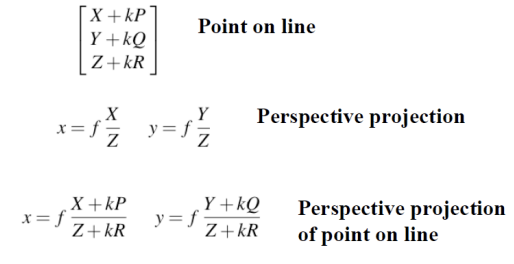
이렇게 계산해보면 다음과 같은 결과가 나온다.
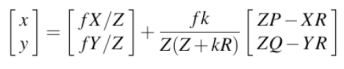
결과적으로, [x,y]는 2차원 상에서의 '선'을 의미하게 된다. 이는 3차원 공간에서의 선을 2차원으로 변환하더라도 여전히 선의 형태를 유지한다는 것을 나타내는데 3D 공간에서의 점과 방향을 기반으로 계산된 결과가 2D 평면에 투영되면, 선은 그 투영된 형태로 나타나며 이 과정에서 선의 기하학적 특성은 변하지 않는다. 따라서 3D 선을 2D로 변환하더라도, 그 결과가 선으로 유지된다는 것은 3차원과 2차원 간의 관계에서 중요한 성질이다.
Camera Projection Equation
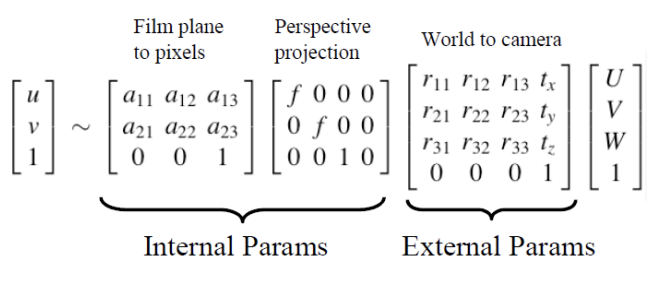
주어진 (u,v)좌표에서 등호(=)가 아닌 비례 기호(~)가 사용되는 이유는, 프로젝션 과정에서 발생하는 정보 손실 때문에 크기 정보를 정확히 담지 못하고 비례 관계를 갖기 때문이다.
Stereo
스테레오 비전에서는 두 대 이상의 카메라를 사용하여 동시에 동일한 대상을 촬영할 수 있으며, 이를 통해 두 이미지 간의 차이를 분석하여 깊이 정보를 추론할 수 있습니다. 이러한 방식은 3D 공간에서의 위치와 형태를 보다 정밀하게 재구성하는 데 중요한 역할을 한다.
Fundamental Ambiguity
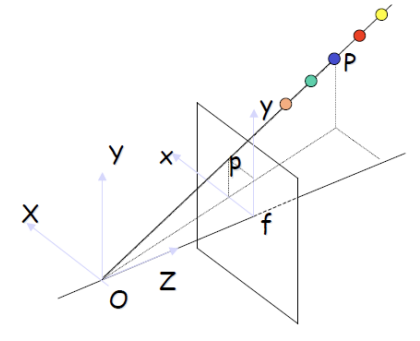
주어진 식에서 x=f∗X/Z를 보면, 깊이 Z값이 변화하더라도 k라는 상수를 곱하여 비례 관계를 유지할 수 있다. 즉, x=f∗kX/kZ와 y=f∗kY/kZ와 같이 표현될 수 있다. 이는 거리가 멀어지거나 가까워질 때, Z축 기준으로 동일한 선상에 있는 여러 점들이 동일한 2D 픽셀 위치에 매핑된다는 것을 의미한다. 결과적으로, 깊이에 따라 수없이 많은 (X,Z) 또는 (Y,Z)세트가 동일한 2D 좌표에 대응하게 되며, 이는 특정 3D 장면에서 여러 물체가 같은 픽셀에 투영될 수 있다는 모호성을 초래한다. 이 때문에 카메라는 깊이 정보 없이 3D 객체를 정확히 구분하기 어려워지며, 이는 3D 복원 및 깊이 추정 과정에서 중요한 고려 사항이 된다.
Recovering Depth Information
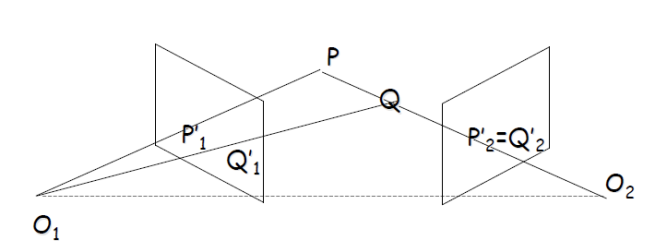
두 개의 카메라를 사용하여 깊이 정보를 회복할 수 있는 이유는 두 카메라 간의 거리와 각 카메라가 촬영한 이미지에서 물체의 위치 차이를 활용하는 것이다. 왼쪽 카메라에서 물체 P와 Q는 서로 다른 픽셀에 위치하지만, 오른쪽 카메라에서는 동일한 선상에 있어 하나의 픽셀에 찍힌다. 이 정보를 바탕으로 카메라 간의 거리와 물체의 위치 변화를 이용해 삼각형을 형성하면, 삼각법을 통해 물체가 카메라로부터 얼마나 떨어져 있는지를 계산할 수 있다.
A Hitchhiker's Guid to Parallax

두 개의 카메라로 동시에 촬영한 두 이미지를 비교하면 가까이 있는 물체는 큰 움직임을 보이고 멀리 있는 물체는 상대적으로 작은 움직임을 보이는데 이는 깊이 정보와 비례하는 관계를 나타낸다. 이러한 움직임의 차이를 수치화할 수 있으며 이를 통해 가까운 물체일수록 더 많이 움직이고 먼 물체는 덜 움직인다는 결론을 이끌어낼 수 있다. 깊이 정보를 측정하는 방식에는 두 가지가 있는데 DENSE 방법은 모든 픽셀에서 거리 정보를 측정하여 형상 정보를 얻지만 정밀도가 떨어지고 SPARSE 방법은 특정 물체에 대해서만 측정하여 정밀도는 높지만 제한적이다. 두 이미지는 동적이지 않고 정적이어야 하며 동일한 카메라로 동시에 촬영해야 한다. 그러나 삼각법을 적용하기 위해서는 카메라 간의 거리를 정확하게 측정하고, 두 이미지에서 물체가 동일한 것인지 확인할 수 있는 방법, 즉 매칭 문제를 해결해야 하는 어려움이 있다.
Dense - 이미지의 모든 픽셀에서 깊이 정보를 계산하여 전체 형상 정보를 얻는 접근 방식이다. 일반적으로 스테레오 비전이나 구조광 기술을 통해 밀집된 깊이 맵을 생성하며, 이를 통해 복잡한 지형이나 객체의 전체 형태를 재구성하는 데 유리하다. 그러나 전체 장면에 대한 연속적인 깊이 정보를 제공하는 만큼 계산량이 많아 처리 속도가 느리고 저조도 환경에서는 정밀도가 떨어질 수 있는 단점이 있다. 예를 들어 LiDAR 센서는 특정 지역의 모든 픽셀에 대해 거리 정보를 측정하여 3D 포인트 클라우드를 생성한다.
Sparse - 특정 물체나 관심 영역에 대해서만 깊이 정보를 측정하는 접근 방식으로 주로 특징점 추출 및 매칭을 통해 형상 정보를 얻는다. 이 방법은 특정 객체에 대해 매우 정밀한 정보를 제공하며, 계산량이 적어 속도가 빠르다는 장점이 있지만 측정된 영역이 제한적이기 때문에 전체 장면에 대한 정보는 부족한 단점이 있다. 예를 들어, SIFT(Scale-Invariant Feature Transform) 알고리즘은 이미지에서 고유한 특징점을 찾아내어 이들 간의 관계를 분석하여 특정 물체의 3D 모델을 생성할 수 있다.
A Simple Stereo System
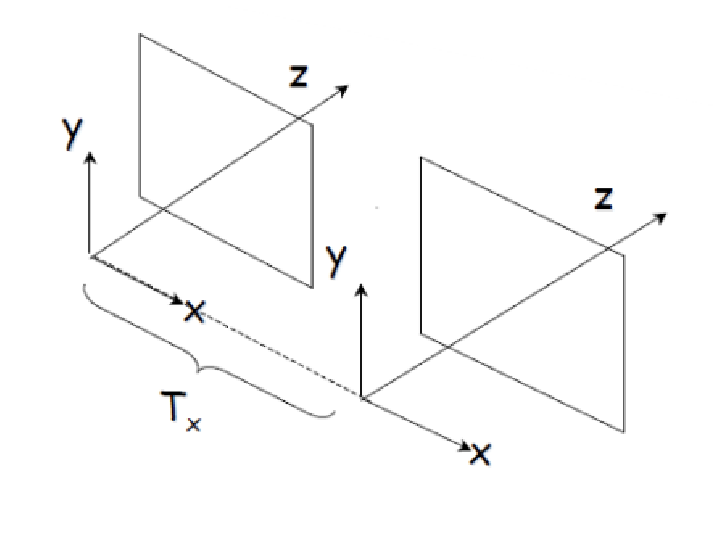
스테레오 카메라 설정에서는 두 카메라의 초점 거리 f1과 f2가 동일한 f로 설정되며 어파인 내부 매개변수 행렬 A1과 A2도 동일한 행렬 를 사용하여 두 카메라가 동일한 모델임을 가정한다. 외부 매개변수에서는 카메라 간의 변환을 나타내는 회전 행렬 을 단위 행렬 로 설정하여 회전이 없음을 나타내고, 평행 이동 벡터 는 (T′x,0,0)로 설정하여 x 방향(좌우)으로만 이동함을 정의한다. 이 구성은 3D 재구성이나 깊이 추정을 위한 기본적인 스테레오 비전 시스템을 형성한다.
A simple Stereo System-Top Down View (XZ plane)
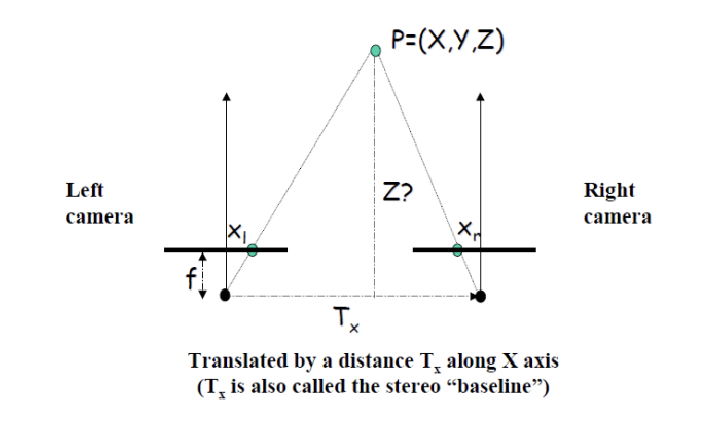
두 카메라 사이의 거리를 T′x라고 하며, 이를 baseline이라고 부른다. 두 카메라에서 동일한 위치에 있는 물체를 촬영한 이미지를 서로 겹치게(overlap) 하면, 물체의 이미지가 두 카메라에서 각각 다른 위치에 찍히게 된다. 이때 두 카메라에 찍힌 픽셀 사이의 거리를 parallax distance라고 하며, 이는 물체의 깊이 정보를 추정하는 데 중요한 역할을 한다. Parallax distance는 두 카메라의 시점 차이에 의해 발생하는 차이로 물체의 3D 위치를 계산하는 데 사용된다.

Projection Equation
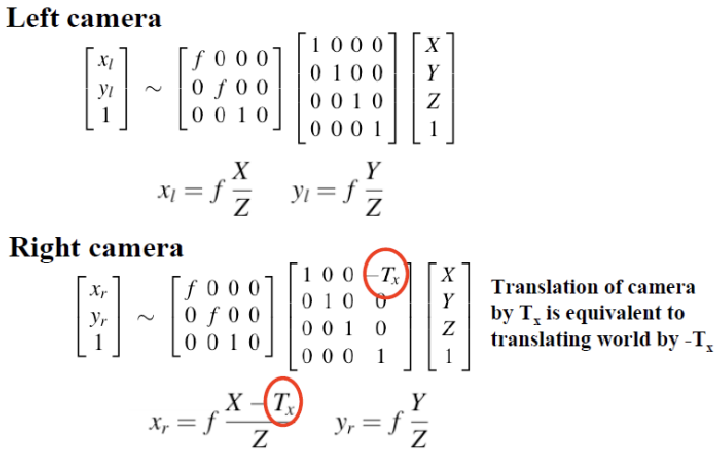
왼쪽 카메라에서 월드 좌표를 카메라 좌표로 변환할 때, 아무런 변환을 적용하지 않음으로써 왼쪽 카메라를 월드 좌표계로 정의하는 것이다. 반면 오른쪽 카메라는 왼쪽 카메라 좌표계와 일치시키기 위해 x 방향으로만 평행 이동(translational transformation)을 적용하여 변환 행렬이 생성된다. 이렇게 함으로써 두 카메라의 좌표계를 정렬하여 3D 재구성에 필요한 일관성을 유지할 수 있다.
Stereo Disparity
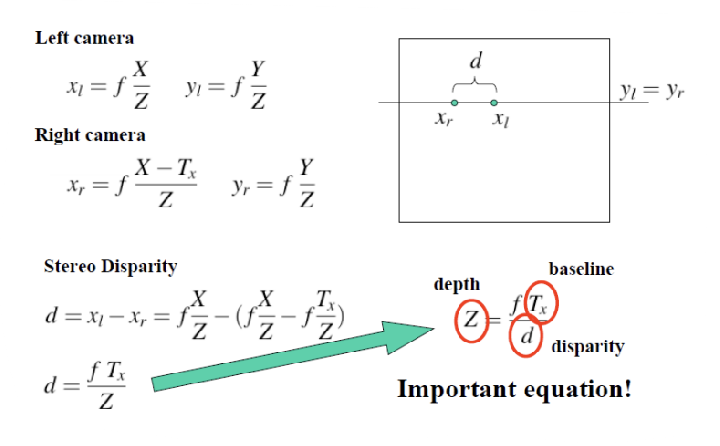
Disparity 는 오른쪽 카메라의 픽셀 x′r과 왼쪽 카메라의 픽셀 x′l간의 차이를 나타내며, 이 값이 클수록 카메라로부터 물체까지의 거리가 가까움을 의미하고, 반대로 작을수록 거리가 멀다는 것을 나타낸다. 두 카메라 사이의 거리인 baseline T′x와 깊이 Z는 다음과 같은 관계식 Z=f⋅T′xd로 연결되며, 여기서 깊이와 스테레오 disparity는 반비례 관계에 있다는 점이 중요하다. 또한, 대응 매칭(correspondence matching)을 수행할 때 사용할 수 있는 측정 방법으로는 유사도(similarity)와 차이성(dissimilarity) 지표인 SSD(Sum of Squared Differences)가 있다.
Stereo Example
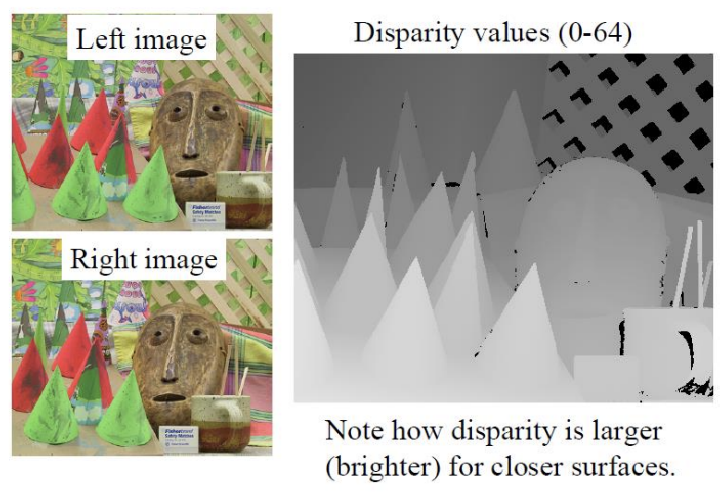
물체가 가까울수록 밝기가 밝아지고, disparity가 클수록 물체가 가까워진다는 관계가 성립하므로 disparity의 역수를 취하면 depth 값을 얻을 수 있다. 하지만 몇 가지 이상한 점이 있는데 첫째, 오른쪽 이미지에서 보이지 않는 영역까지 disparity 값이 계산되어 있고 둘째, 검은색 부분은 일치하는 패치를 찾지 못했음을 나타낸다. 패치를 이용한 correspondence matching 과정에서 물체의 edge 부분에서는 배경 변화가 크기 때문에 8-이웃(neighbor)의 값이 달라지는 문제가 발생한다. 이로 인해 edge 주변에서 disparity 값이 불규칙하게 나타나게 되며, disparity 값이 깔끔하게 나오기 어려운 상황이다.
Recall: Simple Stereo System
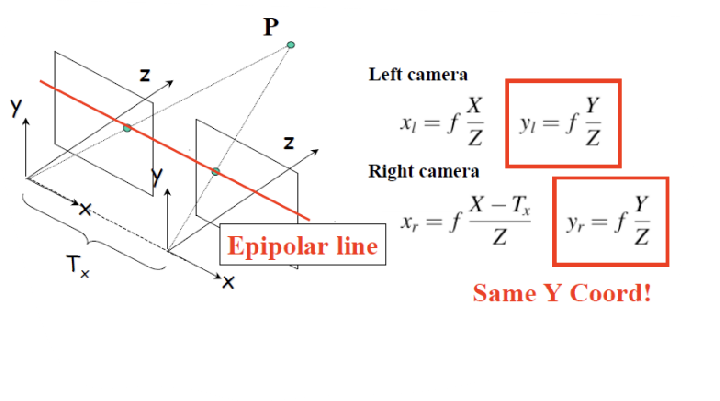
Epipolar Line은 두 카메라에서 동일한 물체가 찍힌 픽셀 포인트를 연결하는 선을 의미한다. x 방향으로만 평행 이동했기 때문에, 이 선을 따라 y값은 동일하게 유지된다. 즉, 특정 픽셀의 disparity를 활용하여 왼쪽 카메라의 픽셀과 대응되는 오른쪽 카메라의 픽셀은 같은 y좌표를 가지며, 이를 통해 3D Reconstruction을 위한 매칭 과정에서의 효율성을 높일 수 있다.
Matching using Epipolar Lines
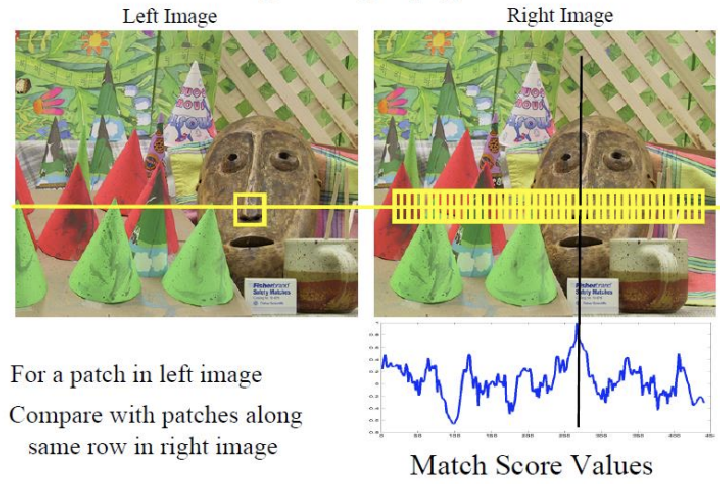
Epipolar Line을 활용하여 전체를 탐색(full search)하는 대신, 왼쪽 이미지의 패치와 일치하는 부분을 오른쪽 이미지에서 찾는 방식을 사용할 수 있다. 왼쪽 이미지를 기준으로 오른쪽 이미지는 물체가 왼쪽으로 이동한 것처럼 보이므로, 패치의 왼쪽 부분만 살펴보면 된다. 또한, 모든 영역을 검토할 필요는 없으며, 두 카메라 사이의 baseline T′x범위 내에서만 확인하면 된다. 이렇게 하면, 해당 범위 내에서 disparity에 따라 물체와의 관계를 잘 유지하며, 빠르고 효율적으로 대응점을 찾을 수 있습니다. 이 방식은 계산량을 줄이고 정확한 매칭을 도와준다.
Example: 5x5 windows NCC match score

Correspondence matching은 시점에 따라 픽셀 값이 일정해야 한다는 전제에 기반한다. 그러나 시점이 달라지면 조명 변화, 반사, 또는 가려짐 등으로 인해 픽셀 값이 변할 수 있으며, 이는 매칭 실패로 이어진다. 특히, patch 기반 8-neighbor 비교 방식에서는 픽셀 값이 다르면 정확한 대응을 찾기 어렵다. 이러한 문제는 edge 부근에서 자주 발생하며, 이를 근본적으로 해결하지 않으면 correspondence matching이 실패하게 된다.
픽셀 값이 유지된다는 가정은 correspondence matching에서 두 시점의 이미지를 비교할 때 동일한 물체의 같은 지점을 찾기 위한 기준이기 때문이다. 즉, 한 시점에서 본 픽셀과 다른 시점에서 본 픽셀이 같다면, 그 두 픽셀이 같은 물체의 동일한 지점을 나타낸다고 가정할 수 있다. 이를 통해 두 이미지 간의 대응점을 찾아 물체의 깊이 정보를 계산하는 등 3D 재구성을 수행할 수 있다. 만약 픽셀 값이 유지되지 않으면, 같은 물체라도 각 시점에서 다른 값으로 나타나므로 매칭이 어려워진다. 예를 들어, 조명 변화로 인해 한 시점에서는 밝고 다른 시점에서는 어두운 픽셀이 나타나면, 동일한 지점을 서로 다른 곳으로 잘못 매칭할 가능성이 커진다. 따라서 픽셀 값이 일정하다는 가정은 정확한 대응점을 찾기 위한 핵심 요소이다.

Correspondence matching 문제를 완화하기 위해 kernel의 크기를 키우면 좁은 영역에서 발생하는 노이즈에 덜 민감해지지만, 그만큼 이미지의 세부 정보가 손실되고 부드럽게 표현된다. 이를 통해 global optima에 가까운 지점으로 이동할 가능성은 높아지지만, 정확한 매칭은 여전히 어려울 수 있다. 특히 flat한 영역, 전반사 또는 uniform 반사와 같은 표면에서는 여전히 매칭 지점을 찾기 힘들며, 이런 경우는 대응점을 찾는 데 큰 어려움이 있다. 반면, texture가 많은 표면에서는 더 나은 매칭을 기대할 수 있다.
Correspondence matching 문제를 완화하기 위해 사용하는 커널(kernel)은 이미지의 특정 영역을 분석할 때 사용하는 작은 윈도우나 필터이다. 커널의 크기를 키우면 더 넓은 영역을 살피게 되어, 좁은 영역에서 발생하는 노이즈에 덜 민감해진다. 예를 들어, 작은 커널로 보면 이미지의 세부적인 패턴이나 노이즈에 민감하게 반응하지만, 큰 커널을 사용하면 노이즈가 상대적으로 줄어들고 전반적으로 부드러운 결과를 얻을 수 있다. 그러나 커널이 커지면 이미지의 세밀한 정보를 잃을 수 있으며, global optima(최적의 매칭 지점)에 가까워지는 가능성은 높아지지만, 그 지점이 정확하지 않을 수 있는 것이다.
예시: 작은 커널을 사용할 때는 나뭇잎의 디테일한 무늬까지 잘 잡히지만, 노이즈로 인해 오히려 매칭이 잘못될 가능성이 크다. 반대로 큰 커널을 사용하면 나뭇잎의 디테일이 흐려지지만, 나무 전체의 윤곽을 보고 매칭할 가능성이 높아진다. 그러나, flat한 영역(예: 하늘), 전반사(예: 유리 표면), 또는 uniform 반사(예: 벽과 같은 Lambertian surface)에서는 매칭이 어려운데, 이는 해당 영역들이 고유한 특징을 제공하지 않기 때문이다. 반면, 나무 껍질처럼 texture가 많은 표면에서는 커널 크기에 상관없이 비교적 쉽게 대응점을 찾을 수 있다.
Matching using Epipolar Lines
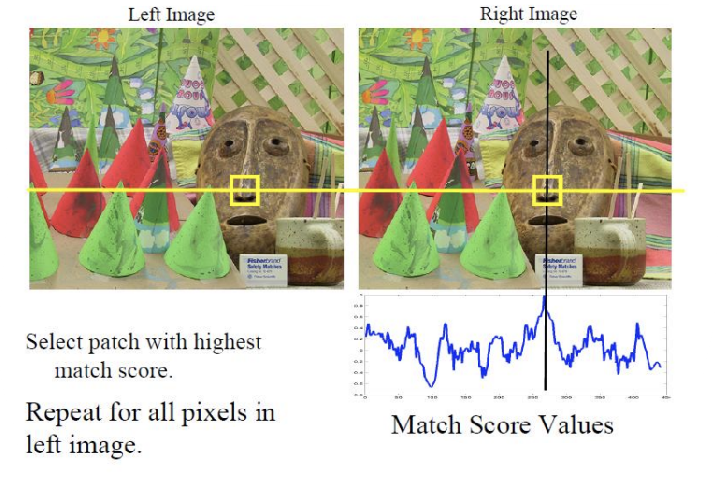
이전 시간에 배운 물체의 depth를 파악하는 과정은 두 단계로 이루어진다. 첫 번째로, 두 시점에서 동일한 물체의 일치하는 지점(correspondence point)을 찾는 것이고, 두 번째로 그 지점을 바탕으로 disparity 값을 계산하여 물체까지의 거리를 추정하는 것이다. 이제 남은 과제는 이러한 일치하는 지점을 정확하게 찾아내는 correspondence matching 문제를 해결하는 것이다.
Correspondence point를 찾는 문제는 독립적이지 않다. 카메라가 translation된 상태에서는 보이는 영역과 안 보이는 영역이 대부분 연속적이기 때문에, 모든 pixel pair가 독립적으로 매칭되지 않는다. 예를 들어, 7과 8 픽셀이 매칭되었다면, 그 다음 픽셀도 카메라의 translation을 고려하여 가까운 곳에서 매칭될 확률이 높다. 이를 통해 연속적인 픽셀 매칭을 쉽게 결정할 수 있지만, 처음 매칭이 잘못되면 그 뒤 픽셀까지 잘못 매칭되어 에러가 커진다. 이를 해결하기 위해 우리는 Inter-Scanline Consistency를 도입하여 동일한 scanline에서의 매칭 일관성을 확보하려고 한다. Disparity Space Image(DSI)는 left와 right 이미지의 한 row를 따라 patch를 이동하며 pairwise match scores를 계산한 것이다.
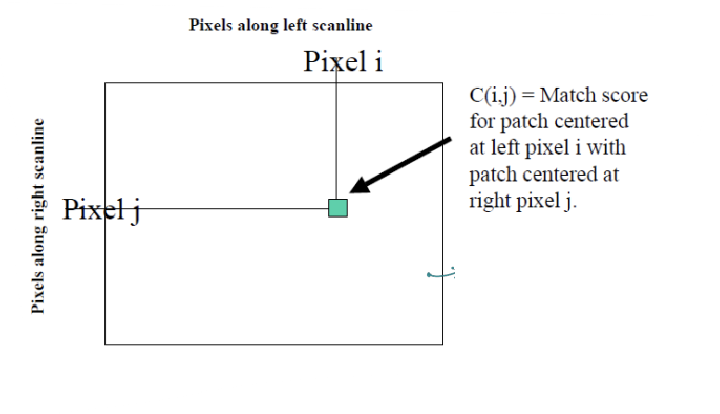
두 이미지의 하나의 row에 대해 각 인덱스별로 similarity를 구한 것이다.
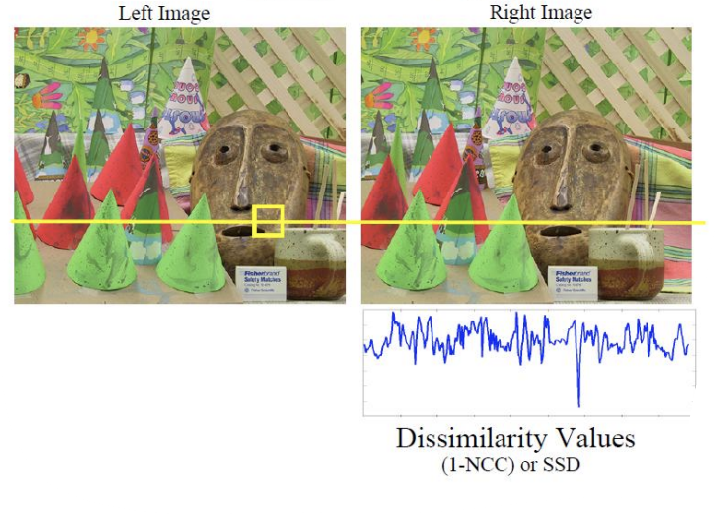
위 그림은 left image의 하나의 patch에 대해 right image에서의 dissimilarity(SSD)를 구한 것이다.
Disparity Space Image

DSI 이미지에서 left와 right 이미지가 바뀌었기 때문에, left 이미지의 10번 픽셀과 right 이미지의 7번 픽셀이 매칭됩니다. 이는 물체가 left 이미지에서는 오른쪽에 있지만, right 이미지에서는 왼쪽으로 이동한 형태로 나타나기 때문입니다. 따라서 (7, 10) 위치에서 dissimilarity 값이 가장 작아져 해당 픽셀들이 잘 매칭될 가능성이 높습니다. 이로 인해 DSI에서 최소값이 완벽한 대각선이 아닌, 약간 위쪽에 minimum line이 형성되며 매칭이 이루어집니다.
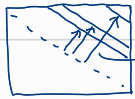
DSI에서 대각선에서 멀어질수록 카메라 두 대 사이의 거리가 멀어지는 것을 의미하며, 이는 baseline distance가 커짐을 나타냅니다. 그러나 정확하게는 baseline보다는 두 이미지 사이의 matching point 간의 disparity가 거리를 결정짓습니다. 즉, disparity가 클수록 두 카메라 사이의 거리가 더 멀어집니다. 이를 역으로 활용하면, DSI를 통해 baseline distance를 계산할 수 있지만, 이를 위해서는 픽셀 하나의 물리적인 크기를 알아야 합니다. 또한, DSI에서 나타나는 선이 항상 깔끔하지 않을 수 있는데, 이는 매칭 과정에서 발생하는 노이즈나 불완전한 대응 때문에 선이 왜곡되거나 불규칙하게 나타날 수 있기 때문입니다.
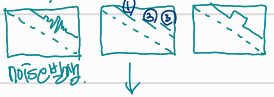
두 이미지에서 가장 가까이에 있는 물체는 3번입니다. 이는 두 이미지 사이의 disparity가 크기 때문에 대각선에서 멀리 떨어져 나타나며, 예를 들어 left 이미지의 50번 픽셀과 right 이미지의 2번 픽셀처럼 disparity가 크면 parallax에 의해 물체가 가까이 있음을 알 수 있습니다. 또한, DSI에서 보이는 검은색 큰 네모(즉, disparity 0인 영역)는 이동해도 변하지 않고 유사한 flat한 영역으로, foreground와 background의 급격한 변화로 인해 disparity가 텅 빈 것처럼 보이는 것입니다.
자, 이제 pixel은 continuous할 것이며, independent하지 않을 것임을 알았다. 그러면 이제 우리가 할 일은 optimal path를 찾는 일이다. path값들을 모두 더해서 minimum이 되는 값을 찾아보자.
Optimal path를 찾기 위해 DSI 전체를 다 볼 필요는 없습니다. 첫 번째로, 두 이미지의 이동을 분석하여 대각선 위와 아래 중에서 불필요한 영역을 버릴 수 있습니다. 이렇게 하면 검색할 영역이 반으로 줄어듭니다. 두 번째로, baseline을 알고 있으면 대각선에서 어느 정도 떨어진 영역까지만 확인하면 되므로, 탐색할 영역이 추가로 줄어듭니다. 이러한 두 가지 방법을 통해 전체 DSI를 고려하지 않고도 더 효율적으로 optimal path를 찾을 수 있습니다.
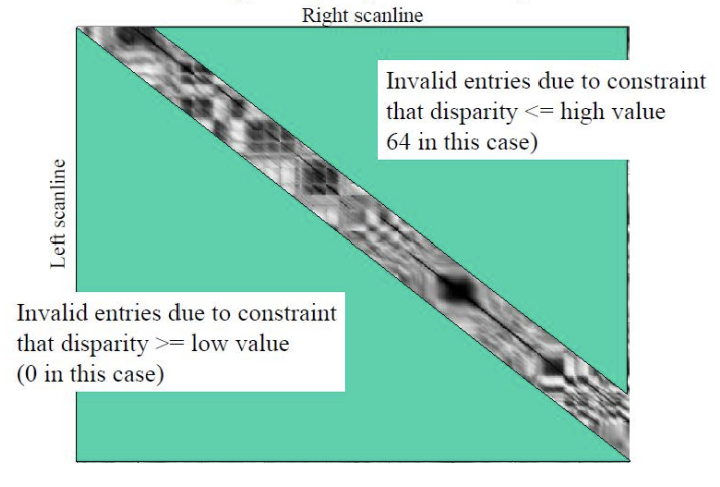
DSI and Scanline Consistency

100x100 이미지의 경우, 두 이미지에서 하나의 row만 고려하면 100x100 DSI가 생성됩니다. 이는 각 픽셀의 disparity 값을 계산하여 매칭 정보를 담고 있는 100개의 열과 100개의 행으로 구성된 매트릭스입니다. 만약 이미지를 full-search 방식으로 처리한다면, 모든 픽셀 쌍을 비교해야 하므로 100개의 DSI 이미지가 생성됩니다. 이는 각 픽셀에 대해 서로 다른 disparity 값을 계산하는 과정에서 발생하는 결과로, 이러한 방식은 계산량이 많고 비효율적일 수 있습니다.
Lowest Cost Path

"best" path를 찾기 위해서는 **lowest "cost"**를 목표로 해야 하며, 이는 path를 따라 dissimilarity의 합이 최소인 경로를 의미합니다. 이때, path에 대한 제약 조건으로는 double back하지 않음이 있습니다. 즉, 이미 지나간 픽셀로 되돌아가지 않아야 하며, 이는 경로가 효율적으로 진행되고 각 픽셀에 대한 일관된 매칭을 유지하는 데 도움을 줍니다. 이러한 제약을 통해 최적의 경로를 찾는 과정에서 계산의 복잡성을 줄이고 보다 정확한 결과를 도출할 수 있습니다.
Ordering Constraints
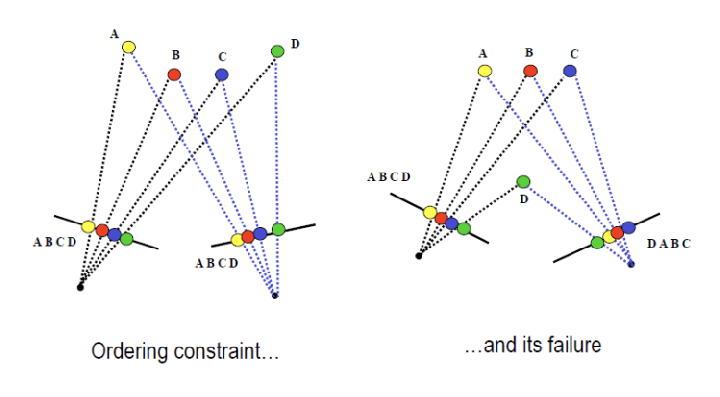
Dealing with Occlusions
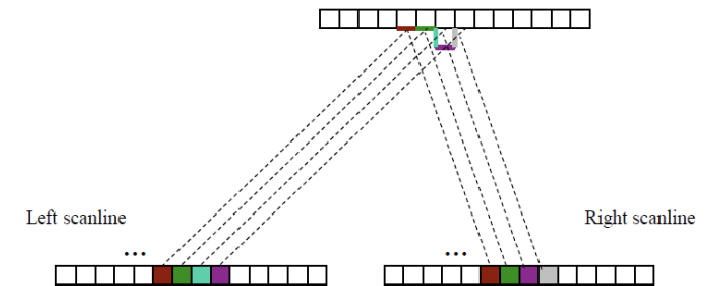
회색과 민트색같은 occlusion이 존재한다.
Occlusion은 3D 공간에서 하나의 물체가 다른 물체를 가려서 보이지 않게 되는 현상을 의미합니다. 이는 주로 시점이나 관찰 각도가 변경될 때 발생하며, 이미지 처리나 컴퓨터 비전에서 중요한 문제입니다. Occlusion은 두 이미지 간의 correspondence matching을 어렵게 만들어, 숨겨진 물체의 깊이 정보를 추정하거나 3D 재구성을 수행할 때 어려움을 초래합니다.
예를 들어, 한 장면에서 앞에 있는 나무가 뒤에 있는 건물을 가리고 있다면, 카메라가 나무를 통해 건물을 볼 수 없게 됩니다. 이 경우, 나무의 위치와 크기, 그리고 건물의 위치가 모두 영향을 받으므로 정확한 매칭 지점을 찾기 어려워집니다. Occlusion을 처리하기 위해 다양한 기법이 개발되고 있으며, 이를 통해 가려진 물체를 추정하거나 이미지의 불완전한 정보를 보완하는 방법이 연구되고 있습니다.
Search Over Correspondences
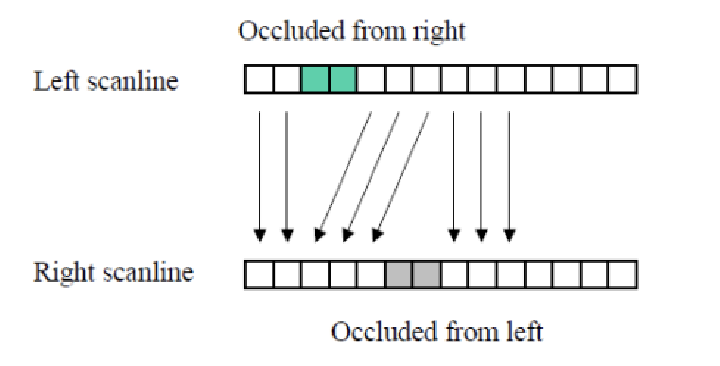
우리는 세 가지 경우를 고려할 수 있습니다. 첫 번째는 matching patches로, 이는 두 이미지에서 동일한 물체의 영역이 잘 매칭되는 경우를 의미합니다. 두 번째는 occluded from right로, 이는 오른쪽 이미지에서 왼쪽 이미지의 일부 물체가 가려져 보이지 않는 경우를 나타냅니다. 이 경우, 가려진 부분에 대한 대응점을 찾기 어렵고, 그로 인해 깊이 정보 추정이 복잡해집니다. 마지막으로, occluded from left는 왼쪽 이미지에서 오른쪽 이미지의 물체가 가려지는 경우로, 이 역시 동일하게 매칭 과정에서 문제를 일으킬 수 있습니다. 이러한 세 가지 경우는 각각 다른 방식으로 대응점을 찾는 데 도전 과제가 되며, occlusion 문제를 해결하는 데 중요한 고려사항이 됩니다.
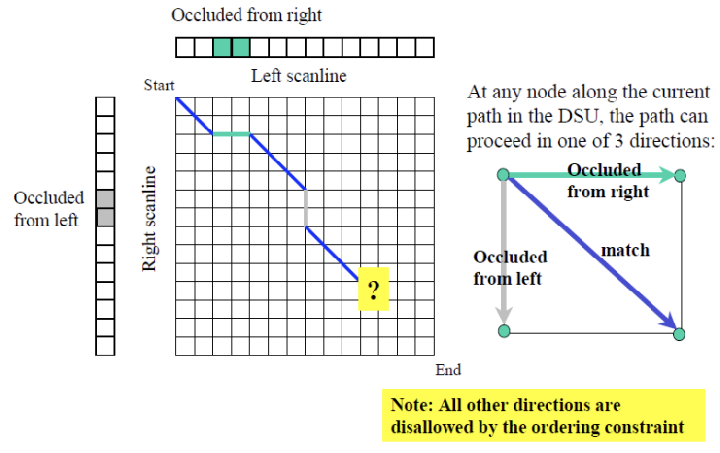
민트 색 영역은 오른쪽 이미지에서만 보이는 부분이며, 회색 영역은 왼쪽 이미지에서만 확인할 수 있는 부분입니다. 이러한 상황에서 ordering constraint를 고려하면, 위에서 언급한 세 가지 방향, 즉 매칭 패치, 오른쪽에서 가려진 경우, 왼쪽에서 가려진 경우만 가능하다는 것을 의미합니다. 다른 방향으로의 매칭은 불가능하며, 이는 각 이미지에서의 픽셀 순서와 깊이 관계가 충족되지 않기 때문입니다. 따라서 ordering constraint는 물체 간의 상대적 깊이와 위치를 유지하면서 올바른 대응점을 찾는 데 필수적인 요소가 됩니다.
각 path를 결정할 때마다 dissimilarity에 따라 방향을 선택합니다. 이 과정에서 dissimilarity가 높은 경우에는 왼쪽 occlusion인지 오른쪽 occlusion인지를 판단해야 합니다. 매칭 패치의 경우, Cost는 dissimilarity score로 설정되며, 이는 두 이미지 간의 유사성을 나타냅니다. 반면, 오른쪽에서 가려진 경우(occluded from right)에는 cost가 일정한 상수 값으로 설정되며, 이는 해당 영역이 가려져 있어 정확한 매칭이 어려움을 반영합니다. 왼쪽에서 가려진 경우(occluded from left) 역시 cost가 일정한 상수 값으로 처리되며, 마찬가지로 가려진 부분의 특성으로 인해 매칭에 대한 불확실성을 나타냅니다. 이러한 설정은 occlusion의 영향을 효과적으로 반영하여 경로 선택에 도움을 줍니다.
우리는 optimal path를 찾기 위해 Dynamic Programming 기법을 사용할 것입니다. 이 방법은 full-search처럼 모든 path를 일일이 살필 필요는 없지만, 각 픽셀의 가능성을 체계적으로 검토합니다. Dynamic Programming은 각 픽셀에 도달하기까지의 optimal score를 저장해두는 방식으로 작동하며, 실제로 path finding은 한 번만 수행됩니다. 이 과정에서 모든 픽셀의 가능성을 고려하여 값들을 저장함으로써, 나중에 경로를 추적할 때 최적의 결과를 빠르게 찾을 수 있도록 합니다. 이러한 방식은 계산 효율성을 높이고, occlusion과 같은 복잡한 상황에서도 효과적으로 대응할 수 있게 합니다.
'Camera & Vision > Computer Vision' 카테고리의 다른 글
| Vision Theory [5] : 영상 분할 (0) | 2024.11.07 |
|---|---|
| Vision Theory [4] : 이미지 매핑 (0) | 2024.10.28 |
| Vision Theory [2] : 에지 & 코너 검출 및 포인트 매칭 (2) | 2024.09.28 |
| Vision Theory [1] : 이미지의 정보와 처리 (3) | 2024.09.19 |
