
2D 이미지 한 장으로는 3D를 예측하기에 정보가 부족하므로, 두 장 이상의 이미지를 사용해 데이터 간 관계를 파악하는 것이 중요하다. 예를 들어, disparity 이미지를 통해 좌우 시점 기준의 두 개 depth를 얻어 서로 다른 시점 간 관계를 이해할 수 있다. 만약 다른 사람이 촬영한 두 장의 사진을 이용해 스테레오 시스템을 적용하고자 한다면 두 카메라 사이의 상호 관계를 알아야 한다. 이번 장에서는 주어진 두 이미지 간 변환 관계를 찾아내는 과정에 집중하여 기존 스테레오 시스템에서의 밀집한 대응점 찾기(dense correspondence)가 아닌, 확실한 희소 대응점(sparse correspondence)을 기반으로 두 카메라 간 이동 관계를 역으로 추정하고자 한다.
1. Image Mapping
Geometric Image Mappings
기준이 되는 이미지와 transformed된 이미지 사이의 관계를 파악하고자 한다.

Linear Transformation
기준이 되는 이미지와 변환된 이미지 간의 관계를 파악하려면, 두 이미지의 대응점을 통해 선형 변환을 찾는 것이 필요하다. 관측 데이터는 변환된 이미지의 점 좌표 [x′,y′,1]이고, 이는 기준 이미지의 점 좌표 [x,y,1]와 선형 변환 행렬 M을 통해 관계를 형성한다. 여기서 M은 변환을 설명하는 미지수(parameter)를 포함한 행렬로, 이 행렬의 각 요소는 회전, 이동, 축소, 확대와 같은 기하학적 변환을 나타낸다. 두 이미지 간의 관계를 추정하기 위해서는 여러 쌍의 대응점을 수집하고, 이 대응 관계로부터 의 파라미터를 계산하여 각 점이 변환될 위치를 추정할 수 있다. 이렇게 구한 을 통해 이미지 간의 기하학적 관계를 모델링할 수 있다.

Translation
2D 평면에서 두 이미지 간의 이동 변환(Translation)을 추정하려면, 변환 행렬(translation matrix)의 미지수는 두 개가 된다. 이 두 미지수는 와 방향의 이동 거리, 즉 각 축에 대한 이동량을 의미한다. 관측된 데이터와 기준 데이터의 대응점을 사용해 이 두 파라미터를 추정하면, 기준 이미지에서 변환된 이미지로의 이동 관계를 설명할 수 있다.

Estimating a Transformation

Example: Translation Estimation
이 예시에서는 translation 만 존재한다고 가정한다.

2D 이동 변환(Translation Transformation)에서는 자유도(DoF)가 두 개로, 와 방향의 이동량을 나타내는 미지수(parameter)가 각각 하나씩 존재한다. 따라서 필요한 최소 대응점(correspondence)도 1쌍이면 충분하다. 이 한 쌍의 대응점만으로도 tx와 ty 값을 해결할 수 있기 때문이다. 하지만 실제로는 여러 요인으로 인해 측정 오차가 발생하기 때문에, 하나의 대응점만으로는 신뢰성 있는 결과를 얻기 어렵다. 따라서 오류를 줄이기 위해 여러 대응점을 사용하여 추정의 정확도를 높인다.


이론적으로는 대응점(corresponding point) 한 쌍만 있으면 2D 이동 변환의 두 개 파라미터(tx, ty)를 구할 수 있지만, 실제로는 측정 오차와 같은 여러 오류가 존재하여 하나의 점만으로는 신뢰도가 낮다. 따라서 다수의 대응점을 사용하여 이러한 오류를 최소화해야 한다. 이를 위해 최소자승법(Least Squares Estimation)을 활용하는데, 여기서 오차(error)는 (이동전좌표+예측된이동파라미터) − 이동후좌표로 정의된다. 이 오차의 합을 최소화하기 위해 오차 함수를 tx와 ty에 대해 미분하여 극값을 찾고 이를 통해 오차가 최소가 되는 최적의 이동 파라미터를 구한다. 이를 통해 최적의 이동 변환을 추정하게 된다.

예를 들어, 기준 이미지에서 (xi,yi) 좌표를 가진 점이 이동 후 (xi′,yi′)로 변한다고 가정하자. 이 경우, 이동 변환에 의해 다음과 같은 관계가 성립한다
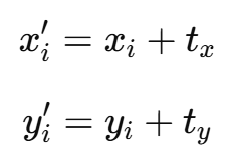
여기서 tx와 ty는 이동 변환의 파라미터이다. 이에 따라 오차(error)는 다음과 같이 정의할 수 있다.
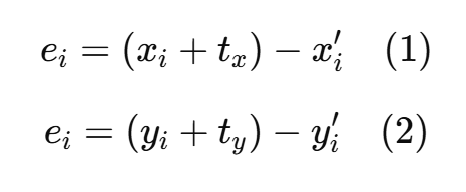
이 오차는 각 대응점에 대해 계산할 수 있으며, 전체 오차의 제곱합을 최소화하기 위해 다음과 같은 오차 함수를 정의할 수 있다.
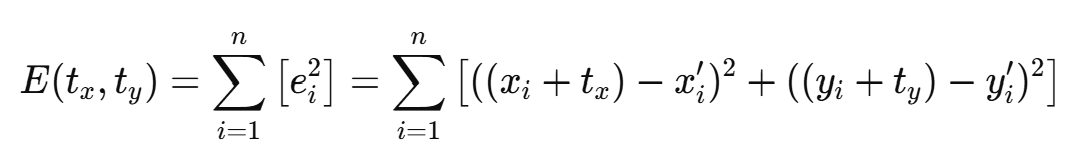
이 오차 함수 E를 tx와 ty에 대해 편미분하여 각 파라미터의 최적값을 구하는 방법은 다음과 같다:
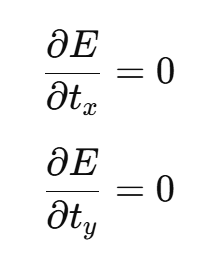
이 두 식을 풀면 최적의 이동 파라미터 tx와 ty를 얻을 수 있다. 예를 들어, 3개의 대응점이 다음과 같다고 가정하자:
- 기준 이미지: (1,2),(2,3),(3,4)
- 이동 후 이미지: (2,3),(3,5),(4,6)
이 경우 대응점에 대해 위의 공식을 적용하여 오차를 계산하고, 최소자승법을 통해 tx와 ty를 구할 수 있다. 이렇게 얻은 파라미터를 통해 최적의 이동 변환을 추정할 수 있다
Transformation Groups
어떤 변환 집합이 Transformation Group으로 불리기 위해서는 세 가지 조건을 만족해야 한다. 첫째, 두 변환을 연속으로 적용해도 그 결과가 동일 집합 내의 변환이어야 하고(폐쇄성), 둘째, 변환을 순차적으로 적용하는 순서가 결과에 영향을 미치지 않아야 하며(결합법칙), 셋째, 각 변환에 대해 원래 상태로 돌아가는 역변환이 존재해야 한다. 이러한 조건이 충족되면 해당 변환 집합은 그룹의 성질을 가지게 되어, 그 안에서 다양한 수학적 성질을 편리하게 활용할 수 있다. 이동(translation)과 회전(rotation) 변환은 이러한 조건을 충족하므로 Transformation Groups에 속하며, 이를 통해 공간 변환에서의 연산이 더욱 효율적으로 처리된다.

아래 사진처럼 우리는 손쉽게 inverse를 구할 수 있다.
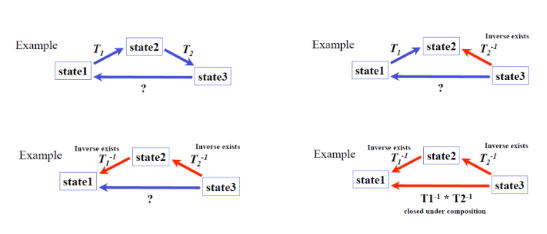
Basic set of 2D planar transformations
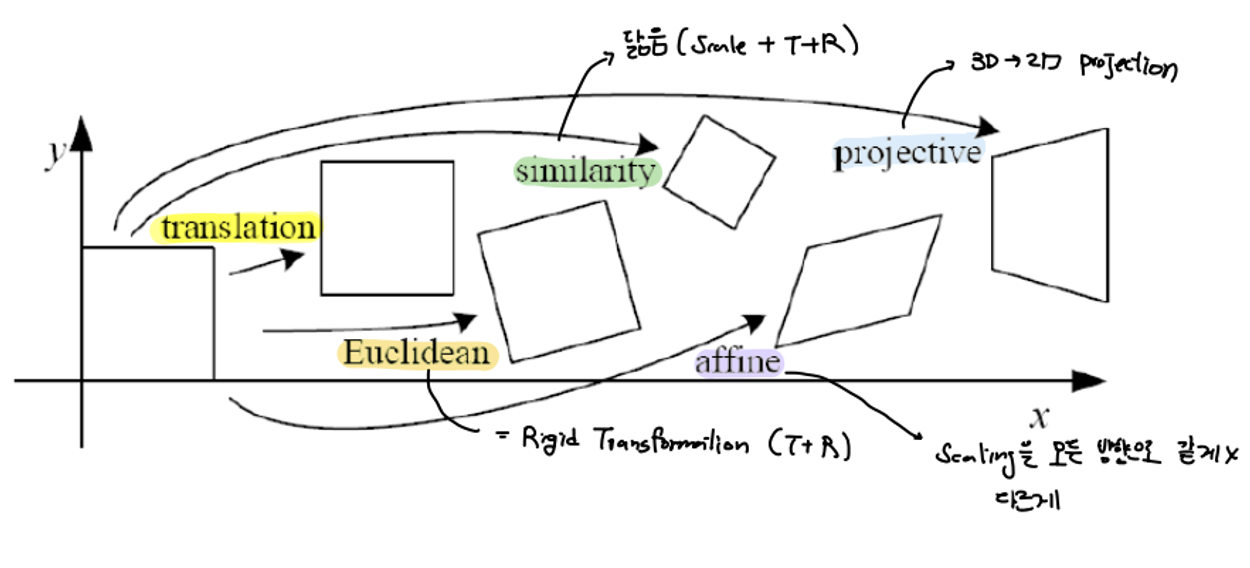
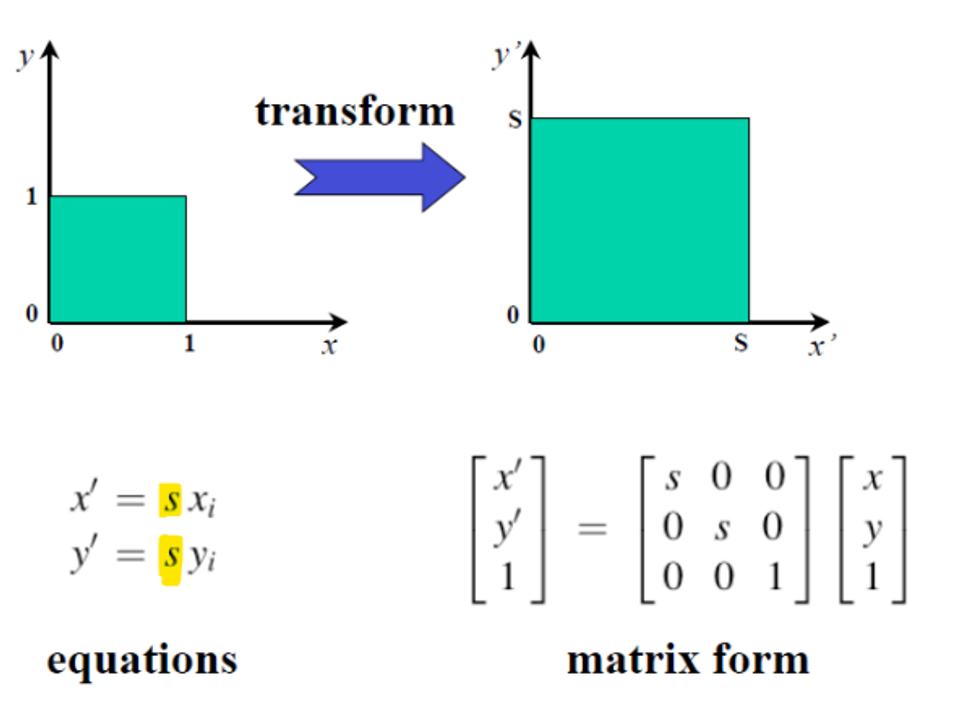
Scale
2D에서 하나의 스케일링(scaling) 파라미터 를 적용할 때, 자유도(DoF)는 1이며, 하나의 대응점(corresponding point)만으로도 ss를 추정할 수 있다. 그러나 s=0이면 객체가 사라지고, s가 음수일 경우 객체가 반전된다. 만약 객체가 원점에서 떨어져 있을 경우, 단순히 스케일링을 적용하면 원점으로부터의 위치까지 함께 변한다. 따라서 이러한 경우, 먼저 객체를 원점으로 이동(translation)시킨 뒤 스케일링을 적용하고, 다시 원래 위치로 이동(translation back)해야 한다. 이 과정에서 Transformation Group의 성질에 따라, 역변환(inverse)을 사용하여 마지막 복귀 단계를 간단히 수행할 수 있다.
Rotation
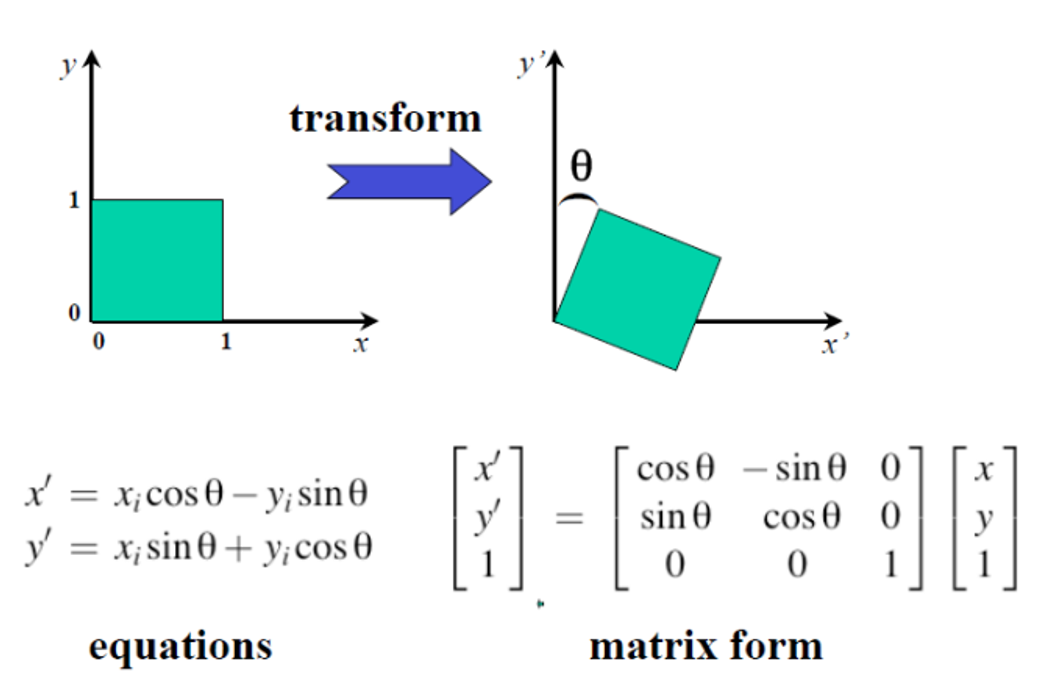
Euclidean
= Rigid Transformation = Translation + Rotation
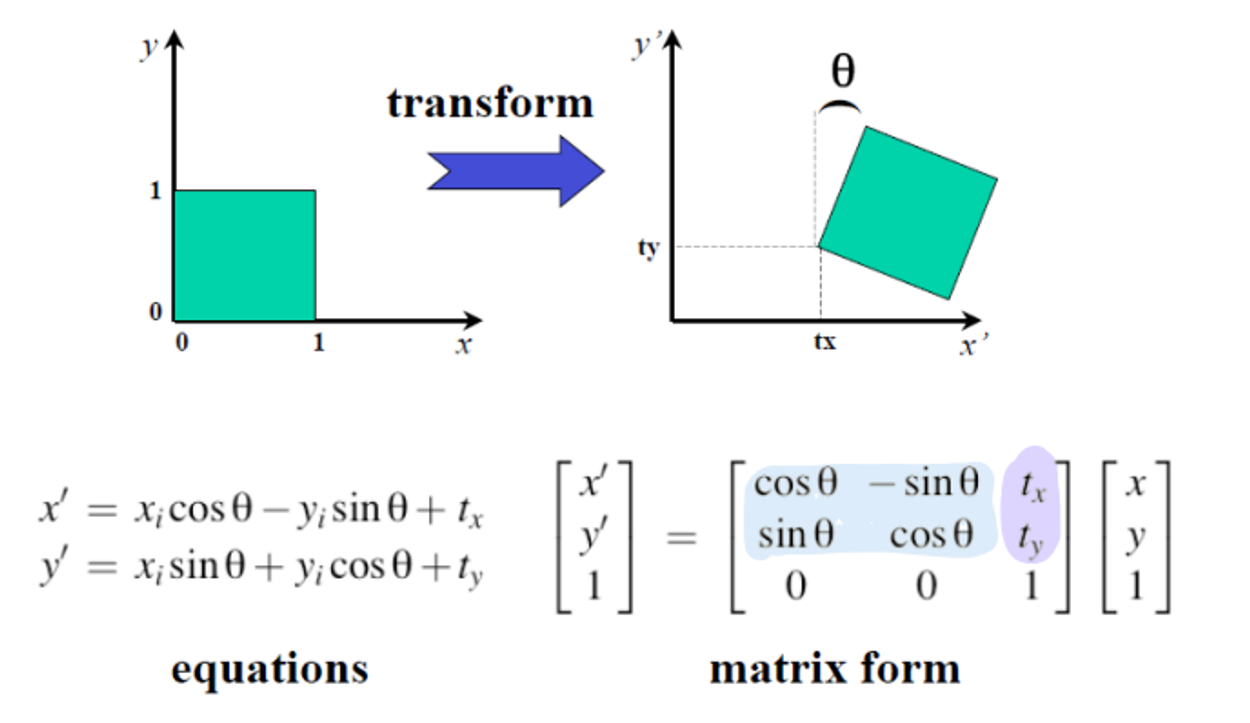
(Translation + Rotation) Matrix 를 아래처럼 표현하기도 한다.
- R : rotation matrix
- t : translation

Similarity
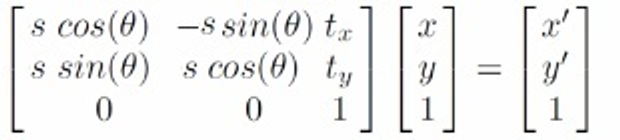
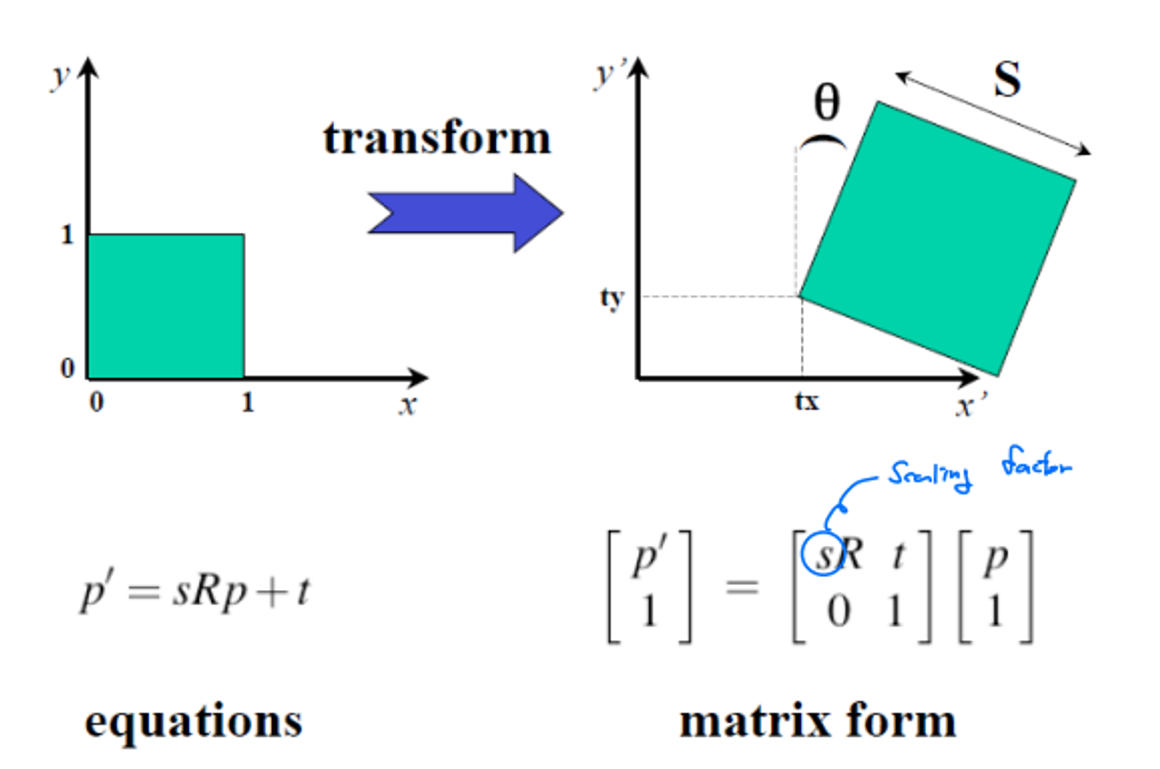
Scaled Euclidean Transform은 2D 공간에서 스케일링(Scaling), 이동(Translation), 회전(Rotation)을 포함하는 변환으로, 총 4개의 미지수 파라미터 tx, ty, s, θ를 가진다. 이를 구하기 위해서는 최소한 2개의 대응점(corresponding point)이 필요하며, 예를 들어 기준 이미지의 점 A(1,2)와 B(3,4)가 각각 변환 후 A′(2,3)와 B′(4,6)로 이동한다고 가정할 수 있다. 이 경우, 두 점에 대한 변환 관계를 설정하면 각 점의 위치 변화에 따른 두 개의 방정식을 얻을 수 있으며 이를 통해 모든 미지수 파라미터를 추정할 수 있다. 이러한 과정은 변환의 정확한 이해와 적용을 가능하게 하여 다양한 응용에 활용된다.

2. Estimating Homography
Homography는 서로 다른 카메라 시점에서의 점을 변환하는데 사용되는 수학적 기법이다. 이를 통해 카메라 A의 점을 카메라 B의 점으로 변환할 수 있으며, 이 과정을 수식으로 표현하면 다음과 같다:
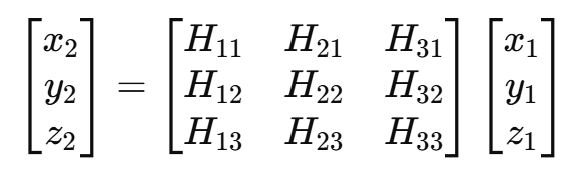
여기서 H는 Homography 행렬이고, x1,y1,z1는 카메라 A의 점, x2,y2,z2는 카메라 B의 점이다. 점들은 동차 좌표(homogeneous coordinates)로 표현되며, 실제 2D 좌표를 구하기 위해서는 x와 y를 z로 나누어야 한다. 동차 좌표를 비동차(inhomogeneous) 좌표로 변환하기 위해 z1=1로 설정하면 변환식은 다음과 같이 재작성될 수 있다.
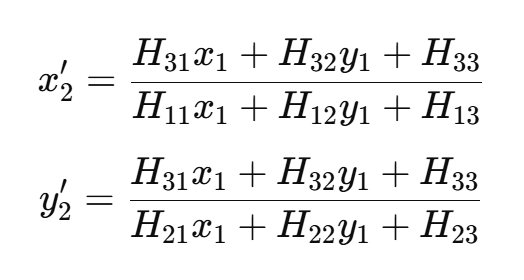
이러한 표현은 비동차 좌표계에서의 x2를 각 점의 변환으로 구하는 것을 보여준다
위의 두 방정식을 정리하면 Ah = 0 형태로 변환할 수 있다. 이는 다음과 같은 2n by 9 행렬 형태로 나타낼 수 있다:

여기서 n 쌍의 점을 이용하면 2n개의 방정식을 생성할 수 있으며 Homography 행렬은 8개의 자유도를 가진다. 따라서 최소 4쌍의 점이 필요하여 Homography를 계산할 수 있다.
3. 특징 추출과 모델 피팅
Random Sample Consensus (RANSAC)
선형 최소 제곱 추정(Linear Least Squares Estimation)은 주어진 데이터 포인트들에 대해 선형 모델을 적합시키는 방법으로, 주로 선형 관계를 가진 데이터에 적용된다. 이 방법은 초기 추정값이나 대략적인 솔루션을 제공하는 데 유용하지만 아웃라이어(outlier)에 대한 처리가 부족하다는 단점이 있다. 예를 들어, 데이터 포인트가 대부분 (1, 2), (2, 3), (3, 4)와 같은 선형 관계를 따르지만, 하나의 아웃라이어인 (10, 100)가 포함되어 있다고 가정해 보자. 이 경우 선형 최소 제곱 추정 방법은 아웃라이어의 영향을 받아 전체 데이터의 최적화된 선을 왜곡하게 되고 결과적으로 적합된 선형 모델이 실제 데이터의 경향을 잘 반영하지 못할 수 있다. 따라서 아웃라이어가 존재할 때는 보다 견고한 방법이나 사전 처리가 필요하다.

RANSAC(Random Sample Consensus)는 주어진 데이터셋에서 불규칙적인 데이터 포인트, 즉 outlier를 효과적으로 처리하기 위한 알고리즘이다. 이 알고리즘은 특정 모델을 데이터에 피팅하기 위해 무작위로 샘플을 선택하고, 이 샘플로부터 모델을 생성한 후, 전체 데이터 중에서 이 모델에 잘 맞는 인라이어(inlier)와 잘 맞지 않는 아웃라이어(outlier)를 분리한다. 이 과정을 반복하면서 모델이 가장 많은 인라이어를 가진 경우를 찾아내며, 최종적으로 선택된 인라이어를 기반으로 모델을 재추정한다. RANSAC은 특히 노이즈가 많거나 잘못된 매칭이 존재하는 환경에서 신뢰할 수 있는 매칭을 보장하는데 유용하다.
RANSAC의 주요 특징은 반복적이고 확률적인 접근 방식으로, 제한된 수의 샘플만으로도 강력한 모델을 구축할 수 있다는 점이다. 알고리즘은 먼저 랜덤하게 k개의 샘플을 선택하여 모델을 생성하고, 그 모델을 기반으로 모든 데이터 포인트에 대해 피팅 오류를 계산한다. 이 과정에서 주어진 임계값 이하의 오류를 가진 포인트들만을 인라이어로 간주한다. 이러한 방식으로 각 반복에서 생성된 모델의 인라이어 수를 세어 가장 많은 인라이어를 가진 모델을 선택하게 된다.

RANSAC을 이해하기 위해 간단한 선형 피팅(line fitting) 문제를 살펴보자. 예를 들어, 여러 개의 데이터 포인트가 주어졌다고 가정하자. 이 데이터 포인트 중 일부는 실제 선형 관계를 따르지 않고, 노이즈나 오류로 인해 산란되어 있는 아웃라이어(outlier)이다. 이러한 아웃라이어들이 포함된 데이터로 인해 우리가 기대하는 것과는 다른 편향(bias)이 있는 선형 모델이 도출될 가능성이 높다.
x축과 y축에 따라 분포된 데이터 포인트가 있다고 가정하자. 이 데이터의 대다수는 y = 2x + 1이라는 실제 선형 관계를 따른다고 하더라도 몇 개의 아웃라이어가 존재한다고 하자. 이 아웃라이어는 실제 선형 관계와는 전혀 다른 위치에 있어서, 이들을 포함하여 선형 회귀를 수행하게 되면, 구해진 직선은 아웃라이어의 영향을 받아 실제 선형 관계와는 크게 어긋나는 경향이 있다.
이 경우, 아웃라이어로 인해 구해진 선형 모델은 원래 데이터의 패턴을 잘 설명하지 못하게 되고, 실제로는 그다지 유용하지 않은 결과를 초래할 수 있다. 예를 들어, 아웃라이어가 포함된 데이터에 대한 최소 제곱법을 적용하면, 최적의 직선은 y 절편이 잘못 추정되거나 기울기가 실제보다 더 평행하게 나타날 수 있다. 이런 상황에서 RANSAC 알고리즘을 사용하면, 아웃라이어를 효과적으로 제거하고, 더 많은 인라이어를 기반으로 올바른 선형 모델을 추정할 수 있다. RANSAC은 반복적으로 데이터의 랜덤 샘플을 선택하고, 해당 샘플로부터 모델을 생성하여, 가장 많은 인라이어를 가진 모델을 찾는 방식으로 아웃라이어의 영향을 줄이는 데 효과적이다.

RANSAC 알고리즘에서 최적의 모델을 찾기 위해서는 무작위로 선택된 데이터 포인트들이 필요하다. 선형 모델을 피팅하기 위해서는 최소한 2개의 포인트가 선택되어야 한다. 이는 선형 방정식을 정의하기 위해 필요한 최소한의 정보로, 두 점을 통해 직선을 결정할 수 있기 때문이다. 알고리즘의 각 반복에서 RANSAC은 랜덤하게 2개의 포인트를 선택한 후, 이 두 점을 연결하는 직선을 정의한다. 이후 이 모델이 전체 데이터셋에 얼마나 잘 맞는지를 평가하기 위해, 모든 데이터 포인트에 대해 모델과의 거리 또는 오차를 계산한다. 이 과정에서 주어진 임계값 이하의 오차를 가진 포인트들을 인라이어로 분류하고, 모델을 재평가하여 가장 많은 인라이어를 가진 모델을 찾는다. 이러한 방법을 통해 RANSAC은 아웃라이어의 영향을 최소화하면서, 데이터의 주 패턴을 잘 나타내는 신뢰할 수 있는 모델을 구할 수 있게 된다.
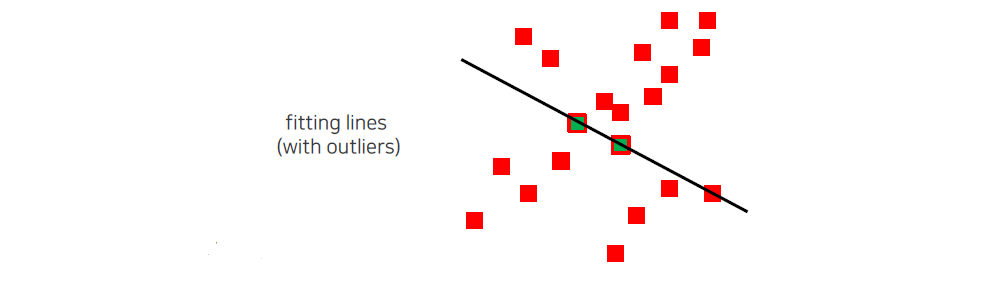
다음은 이렇게 구한 point들로 model parameter를 구하는 것이다. RANSAC은 계속해서 동일한 과정을 반복하기 때문에 간단한 solver를 사용할수록 좋다.
RANSAC 알고리즘에서 모델 파라미터를 구할 때는 각 반복에서 선택된 포인트들을 기반으로 간단한 솔버를 사용하는 것이 중요하다. 이는 RANSAC이 여러 번의 반복 과정을 거치면서 매번 무작위로 포인트를 선택하고 모델을 업데이트하기 때문에, 복잡한 계산을 요구하는 솔버는 성능을 저하시킬 수 있다. 예를 들어, 선형 피팅의 경우 두 점을 이용해 직선의 기울기와 절편을 쉽게 계산할 수 있는 직관적인 수학 공식을 사용할 수 있다. 이러한 간단한 솔버를 통해 빠르게 모델 파라미터를 추정할 수 있으며, 그 결과 RANSAC의 전체 수행 시간이 단축된다. 또한, 효율적인 솔버를 사용함으로써 RANSAC이 더 많은 반복을 수행할 수 있는 여유를 가지게 되어, 최적의 모델을 찾을 확률을 높이고 아웃라이어의 영향을 최소화할 수 있게 된다. 이처럼 RANSAC에서는 계산의 효율성을 고려하여 간단한 모델 파라미터 추정 방법을 선택하는 것이 중요한 전략이다.
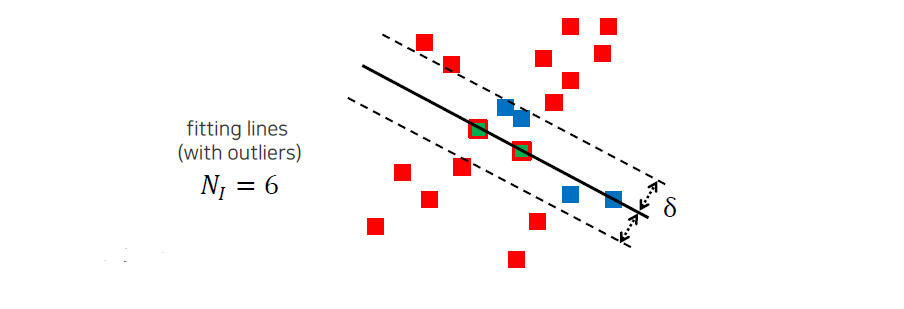
다음에는 이렇게 구한 line이 얼마나 좋은지 평가를 할 것이다. 라는 threshold bound를 주었을 때 이 경계를 기준으로 안에 있는 point들 inlier라 하고 밖에 있는 point들을 outlier라고 할 것이다. 여기서 는 사용자가 직접 정하는 것이고, inlier의 개수를 셀 것이다. 위에서는 6개가 inlier가 되기 때문에 이를 score로서 사용하게 될 것이다.
RANSAC 알고리즘에서 모델의 품질을 평가하기 위해, 사용자는 특정한 임계값인 δ(threshold bound)를 설정한다. 이 δ 값은 모델에 대한 오차의 허용 범위를 정의하며, 모델이 각 데이터 포인트와 얼마나 잘 맞는지를 판단하는 기준이 된다. 모델이 생성된 후, 각 데이터 포인트와 모델 간의 거리를 계산하여, 이 거리가 δ 이하인 포인트를 인라이어(inlier)로 분류하고, 그보다 큰 거리를 가진 포인트는 아웃라이어(outlier)로 간주한다. 이 과정에서 인라이어의 개수를 세는 것이 중요한데, 예를 들어 모델을 평가한 결과 6개의 포인트가 인라이어로 분류되었다면, 이는 해당 모델이 주어진 데이터에 대해 상당히 잘 맞는다는 것을 의미한다. 이렇게 계산된 인라이어의 개수는 모델의 품질을 평가하는 점수(score)로 사용되며, RANSAC 알고리즘은 여러 번 반복하여 이 점수를 최대화하는 모델을 찾아내는 과정으로 진행된다. 이 점수 기반 접근 방식은 아웃라이어의 영향을 줄이고, 데이터의 주 패턴을 보다 정확하게 반영하는 모델을 구하는 데 도움이 된다.
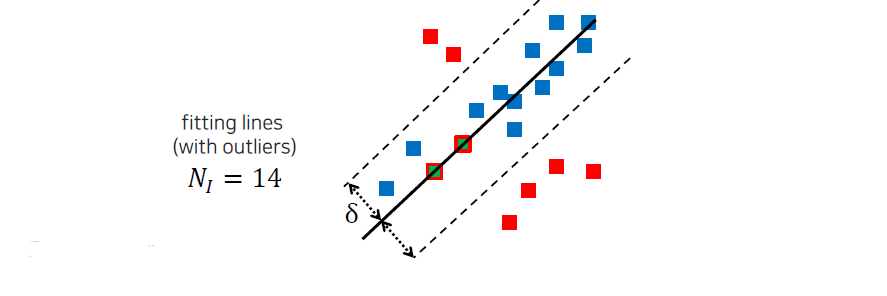
다시 이 과정들을 수행하게 되고, 이때 새롭게 얻은 inlier의 개수가 이전보다 많으면 이를 다시 score로서 사용하게 된다. Inlier가 많다는 것은 현재 model이 더 data에 어울린다는 것을 의미하게 된다. 무작위로 선택된 2개의 point로부터 RANSAC이 시작되기 때문에 어떻게 보면 운이 필요한 algorithm이 된다.
모델이 생성된 후, RANSAC 알고리즘은 주어진 δ(threshold bound)를 기준으로 모델의 품질을 평가한다. 사용자가 설정한 이 δ 값은 모델과 데이터 포인트 간의 허용 가능한 오차 범위를 정의하며, 모델이 얼마나 잘 맞는지를 판단하는 기준이 된다. 데이터 포인트와 모델 간의 거리를 계산하여, 이 거리가 δ 이하인 포인트를 인라이어(inlier)로, δ를 초과하는 포인트를 아웃라이어(outlier)로 분류한다. 이때 인라이어의 개수를 세는 것이 중요하며, 예를 들어 6개의 포인트가 인라이어로 분류되었다면, 이는 해당 모델이 데이터에 대해 적절히 적합하다는 것을 의미한다. 이 인라이어의 개수는 모델의 평가 점수(score)로 활용되며, RANSAC은 여러 번의 반복을 통해 인라이어 수가 최대화되는 모델을 탐색한다. 이러한 점수 기반 접근 방식은 아웃라이어의 영향을 최소화하고 데이터의 주요 패턴을 보다 정확하게 반영하는 모델을 찾는 데 기여한다.
How to choose parameters

RANSAC은 최적의 솔루션을 항상 보장하지 않으며, 이는 알고리즘의 랜덤 특성에 기인한다. RANSAC의 반복 횟수 N을 결정하기 위해서는 먼저 몇 가지 주요 파라미터를 설정해야 한다. 이 중에는 모델을 적합하기 위해 필요한 최소 데이터 포인트 수 s, 아웃라이어 비율 e, 그리고 모델 품질을 평가하기 위한 임계값 δ가 포함된다. 확률 p는 선택한 샘플이 인라이어로 구성될 확률을 나타내며, 이러한 파라미터들은 RANSAC의 반복 횟수 N을 계산하는 데 중요한 역할을 한다. 일반적으로, N은 인라이어가 포함된 모델을 찾기 위해 필요한 반복 횟수로 계산되며, 이때 인라이어의 수가 충분히 많아져야 최적의 모델을 선택할 수 있다. 그러나 이러한 관계는 이론적으로 유도된 것이며, 실제로 이러한 조건들이 항상 만족된다고 보장할 수는 없다. 따라서 RANSAC이 반복적으로 수행되더라도, 최적의 모델이 발견되지 않을 가능성이 존재하므로, 알고리즘 사용 시 주의가 필요하다.
RANSAC step by step

지금까지 line fitting에 대해서 RANSAC을 알아보았는데, 이번에는 homography estimation에서 matching에 outlier가 생겼을 때 어떻게 처리하는지에 대해서 살펴보고자 한다. 먼저 SIFT를 통해서 matching을 찾았다고 해보자.
이제 RANSAC을 활용하여 호모그래피 추정(homography estimation)에서 아웃라이어를 처리하는 방법을 살펴보자. 예를 들어, 이미지 A와 이미지 B가 있을 때, SIFT(Scale-Invariant Feature Transform)를 사용하여 두 이미지 간의 특징점을 추출하고 매칭을 찾았다고 가정하자. 이 과정에서 다수의 매칭 포인트가 생성되지만, 다양한 요인으로 인해 일부 매칭은 아웃라이어가 될 수 있다. 예를 들어, 이미지 A의 특정 특징점이 이미지 B의 유사한 위치에 잘못 매칭되었거나, 장면의 변화로 인해 다른 객체가 포함되었을 수 있다. 이럴 때, RANSAC 알고리즘을 적용하여 랜덤하게 선택된 매칭 포인트들로부터 호모그래피 모델을 계산하고, δ라는 임계값을 기준으로 인라이어와 아웃라이어를 구분한다. 이렇게 함으로써, 실제로 올바른 매칭을 기반으로 한 호모그래피 변환을 추정할 수 있으며, 아웃라이어의 영향을 최소화하여 더욱 정확한 결과를 도출할 수 있다.

그러면 위와 같이 outlier로부터 만들어진 correspondence와 inlier로부터 만들어진 correspondence들이 함께 존재할 것이다.
위의 상황에서 아웃라이어와 인라이어로부터 만들어진 매칭이 함께 존재하게 된다. 예를 들어, 이미지 A에서의 특징점 P1이 이미지 B의 잘못된 위치 Q1과 매칭되었다면, 이는 아웃라이어에 해당한다. 반면, 이미지 A의 특징점 P2가 이미지 B의 올바른 위치 Q2와 매칭되었다면, 이는 인라이어로 간주된다. 이러한 매칭이 혼재된 상태에서 RANSAC을 통해 아웃라이어를 제거하는 과정이 필요하다. RANSAC 알고리즘은 반복적으로 랜덤하게 선택된 인라이어 매칭 포인트들로 호모그래피 모델을 계산하고, 그 모델을 기반으로 δ 임계값을 사용하여 인라이어와 아웃라이어를 구분한다. 이 과정에서 유효한 매칭은 인라이어로 분류되어 최종 모델의 품질을 향상시키고, 아웃라이어는 제거되어 전체 매칭의 정확성을 높이는 데 기여한다. 최종적으로, 남은 인라이어들로부터 더욱 신뢰할 수 있는 호모그래피 추정 결과를 얻을 수 있다.
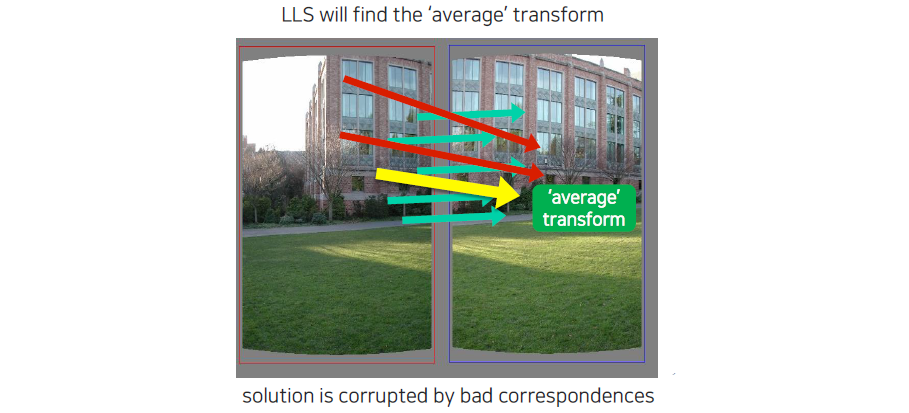
처음에는 linear least square를 사용해서 average transform을 찾아야 한다. Outlier로 인해서 아래로 화살표가 가는 것을 볼 수 있다. 이는 outlier의 영향이 더 크다고 판단할 수 있는 것이다.
처음에는 선형 최소 제곱법(linear least squares)을 사용하여 평균 변환(average transform)을 찾게 된다. 이때 데이터 포인트들이 평균으로부터 어떻게 분포하는지를 평가하게 되며, 아웃라이어의 존재는 결과에 큰 영향을 미칠 수 있다. 예를 들어, 아웃라이어가 포함된 데이터 세트에서 선형 모델을 적합시키면, 아웃라이어가 실제 데이터보다 훨씬 멀리 위치할 수 있어 모델의 기울기나 절편이 왜곡되어 평균 변환을 아래로 밀어내는 결과를 초래할 수 있다. 이는 아웃라이어의 영향력이 더 크다는 것을 나타내며, 따라서 이로 인해 구해진 평균 변환이 실제 데이터의 패턴을 잘 반영하지 못하게 되는 상황이 발생한다. 이러한 문제를 해결하기 위해 RANSAC과 같은 알고리즘을 사용하여 아웃라이어를 제거하고, 보다 신뢰할 수 있는 변환을 찾는 과정이 필요하다.
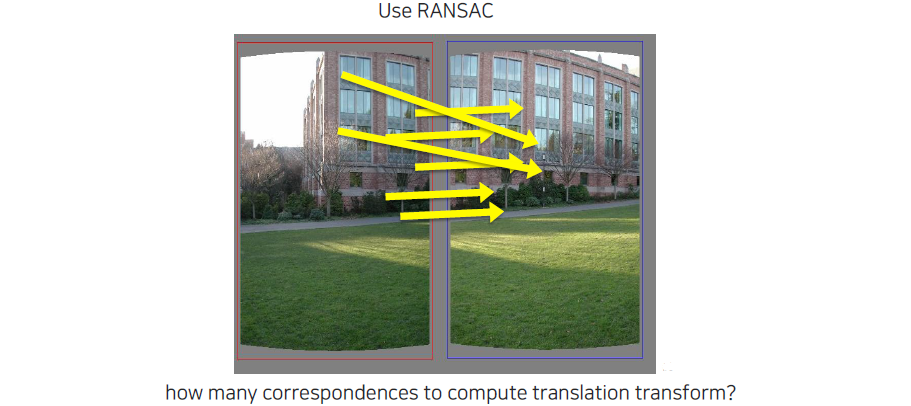
우리는 translation을 구하기 때문에 하나의 correspondence만 있어도 motion vector를 구할 수 있다. 그래서 RANSAC model을 sampling할 때 필요한 correspondence sample 개수는 하나이다. 우리는 무작위로 하나의 pair씩만 sampling하면 된다.
우리가 구하고자 하는 변환이 단순히 평행 이동(translation)이라면, 단일 correspondence(매칭 쌍)만으로도 motion vector를 구할 수 있다. 이 경우, RANSAC 모델을 샘플링할 때 필요한 correspondence sample 개수는 하나로 충분하다. 즉, RANSAC은 무작위로 하나의 매칭 포인트 쌍을 선택하여 이들로부터 변환 벡터를 계산할 수 있다. 이 과정은 매우 효율적이며, 각 반복에서 하나의 매칭 쌍만을 사용하여 모델을 생성하므로, 아웃라이어가 포함된 데이터 세트에서도 모델을 신속하게 업데이트하고 평가할 수 있는 장점이 있다. 이렇게 얻어진 motion vector는 반복적인 샘플링을 통해 인라이어의 수를 늘리고, 최종적으로 가장 많은 인라이어를 가진 변환을 찾는 데 기여하게 된다.
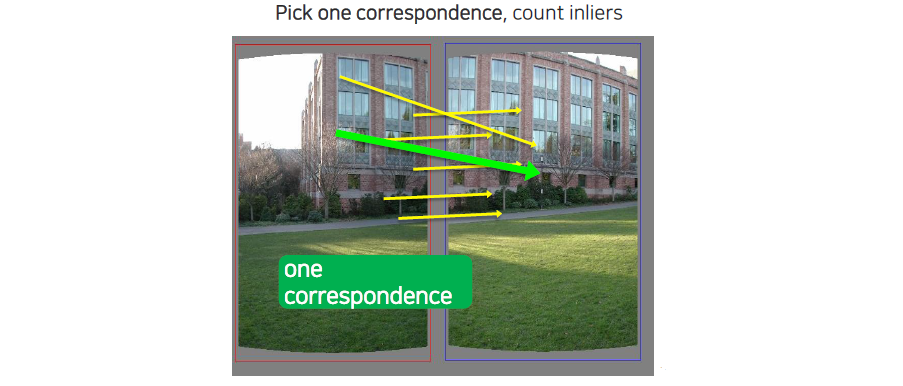
하나를 sampling하게 되면 correspondence가 나오게 되고 이에 따른 inlier를 셀 수가 있다.
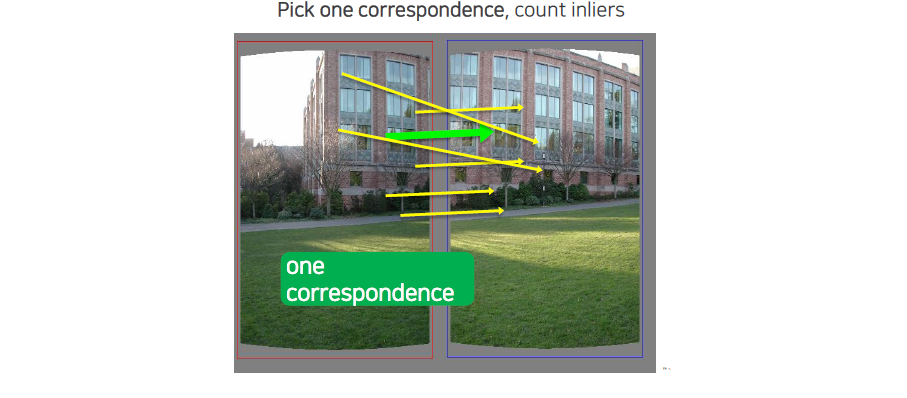
우리가 어느 것을 선택하는지에 따라서 inlier의 개수가 달라지게 된다.
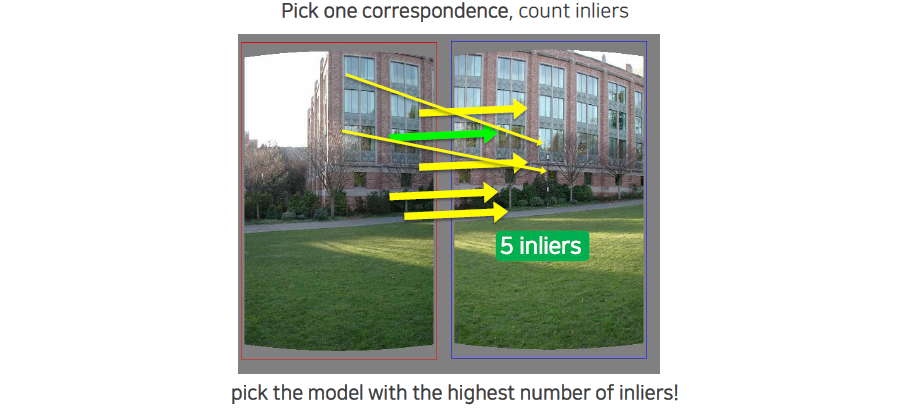
우리는 sampling을 할 때마다 inlier의 개수를 세서 가장 많은 inlier가 생기는 것을 최종적으로 선택하게 될 것이다. 선택되 model에 의해서 outlier들을 제외시킬 수가 있고, 이로 인하여 robust한 parameter estimation이 가능해지게 된다.
Estimating homography using RANSAC

호모그래피를 구하는 과정에서 RANSAC은 다음과 같은 순서로 진행된다. 먼저, 4개의 포인트 correspondence를 무작위로 선택한다. 호모그래피 행렬 H를 계산하기 위해서는 자유도(degrees of freedom, DoF)가 8이므로, 4개의 포인트 correspondence가 필요하다. 이후 선택된 포인트 쌍을 기반으로 DLT(Direct Linear Transform)를 통해 호모그래피 H를 계산한다. 그 다음에는 계산된 H를 사용하여 각 포인트 P를 변환하여 새로운 점 P′를 얻는다. 이렇게 변환된 점 P′와 원래 매칭된 점 P′ 간의 거리를 계산하고, 이 거리가 미리 설정한 임계값(threshold)보다 작으면 해당 포인트를 인라이어로 간주한다. 예를 들어, 변환된 포인트 P′와 매칭된 포인트 P′ 사이의 거리가 2픽셀 이하라면 이 포인트는 인라이어로 분류된다. 이 과정을 통해 인라이어의 개수를 세고, 반복적으로 진행하면서 가장 많은 인라이어를 가지는 호모그래피 H를 선택한다. 마지막으로, 이렇게 선택된 인라이어들을 사용하여 다시 DLT를 통해 H를 보정하여 최종적으로 더 정확한 호모그래피를 얻는다. 이 방법은 아웃라이어의 영향을 최소화하고, 실제 데이터에 더 잘 맞는 모델을 추정하는 데 효과적이다.
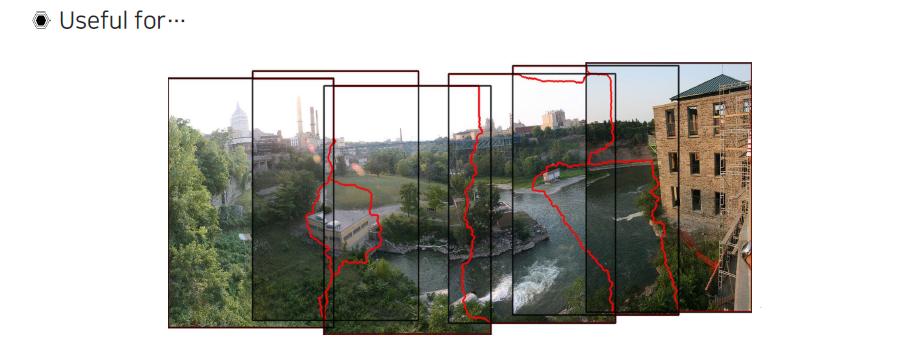
이러한 RANSAC은 panorama estimation이나 3D reconstruction에서 굉장히 중요한 algorithm이고 여러 parameter estimation에서 많이 사용되는 방법 중 하나이다. 이는 굉장히 실용적이고 속도도 빠른편에 해당한다.
The image correspondence pipeline
Image의 대응점을 찾는 pipeline을 보면 중요한 point를 찾는 feature point detection 후에 이를 잘 설명하는 feature point description이 존재해야 하고, descriptor끼리 유사도를 비교해서 만든 matching으로부터 존재하는 outlier들을 filtering하는 RANSAC algorithm까지 필요하다. 이러한 과정을 통해서 panorama estimation이나 3D reconstruction 등 다양한 것을 할 수 있게 된다.
Hough Transform (허프 변환)
허프 변환(Hough Transform)은 이미지에서 직선, 원 등 특정 기하학적 패턴을 감지하는 데 사용되는 기법으로 노이즈나 부분적 왜곡에 강하다. 직선을 검출할 때 허프 변환은 이미지 공간에서 각 에지 픽셀의 위치를 이용해 허프 공간이라는 새로운 파라미터 공간으로 변환하여 직선을 (ρ,θ) 형태로 표현한다. 여기서 ρ는 이미지 원점에서 직선까지의 수직 거리이며, θ는 원점에서 직선까지의 수직선과 직선이 이루는 각도를 의미한다. 에지 픽셀 하나하나가 다양한 각도의 직선 위에 있을 수 있기 때문에 각 에지 픽셀에 대해 가능한 모든 (ρ,θ) 값을 계산하고, 이 값을 허프 공간에서 해당하는 위치에 투표하는 방식으로 진행된다. 여러 에지 픽셀의 투표가 동일한 (ρ,θ)에 집중되면, 이는 이미지 내에 강한 직선이 존재함을 나타내는 것으로 해석된다. 이렇게 허프 변환은 이미지의 각 픽셀이 기여하는 파라미터 공간의 축적된 정보를 바탕으로 직선 패턴을 감지하고, 에지들이 일관되게 특정 (ρ,θ)에 투표할 때 이를 직선으로 추출해 이미지 속 기하학적 형태를 효과적으로 식별할 수 있도록 돕는 것이다.
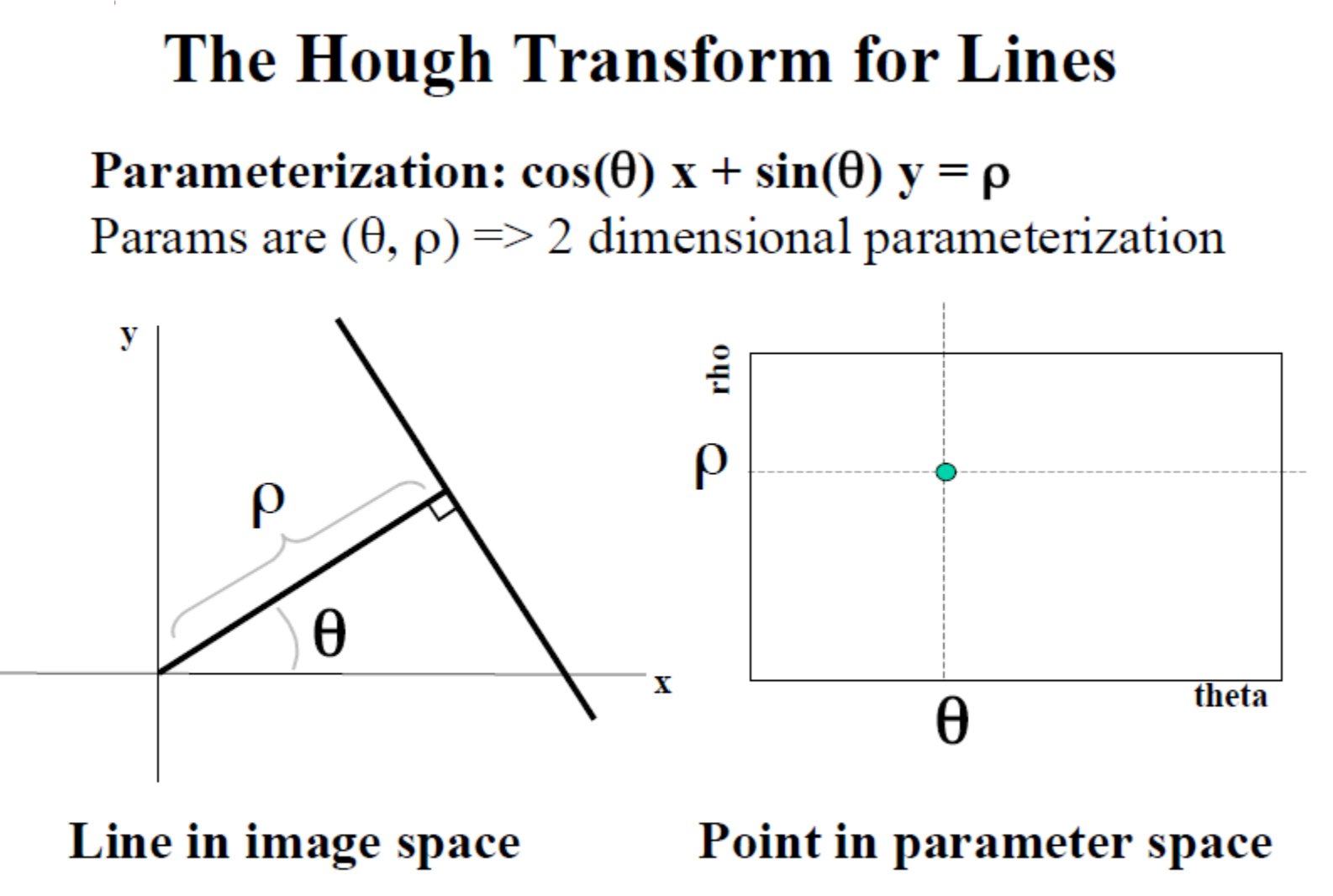
직선은 일반적으로 y=mx+c 형태의 일차 방정식으로 표현되지만 이 방식은 수직선의 경우 기울기(m)가 무한대가 되어 표현이 어려운 한계가 있다. 허프 변환은 이러한 한계를 극복하기 위해 직선을 극좌표계의 형태로 표현하여 모든 직선을 파라미터로 다룰 수 있도록 한다. 극좌표계에서는 직선을 ρ와 θ로 표현하는데, 여기서 ρ는 이미지 원점에서 직선까지의 최소 수직 거리이고, θ는 이 수직선과 직선 사이의 각도를 의미한다. 이러한 표현 방식에서 직선은 ρ = xcos(θ) + ysin(θ)로 나타나며 이미지 내의 각 에지 픽셀이 가질 수 있는 모든 직선에 대한 ρ와 θ 값을 계산하여 허프 공간에서의 위치에 투표하는 방식으로 직선을 찾는다. 이로 인해 수직선이나 기울기가 큰 직선들도 모두 일관된 방식으로 허프 공간에서 표현될 수 있어, 허프 변환은 다양한 형태의 직선 검출에 유연하게 적용될 수 있는 것이다.

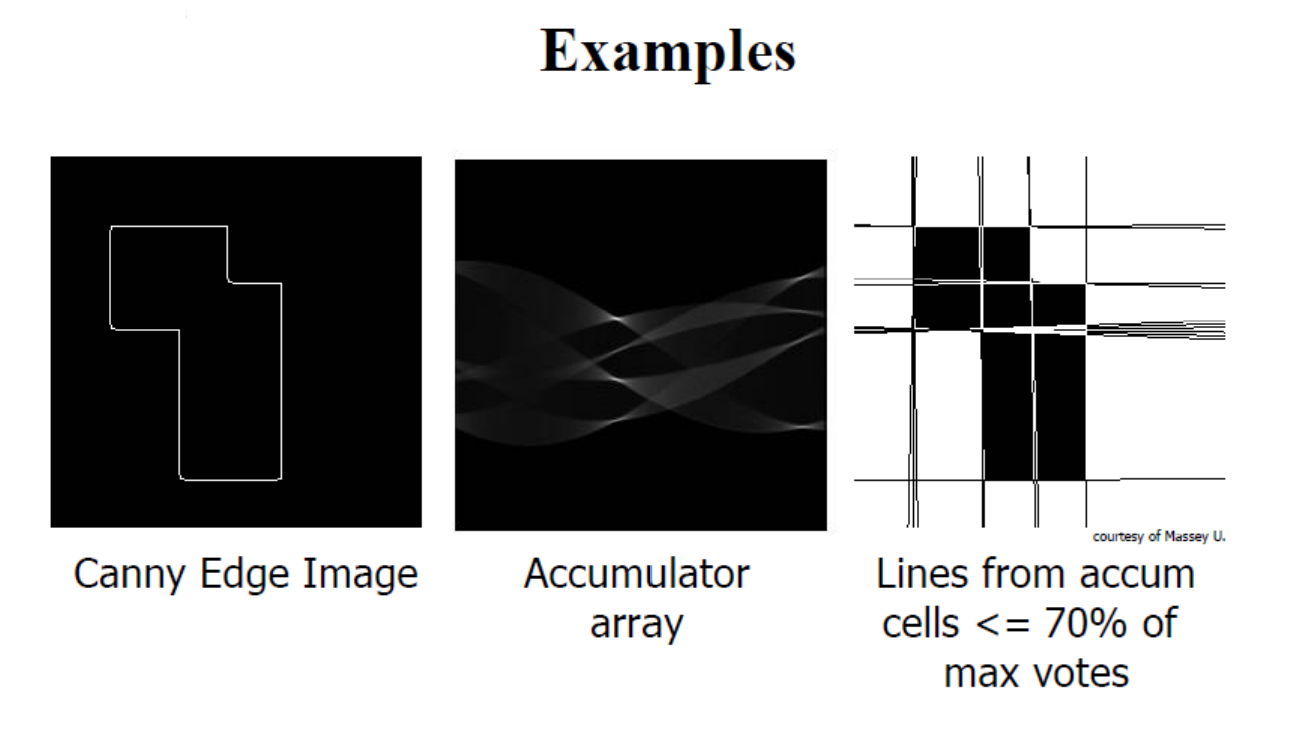
허프 변환에서는 직선을 ρ와 θ라는 두 매개변수로 표현하여 허프 공간(Hough space)이라는 2D 배열에 저장된다. 이 배열에서 행(row)은 ρ 값을, 열(column)은 θ 값을 나타내며, 배열의 크기는 원하는 각도와 거리의 정확도에 따라 결정된다. 일반적으로 θ 값은 0°에서 180°까지 1° 간격으로 나뉘어 180개의 열을 갖게 된다. 예를 들어 N×N 픽셀 이미지에 대해 허프 변환을 적용하려면, 먼저 Canny Edge 검출 같은 알고리즘을 사용하여 이미지의 에지 픽셀을 구한다. ρ 값의 최대 범위는 이미지 대각선 길이(√(N² + N²))가 되며, θ는 0°에서 180° 범위로 설정된다. 각 에지 픽셀에 대해 가능한 모든 θ 값에 대해 ρ = xcos(θ) + ysin(θ) 식으로 ρ 값을 계산하고, 계산된 (ρ,θ) 좌표의 허프 공간 위치에 투표를 진행한다. 모든 에지 픽셀의 투표가 끝난 후, 허프 공간에서 가장 높은 투표수를 가진 셀들이 강한 직선을 나타내며, 해당 (ρ,θ) 값은 이미지 내 직선의 매개변수로 해석된다.
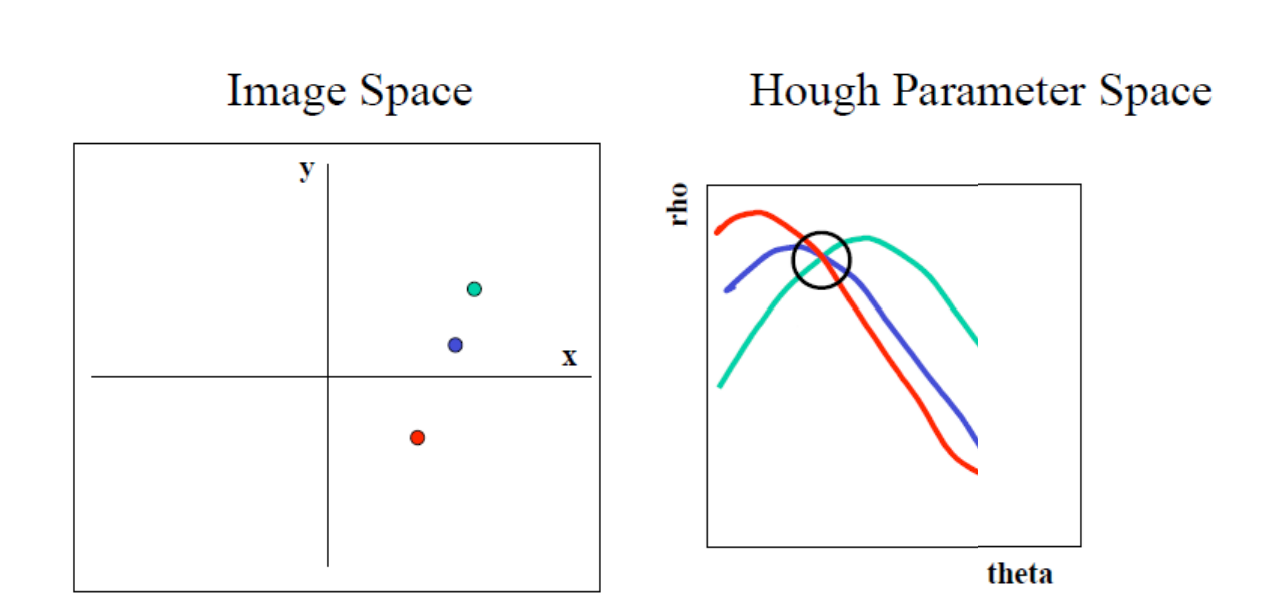
그러나 허프 공간에 여러 노이즈 점이 있다면, 특정 직선의 검출이 어려워진다. 이때 노이즈와 겹치는 상황을 줄이려면 허프 공간에서 특정 (ρ, θ) 값에 대한 누적값(voting)들이 높은 곳을 찾아야 한다. 노이즈가 많으면 누적값이 분산되므로, 고정된 임계값 설정이 어렵다. 노이즈를 줄이기 위해 가우시안 필터 등을 허프 공간에 적용하거나, 허프 공간 누적값을 기반으로 지역 최대값을 찾는 비최대 억제(non-maximum suppression) 기법을 쓸 수 있다. 현실적으로 이미지의 특성과 노이즈를 고려해 적절한 필터링과 임계값을 조절하고, 노이즈 점의 비율을 줄여야 정확한 직선을 감지할 수 있다.
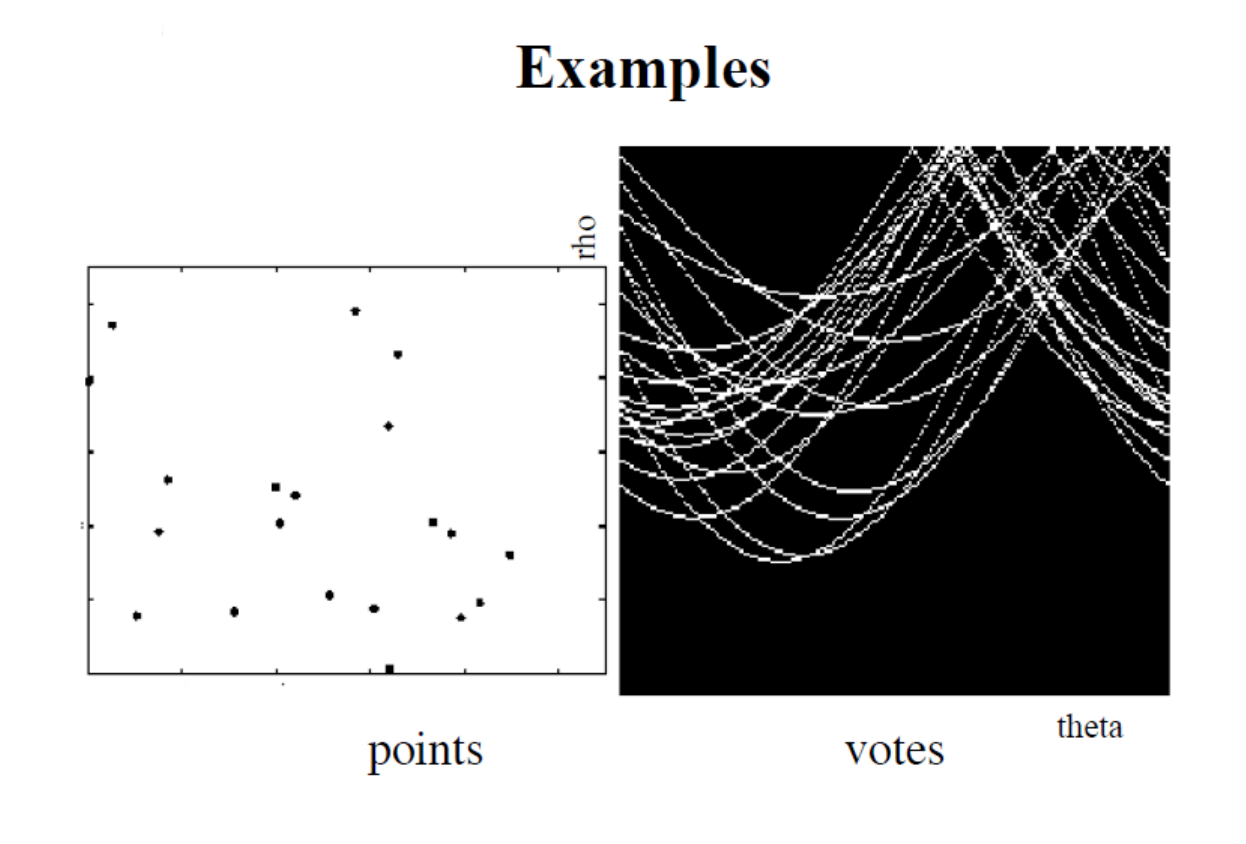
블러링과 스무딩은 영상 처리나 데이터 분석에서 노이즈를 줄이고 주요 흐름을 파악하는 데 유용한 기술이다. 예를 들어, 블러링은 이미지에서 세부 사항을 희미하게 하여 전체적인 형태나 패턴을 강조하는 데 쓰인다. 이 과정에서 값의 변화를 약간만 표시하면서, 큰 트렌드나 전반적인 흐름을 포착할 수 있다. 다만, 과도한 블러링은 원본 데이터의 세부 정보를 잃게 할 위험이 있다. 스무딩도 유사하게 적용되며, 스무딩 필터는 노이즈를 줄이는 동시에 큰 범위에서의 형태 인식은 높인다. 하지만 디테일이 줄어들고 특정 중요한 정보가 사라질 수 있는 단점이 존재한다. 이를 해결하기 위해, 분석 윈도우 크기를 조정하거나 디테일과 전체 흐름 간의 균형을 맞추는 것이 중요하다.
Hough 변환은 이미지에서 선이나 곡선 등 특정 패턴을 찾는 방법으로, 특히 X-Y 좌표 평면에서 특정 모양(예: 선)을 식별하는 데 유용하다. Hough 변환을 LCF(로컬 컨셉 프레임)와 연결하면, 디지털 이미지에서 실제 물체의 형상을 정확히 표현하려 할 때 유용하다. LCF는 X와 Y 값을 조정하여 물체의 시각적 표현을 최적화하고자 하는 반면, Hough 변환은 이미지 내에서 해당 물체의 가장자리를 식별하고, 특정 패턴(예: 직선)의 위치를 정확히 추출할 수 있도록 돕는다. Hough 변환을 통해 잡은 패턴을 기반으로 LCF는 디스플레이의 각 픽셀 위치에 대한 정확한 좌표를 계산하고, 디지털 노이즈로 인한 왜곡이나 해상도 저하 등의 문제를 보완하여 더욱 직관적이고 사실적인 표현을 가능하게 한다.
Hough Transform for Circles
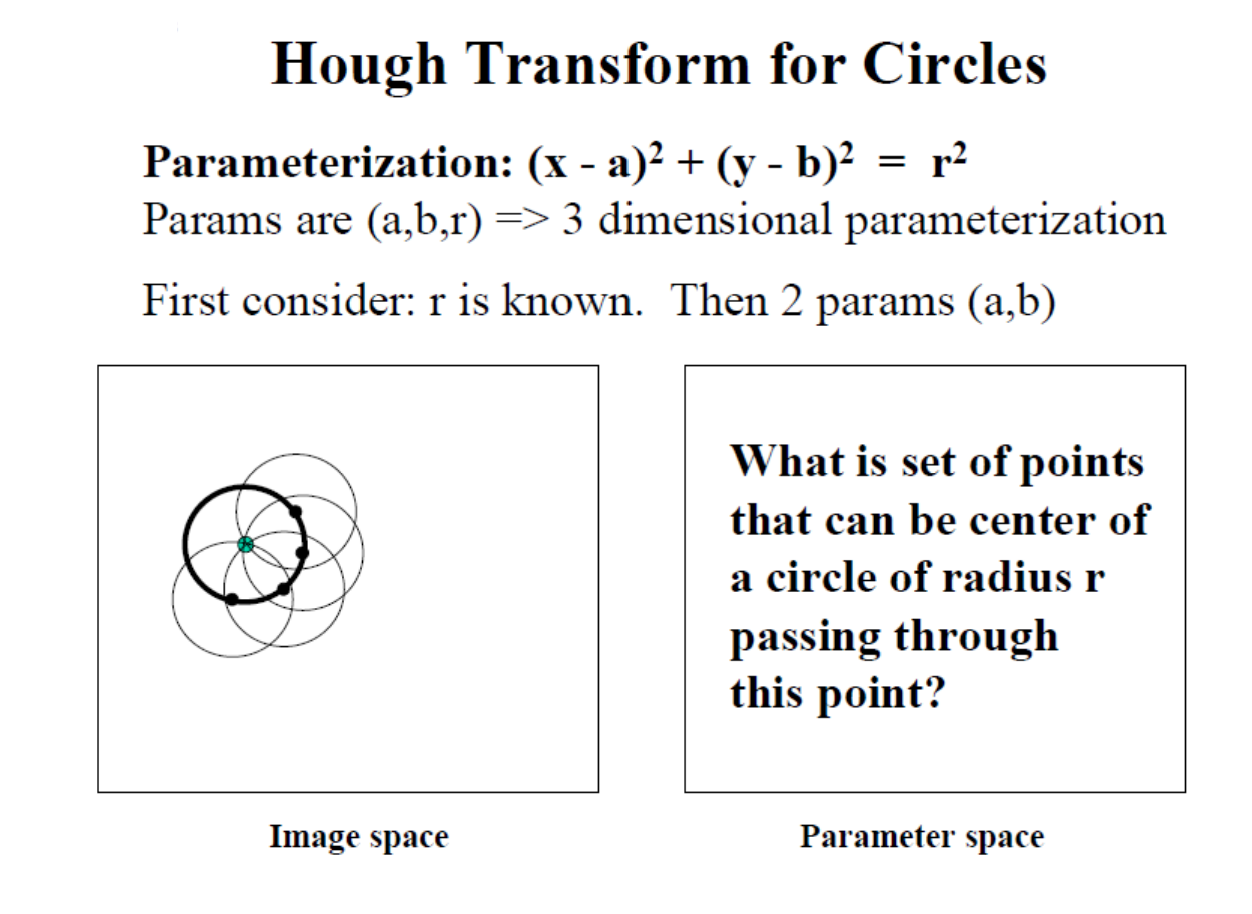
원을 탐지할 때는 중심 좌표(X, Y)와 반지름 R이라는 세 가지 변수가 필요한데, 이 변수 조합을 통해 여러 원 후보를 평가할 수 있다. 각 원의 중심을 추정하기 위해, 중심 후보들을 누적해 가장 많은 점을 포함하는 원을 찾는 방식으로 Hough 변환이 작동한다. 이때 반지름 R이 정해져 있다면 파라미터 공간은 2차원이지만, 반지름이 자유 변수일 경우에는 3차원 파라미터 공간을 필요로 한다. 이는 다양한 반지름에 대해 같은 중심을 갖는 여러 원을 분석하여 최적의 반지름을 찾을 수 있게 한다. 이와 같이 모든 가능한 파라미터 조합을 전수 조사하는 '풀 서치' 방식은 계산 비용이 크지만, Hough 변환은 해당 공간을 효율적으로 탐색하여 특정 패턴을 추출하는 데 유리하다. 따라서, 이 변환을 활용하여 점들이 특정 형상을 이루는지를 파악하고, 원의 중심 좌표와 반지름 등 각 파라미터를 최적화할 수 있는 것이다.
Hough Transform의 구현 (직선 검출하기)
Hough Transform을 이용해서 이미지 내 직선을 검출하여 보자. (python, opencv 구현 코딩)
Hough Transform (Standard)
# 표준 허프 변환
lines_standard = cv2.HoughLines(edges, 1, np.pi/180, 132)
"""
cv2.HoughLines() parameters
1. edges -> edge pixel image (input image name)
2. 1 -> 거리 해상도(rho, generally use 1 pixel)
3. np.pi/180 -> 각도 해상도. 위에서 설명한
정확도에 따른 배열 크기 값(theta, generally use 1°)
4. 132 -> threshold value (직선 결정을 위한 최소 투표 수)
"""
# 표준 허프 변환으로 찾은 직선 그리기
if lines_standard is not None:
for line in lines_standard:
rho, theta = line[0]
a = np.cos(theta) # θ에서의 cosine 값
b = np.sin(theta) # θ에서의 sin 값
x0 = a * rho # 직선과 x축이 만나는 점의 x 좌표
y0 = b * rho # 직선과 y축이 만나는 점의 y 좌표
x1 = int(x0 + 1000 * (-b))
# x1 : 직선 위의 한 점으로부터 직선을 따라 왼쪽으로 1000 픽셀 떨어진 점의 x 좌표
y1 = int(y0 + 1000 * (a))
# y1 : 동일한 점으로부터 위쪽으로 1000 픽셀 떨어진 점의 y 좌표
x2 = int(x0 - 1000 * (-b))
# x2 : 직선 위의 한 점으로부터 직선을 따라 오른쪽으로 1000 픽셀 떨어진 점의 x 좌표
y2 = int(y0 - 1000 * (a))
# y2 : 동일한 점으로부터 아래쪽으로 1000 픽셀 떨어진 점의 y 좌표
cv2.line(image, (x1, y1), (x2, y2), (0, 0, 255), 2)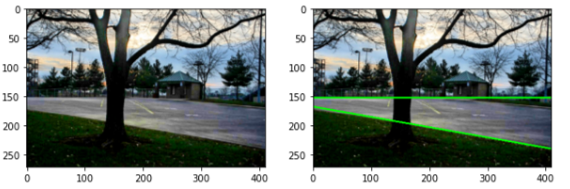
Probabilistic Hough Transform
확률적 허프 변환은 표준 허프 변환의 변형으로, 모든 픽셀을 사용하는 것이 아닌, 임의의 픽셀의 부분 집합만을 사용하여 계산 효율성을 개선하였다.
# 확률적 허프 변환
lines_probabilistic = cv2.HoughLinesP(edges, 1, np.pi/180, 132,
minLineLength=100, maxLineGap=10)
"""
cv2.HoughLinesP() parameters
1. edges -> edge pixel image (input image name)
2. 1 -> 거리 해상도(rho, generally use 1 pixel)
3. np.pi/180 -> 각도 해상도. 위에서 설명한
정확도에 따른 배열 크기 값(theta, generally use 1°)
4. 132 -> threshold value (직선 결정을 위한 최소 투표 수)
5. 100 -> minLineLength (직선으로 감지되는 최소 길이, 이보다 짧으면 무시)
6. 10 -> minLineGap (직선으로 감지되기 위하여 선분 사이 허용되는 최소 간격)
(이 값이 크면 끊어진 선분을 하나로 잇는 데 용이하나, 너무 크면 관련없는 선분이
연결될 수 있으므로 주의)
"""
# 확률적 허프 변환으로 찾은 직선 그리기
if lines_probabilistic is not None:
for line in lines_probabilistic:
x1, y1, x2, y2 = line[0]
cv2.line(image, (x1, y1), (x2, y2), (0, 255, 0), 2)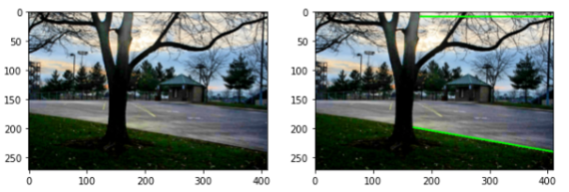
여기서 설정된 임계값은, 테스트 이미지에 맞게 적당히 올리고 내려가면서 수동으로 맞춰 주었다.
- 결과 비교

'Camera & Vision > Computer Vision' 카테고리의 다른 글
| Vision Theory [5] : 영상 분할 (0) | 2024.11.07 |
|---|---|
| Vision Theory[3] : 카메라 모델과 스테레오 비젼 (1) | 2024.10.13 |
| Vision Theory [2] : 에지 & 코너 검출 및 포인트 매칭 (2) | 2024.09.28 |
| Vision Theory [1] : 이미지의 정보와 처리 (3) | 2024.09.19 |






