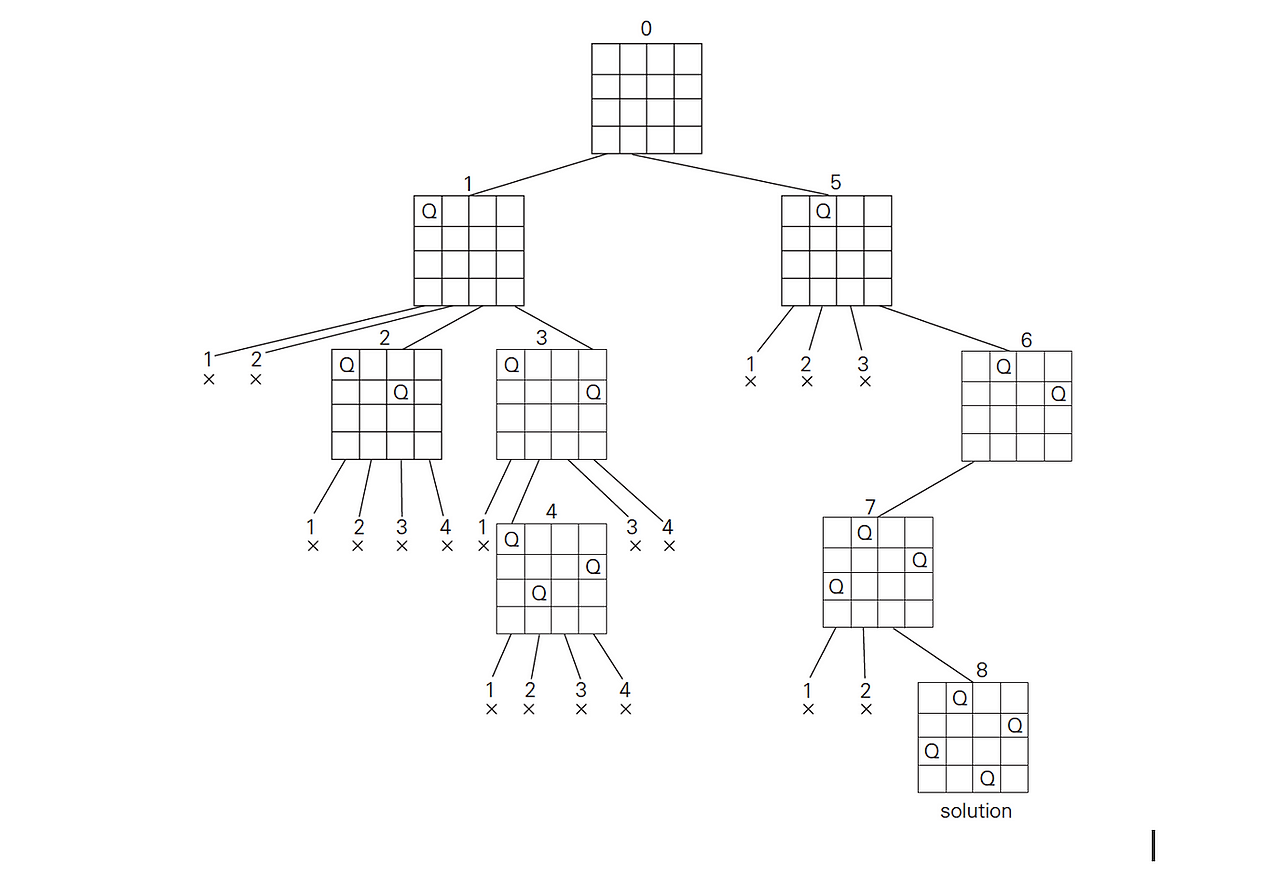
1. 백트레킹 (Back Tracking)

백트래킹(backtracking) 알고리즘은 탐색 문제를 해결하는 기법으로, 상태공간트리를 깊이우선탐색(DFS) 방식으로 탐색하면서 유망하지 않은 노드(non-promising node)를 가지치기(pruning) 하여 탐색 범위를 줄인다. 이 알고리즘은 탐색 중간에 해답이 나올 가능성이 없는 경로를 제거해 효율성을 극대화한다.
깊이 우선 탐색 (Depth-First Search, DFS)
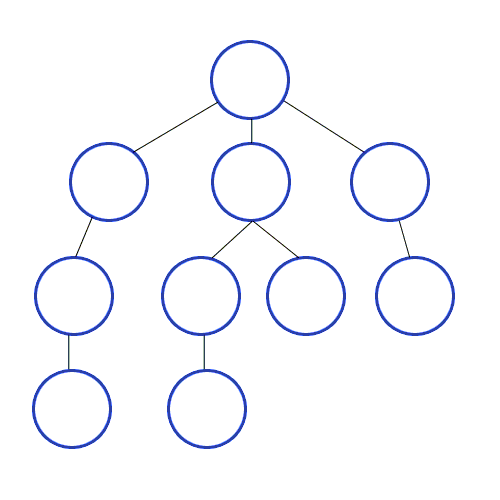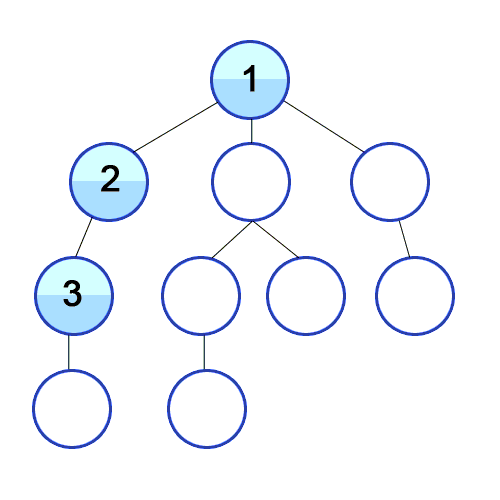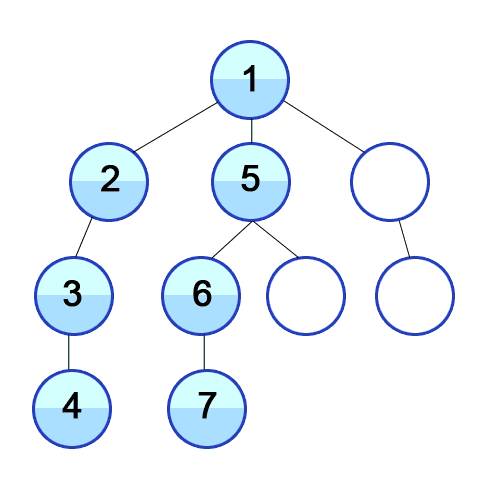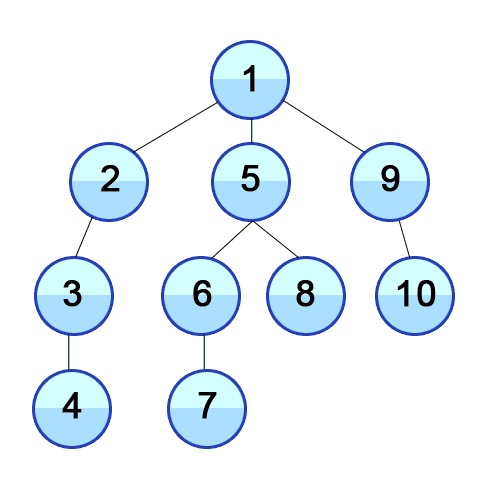
깊이우선탐색(Depth-First Search; DFS)은 트리나 그래프 구조에서 루트 노드(또는 시작 노드)부터 시작하여, 자식 노드를 깊게 탐색한 후 더 이상 자식 노드가 없을 때 부모 노드로 되돌아오는 방식으로 진행하는 탐색 알고리즘이다. 이는 주로 재귀적으로 구현되며, 특정 노드를 방문한 뒤 그 노드의 모든 후손 노드(보통 왼쪽에서 오른쪽 순서로)를 차례로 탐색하는 과정을 반복한다. DFS는 트리 구조에서 선순위(preorder) 순회와 유사하며, 상태공간트리의 탐색이나 경로 찾기 문제 등 다양한 알고리즘에서 기본으로 사용된다.
void depth_first_tree_search(node v) {
node u;
visit v; // 뿌리 노드 방문
for (each child u of v)
depth_first_tree_search(u); // 자식 노드 탐색
}상태공간트리(state space tree)
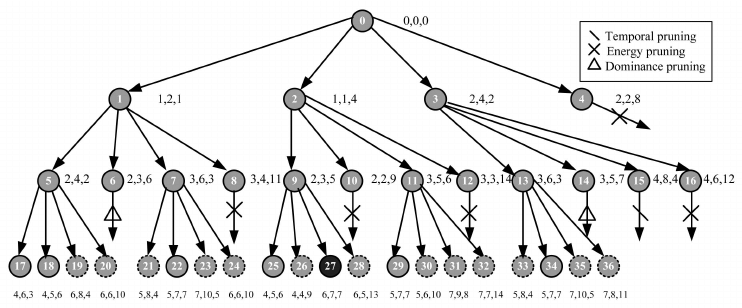
상태 공간 트리는 문제 해결을 위한 탐색 과정을 구조화하여 표현하는 계층적 트리 구조다. 이 트리는 탐색 문제에서 가능한 모든 상태를 노드로 나타내며, 뿌리 노드 (root node)부터 잎 노드 (leaf node)까지의 경로는 해답 후보(candidate solution)를 의미한다. 상태공간트리는 백트래킹이나 깊이우선탐색(DFS)과 같은 알고리즘에서 활용되며, 탐색 공간을 효율적으로 다루기 위해 사용된다.
뿌리 노드는 초기 상태를 나타내며, 탐색의 출발점이 된다. 각 내부 노드(inner node)는 탐색 과정 중 중간 상태를 나타내고, 그 자식 노드는 다음 단계에서 탐색 가능한 상태를 나타낸다. 잎 노드는 탐색이 종료된 상태로, 해답인지 아닌지에 따라 선택된다. 하지만 이 트리는 일반적으로 암묵적(implicit)으로 표현되며, 실제로 트리를 생성하지 않고 탐색 과정에서 필요한 부분만 계산하여 메모리 사용을 절약한다.
상태공간트리는 특정 문제를 해결하기 위해 유망(promising)한 상태와 그렇지 않은 상태를 구분한다. 예를 들어, n-Queens 문제에서는 체스판에서 퀸이 서로 위협하지 않도록 배치해야 한다. 이 문제에서 상태공간트리의 각 노드는 특정 행에 퀸을 배치한 상태를 나타내며, 유망하지 않은 노드는 같은 열이나 대각선에 다른 퀸이 존재하는 상태로 판단해 가지치기(pruning)하여 탐색을 중단한다. 마찬가지로, 부분집합 합 문제에서는 현재까지 선택된 아이템의 합과 남은 아이템의 총합으로 목표 합을 만들 수 없는 경우를 비유망(non-promising) 상태로 판단하여 탐색 범위를 줄인다.
백트래킹의 핵심은 유망성(promising)을 판별하는 것이다. 탐색 중 현재 노드가 유망하다면(즉, 해답이 될 가능성이 있다면) 그 자식 노드를 계속 탐색한다. 반대로 유망하지 않다고 판단되면 해당 노드와 그 하위 노드를 탐색하지 않고 바로 부모 노드로 되돌아간다. 이 과정에서 불필요한 탐색을 피하게 되며, 탐색해야 할 상태공간의 크기를 크게 줄일 수 있다.
백트래킹 알고리즘의 일반적인 절차는 다음과 같다.
- 상태공간트리를 깊이우선탐색(DFS)으로 순회한다.
- 각 노드에 대해 유망성을 검사한다.
- 유망하지 않은 노드는 탐색을 중단하고 부모 노드로 되돌아간다.
- 유망한 노드는 자식 노드를 계속 탐색하며, 해답에 도달하면 이를 기록하거나 출력한다.
백트래킹 알고리즘은 탐색 문제에서 해답 후보를 효과적으로 좁히고, 불필요한 계산을 줄여 문제 해결의 효율성을 높이는 강력한 기법이다. N-Queens 문제와 부분집합의 합 문제는 이러한 백트래킹의 원리를 잘 설명해주는 대표적인 사례다.
void checknode(node v) {
node u;
if (promising(v)) {
if (there is a solution at v) {
write the solution; // 해답 출력
} else {
for (each child u of v) {
checknode(u); // 자식 노드 탐색
}
}
}
}N - Queens

N-Queens 문제는 체스판 위에 N개의 퀸을 배치하되, 각 퀸이 서로 위협하지 않도록 배치하는 문제다. 퀸은 체스의 말 중 하나로, 같은 행, 열, 또는 대각선에 있는 다른 말을 공격할 수 있다. 따라서 N-Queens 문제의 해답은 N x N 체스판에서 N개의 퀸이 서로 공격하지 않도록 배치한 모든 가능한 경우를 찾는 것이다.
이 문제는 상태공간트리를 활용하여 탐색할 수 있다. 상태공간트리의 각 노드는 특정 행에 퀸이 배치된 상태를 나타내며, 트리의 깊이는 배치된 퀸의 개수를 의미한다. 탐색은 깊이우선탐색(DFS) 방식으로 진행되며, 백트래킹을 통해 유망하지 않은 상태를 가지치기(pruning)하여 탐색 범위를 줄인다. 가지치기를 위한 유망성(promising)의 조건은 현재 퀸이 배치된 상태에서 다른 퀸과 같은 행, 열, 또는 대각선에 위치하지 않는지 검사하는 것이다.
예를 들어, 4-Queens 문제를 생각해보자. 이 문제에서는 4 x 4 체스판에 4개의 퀸을 배치해야 하며, 가능한 배치 조합은 상태공간트리를 통해 탐색한다. 단순한 깊이우선탐색을 사용하면 4^4 = 256가지의 경우를 모두 검사해야 하지만, 백트래킹을 통해 불가능한 경로를 제거하면 탐색해야 할 노드의 개수를 대폭 줄일 수 있다. 실제로, 백트래킹을 활용하면 탐색해야 할 노드의 수는 27개로 줄어든다.
- 기본 탐색:
- 첫 번째 행부터 시작해, 각 행에 하나씩 퀸을 배치한다.
- 열(column)과 대각선(diagonal)의 제약 조건을 만족하는 경우에만 다음 행으로 진행한다.
- 모든 퀸을 배치하면 해답(solution)으로 기록한다.
- 유망성 판단(promising):
- 현재 배치가 유망하지 않으면 탐색을 중단하고, 이전 단계로 돌아간다.
- 유망성은 두 퀸이 같은 열이나 대각선에 위치하지 않음을 확인함으로써 판단한다.
- 재귀적 호출:
- 각 행에 대해 가능한 열을 탐색하면서 유망성을 만족하면 재귀적으로 다음 행으로 탐색을 이어간다.
- 상태공간트리와 가지치기 (pruning)
- 상태공간트리의 각 노드는 현재까지 배치된 퀸의 상태를 나타낸다.
- 백트래킹을 통해 유망하지 않은 노드를 가지치기하여 탐색하지 않는다. 예를 들어, 4-Queens 문제에서는 단순 DFS로 85개의 노드를 탐색해야 하지만, 백트래킹을 사용하면 탐색해야 할 노드의 수가 27개로 줄어든다
복잡도 분석
N-Queens 문제의 백트래킹 알고리즘의 시간 복잡도는 상태공간트리에서 탐색해야 하는 노드의 수에 의해 결정된다. 이를 분석하기 위해 상태공간트리의 구조와 백트래킹이 가지치기를 통해 탐색 범위를 얼마나 줄이는지를 고려해야 한다.
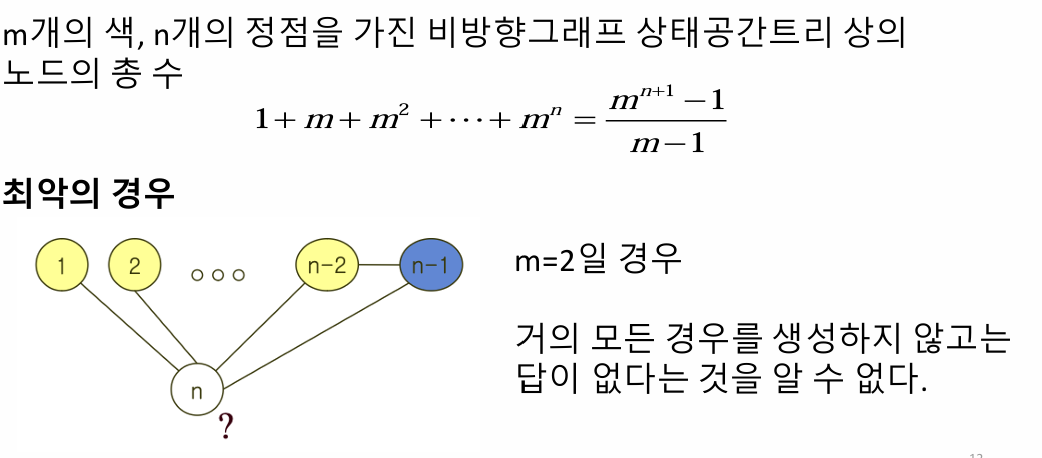
1. 상태공간트리의 전체 노드 수 기반 분석
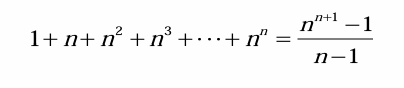
첫 번째 분석 방식은 상태공간트리에 존재하는 모든 노드의 개수를 계산하여 시간복잡도를 평가하는 것이다. 예를 들어, n-Queens 문제에서 상태공간트리의 깊이는 n이고, 깊이가 i인 노드의 개수는 ni로 나타난다. 전체 상태공간트리의 노드 개수는 1+n+n2+⋯+nn으로 계산되며, 이는 대략적으로 O(n^n)의 시간복잡도를 갖는다. 이 방식은 트리의 모든 노드를 탐색한다고 가정하므로, 실제 백트래킹에서 가지치기가 발생하는 경우를 반영하지 않아 현실적인 상황을 충분히 반영하지 못한다.
2. 유망한 노드만 포함한 상한 기반 분석
두 번째 방식은 가지치기를 고려하여, 유망한 노드만 포함한 상태공간트리의 노드 개수의 상한을 계산하는 것이다. 예를 들어, n-Queens 문제에서는 같은 열에 여왕을 배치할 수 없다는 제약을 통해 유망한 노드의 수를 줄일 수 있다. 첫 번째 여왕은 n개의 열 중 어느 곳에나 배치할 수 있고, 두 번째 여왕은 n−1개의 열, 세 번째는 n−2개의 열로 줄어들어, 유망한 노드의 총 개수는 1+n+n(n−1)+n(n−1)(n−2)+⋯+n!로 계산된다. 이 값은 대략 O(n!)의 시간복잡도를 나타내며, 이는 첫 번째 방법보다 훨씬 작은 값으로 현실적인 백트래킹 상황을 더 잘 반영한다. 하지만 이 분석 방법은 대각선을 점검하는 경우를 고려하지 않았다. 따라서 실제 유망한 마디의 수는 훨씬 더 작을 수 있다.
3. 실제 탐색된 노드 수 기반의 정확한 분석
세 번째 방식은 실제 탐색된 노드의 개수를 직접 세는 방식이다. 이는 실제로 알고리즘을 실행하여 상태공간트리에서 탐색된 노드의 수를 기록하는 방법이다. 이 방식은 가장 정확한 결과를 제공하지만, 이 또한 한계가 있다. 분석의 목적은 알고리즘을 실행하지 않고도 복잡도를 평가하는 데 있기 때문에, 이 방법은 진정한 분석 방법이 될 수없다. 몬테카를로 알고리즘과 같은 확률 알고리즘으로 복잡도를 추정하는 것은 가능하다.
void queens(index i) { // i번째 행 상태
index j; // 최상위 호출: queens(0)
if (promising(i)) {
if (i == n)
cout << col[1] through col[n]; // 해답 출력
else {
for (j = 1; j <= n; j++) { // (i+1)번째 행에 대해 열 검사
col[i + 1] = j; // i+1번째 행에 여왕말 배치
queens(i + 1); // 다음 행 탐색
}
}
}
}
bool promising(index i) { // i번째 행에서 여왕말의 유망성 검사
index k;
bool is_promising = true;
k = 1;
while (k < i && is_promising) {
if (col[i] == col[k] || abs(col[i] - col[k]) == i - k) {
is_promising = false; // 같은 열 또는 대각선에 다른 여왕말 존재
}
k++;
}
return is_promising;
}
Python 코드
def promising(i, n, col):
is_promising = True
# Check all previously placed queens
k = 1
while k < i and is_promising:
# Check if same column or on the same diagonal
if col[i] == col[k] or abs(col[i] - col[k]) == (i - k):
is_promising = False
k += 1
return is_promising
def nqueens(i, n, col):
# Check if the current placement is promising
if promising(i, n, col):
# If we have placed queens in all rows, print the solution
if i == n:
print("found=", col[1:])
else:
# Try placing a queen in every column of the next row (i+1)
for j in range(1, n+1):
col[i+1] = j
nqueens(i+1, n, col)
# Example 1
print("######Example 1######")
n = 4
col = [0] * (n + 1)
nqueens(0, n, col)
# Example 2 - Your Custom Case
print("######Example 2 #######")
# Let's try with n = 5
n = 5
col = [0] * (n + 1)
nqueens(0, n, col)
부분 집합의 합 구하기 (sum of subsets of problem)
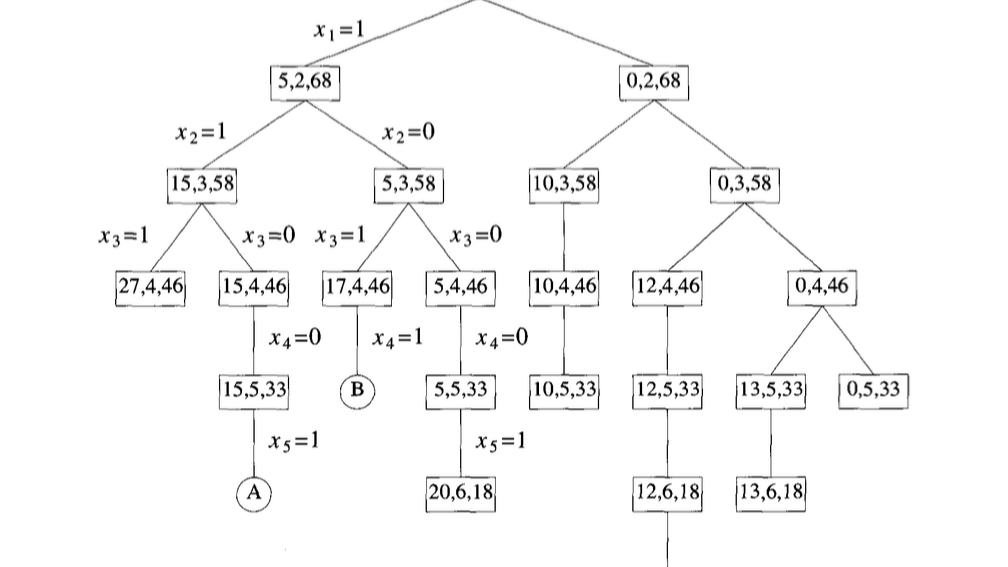
부분집합 합 구하기 문제는 주어진 집합에서 특정 합을 만족하는 부분집합을 찾는 문제다. 예를 들어, 집합 S = {1,4,6,8}와 목표 합 W=5가 주어졌을 때, 부분집합 {1,4}가 해답이 된다. 이 문제는 모든 가능한 부분집합을 탐색해야 하므로 탐색 공간이 매우 클 수 있지만, 백트래킹 알고리즘을 활용하면 불필요한 계산을 줄이고 효율적으로 해를 찾을 수 있다. 유망성 판단은 현재까지의 누적 무게와 남아 있는 아이템의 총합을 기준으로 이루어진다. 예를 들어, weight + total ≥ W 조건이 만족되지 않으면, 해당 노드는 유망하지 않은 상태로 판단되어 탐색을 중단한다.
알고리즘의 핵심은 재귀적으로 상태공간트리를 탐색하면서, 현재 노드가 목표 합 W를 만족하는지 확인하고, 만족하지 않으면 다음 노드로 진행하는 것이다. 각 노드에서 두 가지 선택을 한다: 현재 아이템을 포함하거나 포함하지 않는다. 포함하는 경우에는 누적 무게에 현재 아이템의 무게를 더하고, 포함하지 않는 경우에는 남은 아이템의 무게에서 현재 아이템의 무게를 제외한다. 이 과정을 반복하며, 모든 가능한 조합을 효율적으로 탐색한다. 이 알고리즘의 시간 복잡도는 최악의 경우 O(2^n)로, 모든 부분집합을 탐색해야 할 때 발생한다. 그러나 가지치기를 통해 실제 탐색해야 하는 노드의 수를 줄일 수 있다.
부분집합의 합 구하기 문제에서 백트래킹 효율성을 높이기 위해 아이템 무게를 오름차순으로 정렬한다. 이는 가장 가벼운 아이템을 추가했을 때도 조건을 충족하지 않으면 이후의 더 무거운 아이템을 탐색하지 않아도 되기 때문이다. 유망성 판단은 두 가지 조건으로 이루어진다. 첫째, 현재까지의 무게 합에 가장 가벼운 아이템을 더했을 때 를 초과하면 탐색 중단. 둘째, 현재 무게 합과 남은 아이템의 총 무게를 합해도 W에 도달하지 못하면 탐색을 종료한다. 이러한 판단은 불필요한 경로를 가지치기하여 탐색 효율을 높인다.
void sum_of_subsets(index i, int weight, int total) {
// 현재 상태가 유망한지 확인
if (promising(i)) {
// 현재 무게가 목표 무게와 같으면 해답 출력
if (weight == W) {
cout << include[1] through include[i]; // 선택된 부분집합 출력
} else {
// 다음 아이템 포함
include[i + 1] = 1;
sum_of_subsets(i + 1, weight + w[i + 1], total - w[i + 1]);
// 다음 아이템 포함하지 않음
include[i + 1] = 0;
sum_of_subsets(i + 1, weight, total - w[i + 1]);
}
}
}
bool promising(index i) {
// 현재 상태가 유망한지 판단
// (남은 아이템으로 목표 무게를 만족할 가능성이 있는지 확인)
return (weight + total >= W) && (weight == W || weight + w[i + 1] <= W);
}Python 코드
def promising(i, weight, total):
global n, W, w, include
if (weight + total >= W) and (weight == W or (i+1 <= n and weight + w[i+1] <= W)):
return True
return False
def sumofsubsets(i, weight, total):
global n, W, w, include
if promising(i, weight, total):
if weight == W:
print("found:", include[1:])
else:
if i+1 <= n:
include[i+1] = 1
sumofsubsets(i+1, weight + w[i+1], total - w[i+1])
include[i+1] = 0
sumofsubsets(i+1, weight, total - w[i+1])
print("######Example 1######")
n, W = 4, 13
w = [0, 3, 4, 5, 6]
include = [0] * (n + 1)
sumofsubsets(0, 0, sum(w[1:]))
print("######Example 2 #######")
n, W = 5, 10
w = [0, 2, 3, 4, 5, 6]
include = [0] * (n + 1)
sumofsubsets(0, 0, sum(w[1:]))복잡도 분석
부분집합의 합 구하기 문제에서 최악의 경우를 분석하기 위해 상태공간트리의 모든 노드 개수를 계산한다. 집합의 크기가 n일 때, 상태공간트리의 각 레벨에서 선택(포함/비포함)의 두 가지 경우가 있으므로, 레벨 i에서의 노드 개수는 2^i가 된다. 전체 상태공간트리는 루트 노드부터 시작해 n 레벨까지 확장되므로, 노드의 총 개수는 1로 계산되며, 이는 등비수열의 합 공식을 적용하여 2^{n+1} - 1로 표현된다.
따라서, 최악의 시간복잡도는 트리의 모든 노드를 탐색하는 경우에 해당하며, 이는 O(2^n)에 속한다. 이 복잡도는 가지치기(pruning) 없이 모든 가능한 부분집합을 탐색하는 상황을 반영하며, 문제의 크기 이 증가함에 따라 지수적으로 증가한다.
m - 색칠하기 문제 (m coloring problem)

m-색칠하기 문제(m-coloring problem)는 그래프에 개의 색을 사용해 인접한 정점이 같은 색을 가지지 않도록 색칠하는 문제다. 이 문제는 지도 색칠하기 문제의 일반화된 형태로, 지도에서 지역을 정점으로, 인접 관계를 간선으로 표현한 그래프에서 해결할 수 있다. 목표는 주어진 색의 수 으로 그래프의 모든 정점을 조건에 맞게 색칠하는 방법을 찾는 것이다.
그래프 색칠하기 (graph coloring)
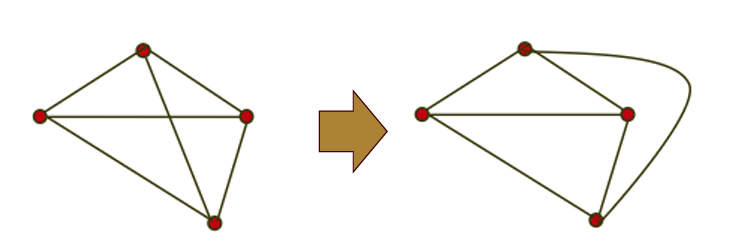
그래프 색칠하기는 그래프의 정점들에 색을 배정하는 문제로, 인접한 정점들에 동일한 색이 할당되지 않도록 하는 것이 목표다. 이 문제는 주로 지도 색칠 문제와 관련이 있다. 지도에서 각 지역을 그래프의 정점으로 표현하고, 서로 인접한 지역 간의 경계를 간선으로 나타냄으로써 지도를 그래프로 변환할 수 있다. 이렇게 변환된 그래프는 평면 그래프(planar graph)로, 이는 평면 상에서 간선들이 서로 엇갈리지 않게 그릴 수 있는 그래프를 의미한다.
평면 그래프는 모든 간선이 평면에서 교차하지 않도록 그릴 수 있기 때문에, 지도와 같은 물리적 경계를 수학적으로 분석하는 데 유용하다. 예를 들어, 지도에서 각 지역은 하나의 정점으로 표현되며, 두 지역이 인접해 있으면 해당 정점 사이에 간선을 추가한다. 모든 지도는 이러한 방식으로 평면 그래프로 변환할 수 있으며, 4색 정리에 따라 네 가지 색만으로 모든 지역을 구분하여 색칠할 수 있다. 하지만 비평면 그래프(nonplanar graph)의 경우, 간선들이 평면 상에서 반드시 교차해야 하기 때문에 4색 정리를 적용할 수 없다.
문제를 해결하기 위해 상태공간트리를 활용하며, 각 노드는 정점에 대한 색 배정을 나타낸다. 상태공간트리의 깊이는 번째 정점까지 색이 배정된 상태를 의미하며, 탐색 과정에서 조건을 위반하지 않는 색 배정을 유망한 상태로 간주한다. 조건을 위반하는 경우, 해당 경로는 가지치기(pruning)를 통해 탐색을 중단한다. 이러한 방식으로 백트래킹을 적용하여 탐색 범위를 줄인다.
m-색칠하기 문제의 백트래킹 알고리즘은 두 가지 주요 함수로 구성된다. 첫 번째는 m_coloring 함수로, 상태공간트리를 탐색하며 정점에 색을 배정한다. 이 함수는 i번째 정점에 대해 m개의 색을 순차적으로 시도하며, 조건을 만족하면 다음 정점으로 진행한다. 두 번째는 promising 함수로, 현재 정점에 배정된 색이 유망한지 판단한다. 이 함수는 현재 정점과 인접한 정점들 간의 색이 충돌하지 않는지 확인하여, 유망하지 않은 경우 탐색을 중단하게 한다.
bool m_coloring(int node) {
if (node > n) {
// 모든 노드를 성공적으로 색칠했음
print_solution();
return true;
}
for (int color = 1; color <= m; color++) {
if (is_promising(node, color)) { // 유망성 판단
colors[node] = color; // 현재 노드에 색칠
if (m_coloring(node + 1)) { // 다음 노드로 진행
return true; // 해답을 찾으면 종료
}
colors[node] = 0; // 백트래킹: 색 제거
}
}
return false; // 가능한 색깔 배치 실패
}
bool is_promising(int node, int color) {
for (int i = 1; i <= n; i++) { // 모든 인접 노드 확인
if (graph[node][i] && colors[i] == color) {
return false; // 인접 노드와 같은 색이면 유망하지 않음
}
}
return true; // 유망
}
void solve_m_coloring() {
if (!m_coloring(1)) {
print("No solution exists");
}
}Python 코드
def is_promising(node, color):
global W, vcolor, n
# node 노드에 color 색을 칠했을 때 인접 노드와 충돌하는지 검사
for i in range(1, n+1):
if W[node][i] == 1 and vcolor[i] == color:
return False
return True
def m_coloring(node, m):
global n, vcolor
# 모든 노드가 색칠 완료된 경우
if node > n:
print(vcolor[1:])
return True
# node 노드에 대하여 가능한 모든 색 할당 시도
for color in range(1, m+1):
if is_promising(node, color):
vcolor[node] = color
if m_coloring(node + 1, m):
# 해답을 찾았으므로 즉시 종료
return True
# 백트래킹
vcolor[node] = 0
return False
# Example 1
print("######Example 1######")
m = 3
n = 4
count = 0
vcolor = [0] * (n + 1)
W = [[0,0,0,0,0],
[0,0,1,1,1],
[0,1,0,1,0],
[0,1,1,0,1],
[0,1,0,1,0]]
mcoloring(0, m)
print("count =",count)
계산 복잡도 분석
이 알고리즘의 시간 복잡도는 최악의 경우 O(m^n)이며, 이는 모든 정점에 대해 개의 색을 할당하는 모든 조합을 탐색하는 경우에 해당한다. 하지만 백트래킹을 통해 유망하지 않은 경로를 가지치기함으로써 실제 탐색 범위를 대폭 줄일 수 있다. 탐색 범위의 크기는 그래프의 구조와 색의 수에 따라 달라지며, 간선이 많거나 사용할 수 있는 색이 적을수록 탐색이 더 제한적이 된다.
0 - 1 배낭 채우기 문제

0-1 배낭채우기 문제는 주어진 배낭의 용량을 초과하지 않으면서, 선택한 아이템들의 총 가치를 최대화하는 조합을 찾는 문제다. 각 아이템은 반드시 포함하거나 포함하지 않는 "0-1 선택"만 가능하다. 백트래킹은 이 문제를 해결하는 데 효과적인 기법으로, 상태공간트리를 이용해 모든 가능성을 탐색하면서 유망하지 않은 경로는 가지치기하여 탐색 효율을 높인다.

1. 상태 공간 트리 구성
트리의 각 노드는 특정 아이템을 선택하거나 선택하지 않음의 상태를 나타낸다. 트리의 루트는 아무것도 선택하지 않은 상태에서 시작한다.
- 왼쪽 자식 노드는 아이템을 선택한 상태를 나타내고, 오른쪽 자식 노드는 선택하지 않은 상태를 나타낸다.
- 모든 경로를 탐색하면 가능한 모든 아이템 조합을 살펴볼 수 있다.
2. 가지치기 (Pruning)
모든 노드를 탐색하지 않고, 유망하지 않은 경로를 미리 제거한다. 가지치기의 기준은 현재 노드에서 계산한 bound 값이다.
- bound는 이론적으로 현재 상태에서 얻을 수 있는 최대 이익이다.
- bound가 지금까지 발견된 최대 가치 maxprofit보다 작다면, 해당 경로는 탐색하지 않는다.
3. bound 계산
현재 노드에서 bound를 계산하는 방법은 다음과 같다:
- 현재까지 선택한 아이템의 가치 profit과 무게 weight를 계산한다.
- 남은 용량을 무게당 가치가 높은 순서로 채운다고 가정해 추가 이익을 계산한다.
- 추가된 이익을 더해 bound 값을 구한다.
예시
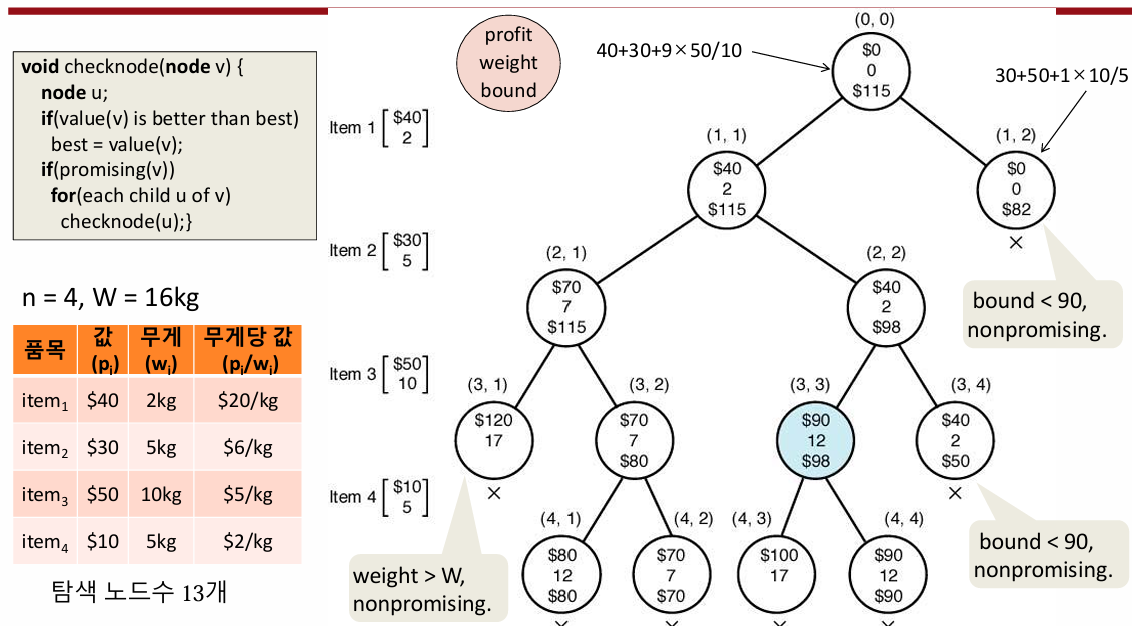
아이템 목록이 다음과 같이 주어졌다고 해보자
- 아이템 1: 가치 = 40, 무게 = 2, 무게당 가치 = 20
- 아이템 2: 가치 = 30, 무게 = 5, 무게당 가치 = 6
- 아이템 3: 가치 = 50, 무게 = 10, 무게당 가치 = 5
- 아이템 4: 가치 = 10, 무게 = 5, 무게당 가치 = 2
배낭의 최대 무게는 W=16이며, 아이템의 조합 중 가치를 최대로 만드는 집합을 구하는 것이 목표다.
(1) 초기 정렬
아이템은 무게당 가치를 기준으로 내림차순으로 정렬한다:
아이템 1 → 아이템 2 → 아이템 3 → 아이템 4
(2) 탐색 과정
- 루트 노드: 아무것도 선택하지 않은 상태에서 시작한다.
- 1번 아이템 선택 (profit = 40, weight = 2)
- 남은 용량: W−2=14
- bound 계산:
- 2번 아이템 선택 (profit = 30).
- 3번 아이템 선택 가능 (profit = 50).
- 4번 아이템 일부만 선택 가능.
- bound = 40+30+50=120
- bound가 maxprofit보다 크므로 탐색을 계속한다.
- 1번, 2번 아이템 선택 (profit = 70, weight = 7)
- 남은 용량: W−7=9
- bound 계산
- 3번 아이템 선택 가능 (profit = 50).
- bound = 70+50=120
- 계속 탐색한다
- 1번, 2번, 3번 아이템 선택 (profit = 120, weight = 17)
- 무게 초과로 유망하지 않음.
- 1번, 2번 선택 후 4번 선택 (profit = 80, weight = 12)
- 남은 용량: W−12=4
- 추가 선택 불가.
- 현재까지 maxprofit=80
최종 해답
탐색이 끝나면 발견된 최대 가치는 maxprofit=90이며, 최적의 아이템 조합은 [1, 2, 3]이다. 이 알고리즘은 모든 가능한 조합을 탐색하는 대신 가지치기를 통해 탐색 효율을 높이며, 최적의 해를 찾는다.
void knapsack(index i, int profit, int weight) {
if (weight <= W && profit > maxprofit) {
maxprofit = profit; // 최대 이익 갱신
numbest = i; // 현재까지 선택한 아이템 갯수 저장
bestset = include; // 현재 선택한 아이템 집합 저장
}
if (promising(i)) { // 현재 상태가 유망한 경우 탐색 진행
include[i+1] = 1; // i+1번째 아이템 선택
knapsack(i+1, profit + p[i+1], weight + w[i+1]);
include[i+1] = 0; // i+1번째 아이템 선택하지 않음
knapsack(i+1, profit, weight);
}
}
bool promising(index i) {
index j, k;
int totweight;
float bound;
if (weight >= W) return false; // 배낭 무게 한도 초과 시 유망하지 않음
j = i + 1;
bound = profit;
totweight = weight;
// 남은 아이템을 추가하며 bound 계산
while (j <= n && totweight + w[j] <= W) {
totweight = totweight + w[j];
bound = bound + p[j];
j++;
}
k = j;
// 남은 공간에 아이템 일부 추가 (무게당 가치 고려)
if (k <= n) {
bound = bound + (W - totweight) * (p[k] / w[k]);
}
return bound > maxprofit; // bound가 현재 maxprofit보다 크면 유망
}
Python 코드
def promising(i, weight, profit):
global n, W, w, p, maxprofit
if weight >= W:
return False
total_weight = weight
bound = profit
j = i + 1
while j <= n and total_weight + w[j] <= W:
total_weight += w[j]
bound += p[j]
j += 1
if j <= n:
bound += (W - total_weight) * (p[j] / w[j])
return bound > maxprofit
def knapsack(i, weight, profit):
global n, W, w, p, bestset, include, maxprofit
if weight <= W and profit > maxprofit:
maxprofit = profit
for k in range(1, n + 1):
bestset[k] = include[k]
if i < n and promising(i, weight, profit):
include[i + 1] = 1
knapsack(i + 1, weight + w[i + 1], profit + p[i + 1])
include[i + 1] = 0
knapsack(i + 1, weight, profit)
# Example 1
print("######Example 1######")
n, W = 4, 16
w = [0] + [2, 5, 10, 5]
p = [0] + [40, 30, 50, 10]
bestset, include = [0] * (n + 1), [0] * (n + 1)
maxprofit = 0
knapsack(0, 0, 0)
print("maxprofit =", maxprofit)
print("bestset =", bestset)
# Example 2
print("######Example 2 #######")
n, W = 5, 15
w = [0] + [1, 3, 4, 7, 8]
p = [0] + [5, 6, 10, 12, 13]
bestset, include = [0] * (n + 1), [0] * (n + 1)
maxprofit = 0
knapsack(0, 0, 0)
print("maxprofit =", maxprofit)
print("bestset =", bestset)
2. 분기 한정법 (Branch - and - Bound)

최소화 문제와 최대화 문제는 최적화 문제의 두 가지 대표적인 유형이다. 최소화 문제는 주어진 제약 조건 내에서 목표 함수의 값을 가능한 가장 작게 만드는 것이 목적이다. 예를 들어, 특정 경로에서 이동 거리를 최소화하거나 생산 비용을 최소화하는 문제들이 있다. 이러한 문제를 해결하기 위해서는 트리의 각 노드에서 하한(lower bound)을 계산하여 탐색을 이어갈지 결정한다. 현재까지 발견된 최소값보다 작은 가능성이 있다면 탐색을 계속하지만, 그렇지 않다면 가지치기를 통해 탐색을 종료한다. 이는 불필요한 계산을 줄이고 효율성을 높이는 데 중요한 역할을 한다.
반면, 최대화 문제는 목표 함수의 값을 가능한 가장 크게 만드는 것을 목적으로 한다. 예를 들어, 제한된 자원 내에서 최대 이익을 얻거나, 배낭 채우기 문제에서 최대 가치를 만드는 조합을 찾는 것이 이에 해당한다. 이 문제에서는 상한(upper bound)을 계산하여 탐색 여부를 결정한다. 상한이 현재까지의 최대값보다 크면 탐색을 계속하고, 작거나 같다면 해당 경로를 더 이상 확장하지 않는다. 최대화 문제는 이익이나 가치를 극대화하려는 상황에서 자주 나타나며, 효율적인 탐색 전략이 중요하다.
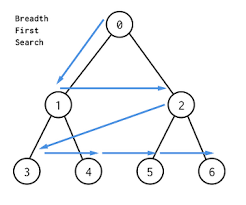
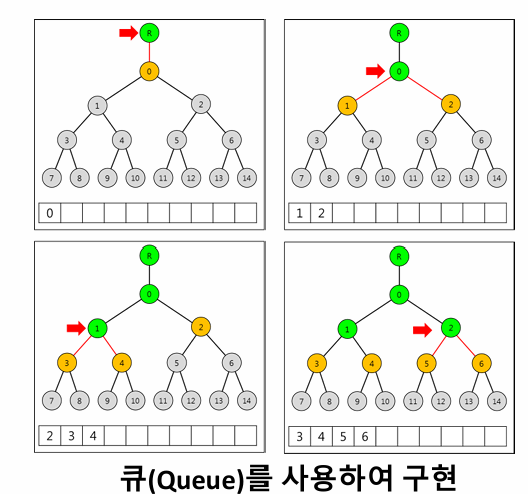
너비우선검색(Breadth-First Search, BFS)은 트리나 그래프에서 탐색을 수행할 때 사용하는 알고리즘으로, 각 노드를 계층적으로 방문한다. 탐색은 뿌리(root) 노드에서 시작하며, 해당 노드의 모든 자식 노드를 차례로 방문한 후, 그다음 깊이로 내려가서 또다시 모든 자식 노드를 방문하는 방식으로 진행된다. 즉, 특정 깊이의 모든 노드를 탐색한 후에야 다음 깊이로 이동하기 때문에, 탐색이 진행되는 동안 모든 노드가 특정 깊이에 따라 균등하게 확장된다.
이 알고리즘은 일반적으로 큐(Queue) 자료구조를 사용하여 구현된다. 큐는 선입선출(FIFO) 방식으로 작동하며, 방문할 노드가 삽입된 순서대로 처리된다. BFS는 노드 방문 순서를 엄격히 유지하며, 먼저 탐색해야 할 노드가 항상 가장 먼저 처리되도록 보장한다. 탐색 과정은 다음과 같다: 첫 번째로 뿌리 노드를 큐에 추가하고, 큐에서 노드를 하나씩 제거하며 해당 노드의 자식 노드를 큐에 추가한다. 이 과정을 큐가 빌 때까지 반복하면 탐색이 완료된다.
너비우선검색의 주요 특징은 최단 경로 탐색에 적합하다는 것이다. 가중치가 없는 그래프에서 BFS를 사용하면 특정 시작점에서 다른 모든 노드까지의 최단 경로를 정확히 구할 수 있다. 하지만, BFS는 노드를 계층적으로 방문하기 때문에 탐색 공간이 넓거나 노드가 많을 경우 많은 메모리를 소비할 수 있다는 단점이 있다. 이러한 이유로 BFS는 비교적 노드 수가 적거나, 최단 경로 탐색이 중요한 문제에 적합하다. 이 알고리즘은 분기한정법과 같은 최적화 문제에도 활용되며, 탐색 순서를 체계적으로 유지하여 문제를 효율적으로 해결한다.
void breadth_first_search(tree T) {
// 큐 선언: BFS에서는 노드들을 관리하기 위해 큐를 사용
queue_of_node Q;
// 노드 선언: 현재 탐색 중인 노드(v)와 자식 노드(u)를 표현
node u, v;
// 큐 초기화: 탐색을 시작하기 전에 큐를 초기화
initialize(Q);
// 트리의 루트 노드를 탐색의 시작점으로 설정
v = root of T;
// 루트 노드를 방문 (예: 데이터 출력, 처리 등)
visit v;
// 루트 노드를 큐에 추가: BFS는 큐에 노드를 추가하며 탐색 진행
enqueue(Q, v);
// 큐가 비어 있지 않은 동안 반복
while (!empty(Q)) {
// 큐에서 노드를 꺼냄: FIFO 방식으로 가장 먼저 들어온 노드가 처리됨
dequeue(Q, v);
// 현재 노드(v)의 모든 자식 노드(u)에 대해 반복
for (each child u of v) {
// 자식 노드(u)를 방문
visit u;
// 자식 노드를 큐에 추가: 이후 탐색을 위해 큐에 저장
enqueue(Q, u);
}
}
}
분기한정법(Branch-and-Bound)은 상태 공간 트리를 구성하여 가능한 해를 체계적으로 탐색하는 기법이다. 이 알고리즘의 핵심은 각 노드에서 해답의 가능성을 평가하기 위해 한계값(bound)을 계산하는 것이다. 한계값은 해당 경로를 통해 얻을 수 있는 해답의 최대 또는 최소값을 나타내며, 이를 바탕으로 탐색을 계속할지 가지치기(pruning)할지를 결정한다.
탐색 과정에서 노드가 유망(promising)하다면, 즉 한계값이 현재까지의 최적 해보다 더 좋은 가능성을 보인다면, 해당 노드의 자식 노드를 탐색한다. 반면, 노드가 유망하지 않다면 해당 경로는 더 이상 확장하지 않고 탐색을 중단한다. 이로써 불필요한 계산을 줄이고 효율성을 높일 수 있다. 분기한정법은 탐색 순서에 구애받지 않기 때문에 깊이우선검색(DFS), 너비우선검색(BFS), 최고우선검색(Best-First Search) 등 다양한 탐색 전략과 결합될 수 있다.
백트래킹과 분기한정법은 상태 공간을 탐색하는 기법이지만, 목적과 가지치기 기준에서 차이가 있다. 백트래킹은 조건을 만족하는 해를 찾는 데 중점을 두며, 예를 들어 미로 찾기에서 막힌 길이나 이미 방문한 길을 만나면 되돌아가 다른 경로를 시도한다. 반면, 분기한정법은 최적의 해를 찾는 데 초점이 있으며, 예를 들어 최단 경로 문제에서 현재 경로의 최소 거리가 이미 발견된 최단 거리보다 길 가능성이 있다면 해당 경로를 아예 탐색하지 않는다. 따라서 백트래킹은 조건을 만족하는 해를, 분기한정법은 가장 좋은 해를 목표로 한다.
void breadth_first_branch_and_bound(state_space_tree T, number& best) {
// 큐 선언: 노드를 저장하고 탐색을 관리
queue_of_node Q;
// 노드 선언: 현재 노드(v)와 자식 노드(u)를 표현
node u, v;
// 큐 초기화: 탐색 준비
initialize(Q); // Q는 빈 큐로 초기화
// 루트 노드를 가져와 탐색의 시작점으로 설정
v = root of T;
// 루트 노드를 큐에 추가
enqueue(Q, v);
// 초기 최적값(best)을 루트 노드의 값으로 설정
best = value(v);
// BFS 방식으로 트리 탐색
while (!empty(Q)) {
// 큐에서 노드를 꺼냄
dequeue(Q, v);
// 현재 노드(v)의 자식 노드(u)를 순회
for (each child u of v) {
// u의 값이 현재 최적값(best)보다 더 나으면 업데이트
if (value(u) is better than best) {
best = value(u);
}
// u의 bound가 최적값(best)보다 더 나으면 탐색 대상으로 간주
if (bound(u) is better than best) {
enqueue(Q, u); // u를 큐에 추가하여 탐색 계속
}
// 그렇지 않으면 해당 경로는 가지치기(Pruning)
}
}
}
0-1 배낭 채우기 분기한정 너비우선검색

0-1 배낭 채우기 분기한정 너비우선검색은 분기한정법(Branch-and-Bound)을 사용하여 배낭 문제를 해결하는 알고리즘으로, 너비우선검색(Breadth-First Search, BFS) 방식을 적용한다. 이 알고리즘은 상태 공간 트리의 각 노드를 계층적으로 탐색하며, 각 노드에서 현재 선택된 아이템의 이익과 무게를 계산하고, 추가적인 이익 가능성을 나타내는 한계값(bound)을 구한다. 탐색 중, 현재 노드의 무게가 배낭의 용량(W)을 초과하거나, 한계값이 지금까지 발견된 최대 이익(maxprofit)보다 낮으면 해당 경로를 가지치기하여 효율성을 높인다.
구체적으로, 이 알고리즘은 큐(Queue)를 사용하여 노드들을 저장하며, 뿌리(root) 노드에서 시작하여 각 노드의 자식 노드를 생성해 큐에 추가한다. 각 노드에서 아이템을 포함하거나 포함하지 않는 두 가지 경우를 고려하며, 포함 여부에 따라 이익과 무게를 갱신한다. 이때, 갱신된 상태가 유망(promising)할 경우에만 큐에 추가하여 탐색을 이어간다. BFS 방식이므로 먼저 특정 깊이의 모든 노드를 탐색한 뒤, 그다음 깊이로 이동한다.
0-1 배낭 채우기 문제에서 이 알고리즘은 최적의 해를 보장하면서도, 유망하지 않은 경로를 가지치기함으로써 탐색 공간을 줄인다. 예를 들어, 아이템 4개와 용량 16kg의 배낭 문제에서, 너비우선검색을 통해 가능한 모든 조합을 고려하되, 불필요한 경로를 제거하여 최적의 이익을 찾는다. 이를 통해 최대 이익과 함께 최적의 아이템 조합을 효율적으로 도출할 수 있다.
void knapsack2(int n, const int p[], const int w[], int W, int& maxprofit) {
queue_of_node Q;
node u, v;
initialize(Q);
v.level = 0;
v.profit = 0;
v.weight = 0;
maxprofit = 0;
enqueue(Q, v);
while (!empty(Q)) {
dequeue(Q, v);
// "아이템 포함" 자식 노드 생성
u.level = v.level + 1;
u.weight = v.weight + w[u.level];
u.profit = v.profit + p[u.level];
if (u.weight <= W && u.profit > maxprofit) {
maxprofit = u.profit;
}
if (bound(u) > maxprofit) {
enqueue(Q, u);
}
// "아이템 미포함" 자식 노드 생성
u.weight = v.weight;
u.profit = v.profit;
if (bound(u) > maxprofit) {
enqueue(Q, u);
}
}
}float bound(node u) {
index j, k;
int totweight;
float result;
// 배낭 용량 초과 시 0 반환
if (u.weight >= W)
return 0;
else {
result = u.profit; // 현재 이익 초기화
j = u.level + 1;
totweight = u.weight;
// 남은 공간에 아이템을 가능한 한 채움
while (j <= n && totweight + w[j] <= W) {
totweight = totweight + w[j];
result = result + p[j];
j++;
}
// 마지막 아이템의 일부를 추가
k = j;
if (k <= n)
result = result + (W - totweight) * p[k] / w[k];
return result;
}
}
분기한정 가지치기로 최고우선검색 (Best-First Search; BestFS)

최고우선검색(Best-First Search; BestFS)은 분기한정법에서 사용되는 탐색 방법으로, 가장 높은 한계치(bound)를 가진 노드를 우선적으로 탐색하여 최적의 해를 빠르게 찾는 전략이다. 이 방법은 우선순위 큐(priority queue)를 활용하여 유망한 노드들을 관리하며, 최적화 문제를 해결할 때 매우 효과적이다.
1. 주어진 노드의 모든 자식 노드를 검색한 후
2. 유망하면서 확장되지 않은(unexpanded) 노드를 살펴보고
3. 그 중에서 가장 좋은한계치(bound)를 가진 노드를 확장한다.
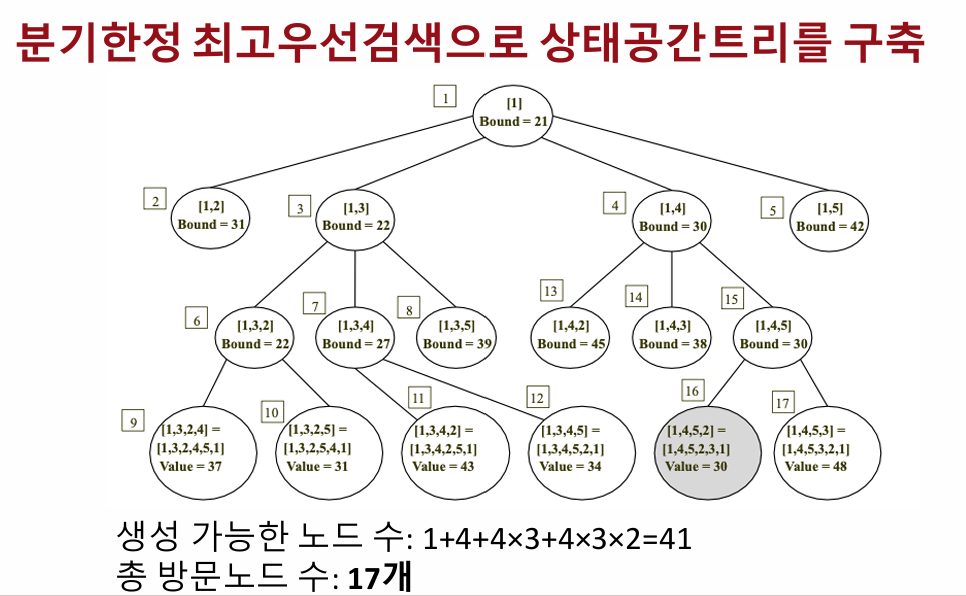
최고우선검색의 핵심은 탐색 과정에서 현재 가장 가능성이 높은 노드(최고 bound)를 우선적으로 탐색하는 것이다. bound란, 해당 노드에서 앞으로 얻을 수 있는 최적의 이익을 추정한 값이다. 따라서, bound가 낮은 노드는 더 이상 탐색하지 않고 가지치기(pruning)하여 탐색의 효율을 높인다. 우선순위 큐는 이러한 bound 값을 기준으로 정렬하여 탐색 우선순위를 관리한다.
최고우선검색은 탐색해야 할 노드의 수를 줄이면서도 최적의 해를 보장하는 효율적인 방법이다. 예를 들어, 동일한 문제를 백트래킹(DFS)으로 해결할 경우 13개의 노드를, 너비우선검색(BFS)으로 해결할 경우 17개의 노드를 탐색해야 한다. 반면, BestFS는 단 11개의 노드만 탐색해 최적의 해를 찾아낸다. 이는 가장 유망한 노드부터 탐색하여 불필요한 경로를 빠르게 가지치기하기 때문이다.
void best_first_branch_and_bound(state_space_tree T, number& best) {
priority_queue_of_node PQ; // 우선순위 큐 선언 (노드들의 bound를 기준으로 우선순위 관리)
node u, v; // 탐색 중 사용할 노드 변수 선언
initialize(PQ); // 우선순위 큐를 빈 상태로 초기화
v = root of T; // 루트 노드를 탐색의 시작점으로 설정
best = value(v); // 초기 최적값(best)을 루트 노드의 값으로 설정
insert(PQ, v); // 루트 노드를 우선순위 큐에 삽입
while (!empty(PQ)) { // 우선순위 큐가 비어 있지 않은 동안 반복
remove(PQ, v); // 우선순위 큐에서 최고 bound를 가진 노드 v를 꺼냄
if (bound(v) is better than best) { // 현재 노드의 bound가 최적값(best)보다 클 경우에만 탐색
for (each child u of v) { // v의 모든 자식 노드를 확인
if (value(u) is better than best) {
best = value(u); // 자식 노드 u의 값이 기존 최적값보다 크다면 최적값 갱신
}
if (bound(u) is better than best) {
insert(PQ, u); // 자식 노드 u의 bound가 최적값보다 클 경우, 큐에 추가
}
}
}
// 유망하지 않은 노드(v)의 자식들은 더 이상 탐색하지 않음 (가지치기)
}
}
0-1 배낭 채우기 분기한정 최고우선검색(Best-First Search, BestFS)

분기 한정 최고 우선 검색은 0-1 배낭 문제를 해결하기 위한 탐색 알고리즘으로, 분기한정법(Branch-and-Bound)과 최고우선검색 전략을 결합하여 최적의 해를 효율적으로 찾아낸다. 이 알고리즘은 상태 공간 트리를 탐색하면서 한계값(bound)을 기준으로 가장 유망한 노드를 우선적으로 확장하며, 우선순위 큐(priority queue)를 활용해 한계값이 가장 높은 노드부터 처리한다.
탐색은 루트 노드에서 시작하여, 노드가 유망(promising)하면 두 가지 경우(아이템 포함, 아이템 미포함)를 고려한 자식 노드를 생성한다. 각 노드에서는 현재까지의 이익(profit)과 무게(weight)를 갱신하고, 가능한 최대 이익을 계산하는 한계값(bound)을 구한다. 한계값이 현재까지의 최대 이익(maxprofit)보다 크면 해당 노드를 우선순위 큐에 추가해 탐색을 이어가고, 작으면 가지치기(pruning)를 통해 탐색을 중단한다. 이러한 과정을 반복하며 큐가 비게 되면 탐색이 종료되고 최적의 해가 도출된다.
예를 들어, 0-1 배낭 문제에서 아이템의 무게와 가치를 기준으로 배낭의 용량을 초과하지 않는 범위 내에서 최대 이익을 찾는 경우, BestFS는 유망하지 않은 경로를 일찍 가지치기하여 불필요한 계산을 줄인다. 이 알고리즘은 탐색 공간이 큰 문제에서 특히 유용하며, 너비우선검색(BFS)보다 더 적은 노드를 탐색하면서 최적의 해를 빠르게 찾아낸다. 이를 통해 효율성을 극대화하며, 최적화 문제 해결에 적합한 기법으로 활용된다.
void knapsack3(int n, const int p[], const int w[], int W, int& maxprofit) {
// 우선순위 큐(Priority Queue) 선언
priority_queue_of_node PQ;
node u, v; // 노드 선언 (현재 노드 v와 자식 노드 u)
initialize(PQ); // 우선순위 큐를 초기화
v.level = 0; // 루트 노드 초기화
v.profit = 0; // 현재까지의 이익 초기화
v.weight = 0; // 현재까지의 무게 초기화
maxprofit = 0; // 최적의 이익 초기화
v.bound = bound(v); // bound 함수로 현재 노드의 예상 최대 이익 계산
insert(PQ, v); // 루트 노드를 큐에 삽입
// 우선순위 큐가 비어있지 않은 동안 탐색
while (!empty(PQ)) {
remove(PQ, v); // 큐에서 bound 값이 가장 큰 노드 v를 추출
if (v.bound > maxprofit) { // 현재 노드가 유망한 경우에만 탐색
// 자식 노드 1: 현재 아이템 포함
u.level = v.level + 1; // 자식 노드의 레벨 증가
u.weight = v.weight + w[u.level]; // 현재 아이템의 무게 추가
u.profit = v.profit + p[u.level]; // 현재 아이템의 이익 추가
// 자식 노드가 배낭 용량(W)을 초과하지 않고, 이익이 최대값을 초과하면 갱신
if (u.weight <= W && u.profit > maxprofit) {
maxprofit = u.profit; // 최적의 이익 갱신
}
u.bound = bound(u); // 현재 노드에서의 예상 최대 이익 계산
if (u.bound > maxprofit) {
insert(PQ, u); // 유망한 경우 자식 노드를 큐에 삽입
}
// 자식 노드 2: 현재 아이템 미포함
u.weight = v.weight; // 무게 유지
u.profit = v.profit; // 이익 유지
u.bound = bound(u); // 예상 최대 이익 계산
if (u.bound > maxprofit) {
insert(PQ, u); // 유망한 경우 자식 노드를 큐에 삽입
}
}
// 현재 노드가 유망하지 않으면 가지치기(Pruning)
}
}외판원 문제 (Traveling Salesman Problem)

외판원 문제(Traveling Salesman Problem, TSP)는 한 정점에서 출발하여 다른 모든 정점을 정확히 한 번씩만 방문하고 다시 출발점으로 돌아오는 경로 중에서, 가장 짧은 총 길이를 가지는 경로를 찾는 것이 목표다. 이때 사용되는 그래프는 음이 아닌 가중치를 가진 방향 그래프 또는 비방향 그래프로 표현된다.

외판원 문제는 해밀턴 순환(Hamiltonian Cycle)과 밀접한 관련이 있다. 해밀턴 순환이란 모든 정점을 정확히 한 번씩 방문하고 출발점으로 되돌아오는 경로를 말한다. 외판원 문제는 이러한 해밀턴 순환 중에서도 가중치의 합이 가장 작은 최적 경로를 찾는 문제다. 외판원 문제의 난이도는 가능한 경로의 조합 수에 기인한다. 정점의 개수가 일 때, 가능한 경로의 수는 (n−1)!로 급격히 증가한다. 예를 들어, 정점이 5개라면 가능한 경로는 24개, 정점이 10개라면 경로는 362,880개에 이른다. 이러한 조합 폭발로 인해, 단순히 모든 가능한 경로를 탐색하여 최적 경로를 찾는 방식은 효율적이지 않다.
이를 해결하기 위해 분기한정법(Branch-and-Bound)이 사용된다. 상태공간트리를 활용하여 가능한 경로를 체계적으로 탐색한다. 각 노드는 현재까지의 경로를 나타내며, 경로의 하한(Bound)을 계산하여 최적 경로가 될 가능성이 없는 경로는 탐색을 배제한다. 이렇게 함으로써 탐색 공간을 줄이고 효율적으로 최적 경로를 찾을 수 있다. 상태공간트리에서 경로의 하한은 현재까지의 경로 길이와 앞으로 추가될 경로의 최소 비용 합으로 계산된다. 예를 들어, 특정 경로에서 출발 정점으로 돌아오기까지 필요한 최소 비용을 계산하여 하한을 설정하고, 이 값이 이미 발견된 최적 경로보다 크다면 해당 경로를 배제한다. 이러한 방식을 반복하여 최적 경로를 찾는다. 분기한정법은 상태공간트리를 구축하고 노드를 탐색하면서, 하한 값이 최소 경로 길이보다 작은 노드만 확장한다. 이를 통해 불필요한 경로 확장을 방지하며, 최적 경로를 효율적으로 탐색할 수 있다.
상태공간트리 구축방법
외판원 문제를 해결하기 위해 상태공간트리를 구축하는 방법은 분기한정법의 핵심 과정이다. 이 트리는 가능한 모든 일주 여행 경로를 체계적으로 탐색하기 위한 구조로 사용된다. 상태공간트리의 각 노드는 현재까지 선택된 여행 경로를 나타내며, 이를 단계별로 확장하여 최적 경로를 찾는다.
트리 구축은 뿌리(root) 노드에서 시작된다. 뿌리 노드는 출발 정점에서 시작하는 경로를 나타내며, 초기 상태에서는 단순히 [1]과 같은 형태로 표현된다. 이후 각 노드는 다음에 방문할 수 있는 정점을 자식 노드로 확장한다. 예를 들어, 뿌리 노드 [1]에서 수준 1로 확장하면 [1,2], [1,3], ..., [1,n]과 같이 모든 가능한 다음 경로를 생성한다.
이 과정은 자식 노드에서도 동일하게 반복된다. 예를 들어, 노드 [1,2]는 다시 [1,2,3], [1,2,4], ..., [1,2,n]과 같은 하위 노드로 확장된다. 이처럼 모든 가능한 경로를 탐색하기 위해 노드가 확장되며, 잎(leaf) 노드에 도달할 때는 완전한 일주 여행 경로가 형성된다.
이 과정에서 모든 노드를 끝까지 확장하지 않아도 되는 경우가 있다. 잎 노드에서 마지막 남은 정점과 출발 정점으로 돌아가는 경로는 자동으로 결정되기 때문이다. 따라서 특정 노드에서 경로가 거의 완성된 상태라면 추가 확장을 중단하고 경로를 완성할 수 있다. 예를 들어, [1,2,3,4]까지 경로가 형성된 경우, 마지막 정점 [5]와 출발 정점 [1]을 연결하여 [1,2,3,4,5,1]로 바로 완성할 수 있다.
상태공간트리 구축에서 중요한 점은 각 노드에서 경로의 비용 하한(Bound)을 계산하여 탐색의 효율성을 높이는 것이다. 하한은 현재까지 선택된 경로와 남은 경로 중 최소 비용의 합으로 계산되며, 이 값이 이미 발견된 최적 경로보다 크다면 해당 경로를 확장하지 않고 배제한다. 이렇게 하면 불필요한 경로 탐색을 줄이고 최적 경로를 더 빠르게 발견할 수 있다.
요약하면, 상태공간트리 구축은 뿌리 노드에서 시작하여 가능한 모든 경로를 체계적으로 탐색하고, 불필요한 경로를 배제하여 탐색 공간을 줄이는 방식으로 이루어진다. 이 과정은 외판원 문제의 최적 경로를 효율적으로 찾기 위한 기반이 된다.
여행 길이의 하한(Bound) 구하기
여행길이의 하한(Bound)을 구하는 과정은 현재까지 선택한 경로를 기준으로 남은 경로의 최소 비용을 추정하여, 해당 경로가 최적 경로가 될 가능성이 있는지 판단하는 기준을 제공한다. 간단한 예시를 통해 이를 설명한다. 예를 들어, 5개의 정점 v1,v2,v3,v4,v5가 주어진 그래프에서, 각 정점 간의 여행 비용은 다음과 같다고 가정하자:

이 과정은 그래프의 모든 정점을 고려하며 남은 경로에서 최적의 최소 비용을 추정한다. 만약 이 하한이 이미 발견된 최적 경로의 길이보다 크다면, 현재 경로는 탐색하지 않고 배제할 수 있다. 위 예시는 단순한 5개의 정점으로 구성되어 있지만, 더 큰 그래프에서도 동일한 원리가 적용된다.
결론적으로, 하한을 구하는 과정은 현재까지의 경로 비용과 남은 경로의 최소 비용을 더하여 가능한 최적 경로의 최솟값을 추정하는 것이다. 이를 통해 탐색 공간을 줄이고 효율적으로 최적 경로를 찾을 수 있다.
// 외판원 문제를 푸는 분기한정 알고리즘
void travel(int n, const number W[][], ordered_set& opttour, number& minlength) {
// 우선순위 큐와 노드 정의
priority_queue_of_node PQ;
node u, v;
// 우선순위 큐 초기화
initialize(PQ);
// 출발 정점 설정
v.level = 0;
v.path = [1]; // 첫째 정점을 출발점으로 설정
v.bound = bound(v, n, W); // 첫 노드의 하한 계산
minlength = INFINITY; // 초기 최소 경로 길이를 무한대로 설정
insert(PQ, v); // 큐에 첫 노드 삽입
// 큐가 비어있지 않을 동안 탐색 반복
while (!empty(PQ)) {
remove(PQ, v); // 최고 우선순위(최소 하한) 노드 제거
if (v.bound < minlength) { // 현재 노드의 하한이 최소 경로 길이보다 작을 경우 탐색
u.level = v.level + 1; // u를 v의 자식 노드로 설정
// 다음 정점 탐색
for (all i such that 2 <= i <= n && i is not in v.path) {
u.path = v.path; // v의 경로를 복사
put i at the end of u.path; // 현재 정점 추가
if (u.level == n - 2) { // 모든 정점을 방문할 경우 확인
put index of only vertex not in u.path at the end of u.path; // 남은 정점 추가
put 1 at the end of u.path; // 마지막에 출발점 추가
if (length(u.path, W) < minlength) { // 현재 경로의 길이가 최소 길이보다 짧은지 확인
minlength = length(u.path, W); // 최소 경로 업데이트
opttour = u.path; // 최적 경로 업데이트
}
} else {
u.bound = bound(u, n, W); // 자식 노드의 하한 계산
if (u.bound < minlength) { // 하한이 최소 경로 길이보다 작으면 큐에 삽입
insert(PQ, u);
}
}
}
}
}
}
// 노드의 하한(bound) 계산 함수
float bound(node v, int n, const number W[][]) {
number lower = length(v.path, W); // 현재 경로의 길이 계산
// 모든 정점에 대해 최소 비용을 계산
for (int i = 1; i <= n; ++i) {
if (hasOutgoing(i, v.path)) continue; // 이미 경로에서 나간 정점은 스킵
number minimum = INFINITY; // 최소 비용 초기화
for (int j = 1; j <= n; ++j) {
if (i == j) continue; // 동일 노드 방문 스킵
if (j == 1 && i == v.path[v.level]) continue; // 마지막 노드가 시작 노드로 돌아가는 경우 스킵
if (hasIncoming(j, v.path)) continue; // 이미 경로에 포함된 노드는 스킵
minimum = min(minimum, W[i][j]); // 최소 비용 갱신
}
lower += minimum; // 최소 비용 누적
}
return lower; // 계산된 하한 반환
}
// 경로의 길이(length) 계산 함수
float length(ordered_set path, const number W[][]) {
// 경로 상의 모든 정점 간의 거리 합을 계산
float total_length = 0;
for (int i = 0; i < path.size() - 1; ++i) {
total_length += W[path[i]][path[i + 1]];
}
return total_length;
}
'Computer Scinece > Programming Principles' 카테고리의 다른 글
| Programming Principles [8] : 정렬 알고리즘 (Sortion Algorithms) (0) | 2024.12.03 |
|---|---|
| Programming Principles [6] : 최적화 알고리즘 (Optimization Algorithms) (1) | 2024.09.18 |
| Programming Principles [5] : 재귀 알고리즘 (Recursive Algorithm) (0) | 2024.09.18 |
| Programming Principles [4] : 자료 구조 (Data Structures) (0) | 2024.09.18 |
| Programming Principles [3]: 데이터 추상화와 리스트 (Data Structures & List) (1) | 2024.09.18 |
