
계산 복잡도 분석은 문제를 해결할 수 있는 모든 알고리즘의 효율성을 평가하고, 해당 문제의 하한(Ω)을 결정하는 과정이다. 예를 들어, 행렬 곱셈 문제의 일반 알고리즘은 Θ(n3)의 시간복잡도를 가지며, 개선된 알고리즘으로는 쉬트라쎈 알고리즘 (Θ(n2.81))과 위노그라드 알고리즘 (Θ(n2.38))이 존재한다. 하지만, 이 문제의 계산 복잡도 하한은 Θ(n2)로 알려져 있으나, 이만큼 효율적인 알고리즘은 아직 발견되지 않았다. 이는 하한보다 효율적인 알고리즘을 만드는 것이 불가능함을 의미하며, 예를 들어 3×3 행렬 곱셈에서는 기존 방식으로는 27번의 연산이 필요하지만, 개선된 알고리즘은 이를 줄일 수 있음을 보여준다.
계산 복잡도에서 문제의 복잡도 하한이 Ω(f(n))인 경우, 시간 복잡도가 Θ(f(n))인 알고리즘을 만드는 것이 목표다. 복잡도 하한보다 낮은 알고리즘을 만드는 것은 불가능하며, 예로 정렬 문제에서 교환 정렬은 Θ(n2), 합병 정렬은 Θ(nlogn)의 시간 복잡도를 가진다. 정렬 문제의 계산 복잡도 하한은 Ω(nlogn)로 증명되었고, 합병 정렬은 이 하한에 도달한 효율적인 알고리즘의 대표적 사례다. 이는 정렬 문제의 최적 효율을 실현하는 알고리즘이 존재함을 보여준다.
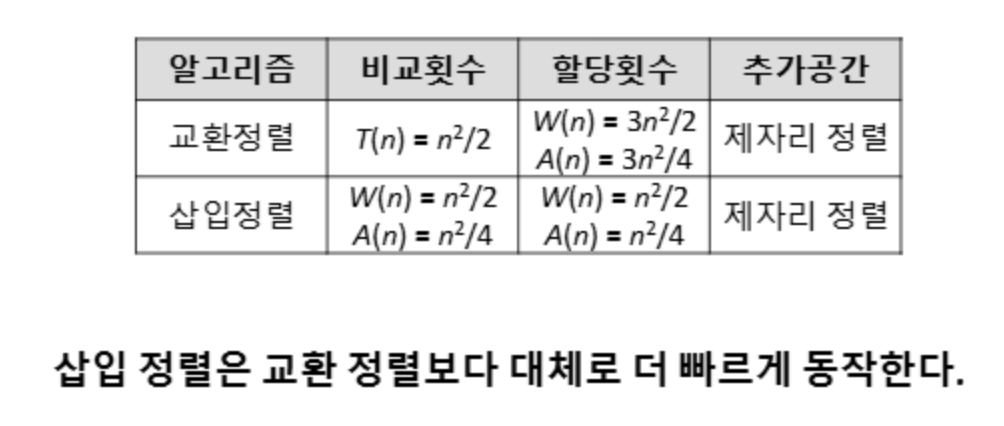
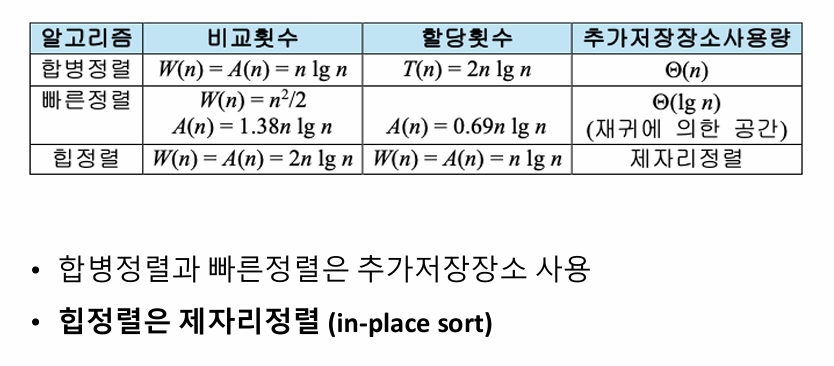
알고리즘의 효율성은 키의 비교 횟수와 데이터의 할당(assignment) 횟수를 기준으로 세부적으로 분석된다. 예를 들어, 교환 연산의 경우 한 번의 교환이 이루어지더라도 실제로는 세 번의 데이터 할당 작업이 필요하다. 데이터의 크기가 커질수록 이러한 할당 작업에 소요되는 시간이 증가하므로, 단순한 연산 횟수 외에도 데이터 크기에 따른 영향을 고려하는 것이 중요하다. 제자리 정렬(in-place sort)은 추가적으로 필요한 저장 공간을 상수 크기로 제한하여 메모리 사용을 최소화하는 알고리즘으로, 이러한 효율성을 극대화하는 방식이다. 제자리 정렬은 메모리 제약이 있는 환경에서 특히 유용하며, 데이터 크기가 커질수록 메모리와 관련된 오버헤드를 줄이는 데 큰 기여를 한다.
교환 정렬 (Exchange Sort)
교환정렬(Exchange Sort)은 배열 내의 요소들을 순차적으로 비교하여 정렬 순서에 맞지 않는 경우 위치를 교환하는 방식으로 작동하는 간단한 정렬 알고리즘이다. 이 알고리즘은 이중 루프를 사용하여 모든 요소를 서로 비교한 후, 정렬되지 않은 경우 두 요소의 자리를 바꾸는 방식으로 배열을 정렬한다. 첫 번째 루프는 정렬의 기준이 되는 요소를 선택하고, 두 번째 루프는 그 요소와 이후의 모든 요소를 비교하여 조건에 맞는 경우 위치를 교환한다.
이 알고리즘의 시간복잡도는 최선, 평균, 최악의 경우 모두 O(n^2)로, 매우 비효율적이다. 이는 배열이 이미 정렬되어 있어도 모든 요소를 비교해야 하기 때문이다. 교환 연산은 3번의 데이터 할당 작업(임시 변수로 저장, 교환, 복원)을 필요로 하며, 이는 데이터 크기가 크거나 교환 횟수가 많아질수록 성능 저하를 초래한다. 교환정렬의 장점은 구현이 간단하고 이해하기 쉬운 구조라는 점이다. 하지만 많은 비교와 교환이 필요하기 때문에 데이터 크기가 작을 때만 실용적이며, 대규모 데이터셋에서는 선택정렬이나 삽입정렬과 같은 다른 알고리즘에 비해 효율성이 크게 떨어진다
void exchangesort(int n, keytype S[]) {
for (i = 1; i <= n-1; i++) {
for (j = i+1; j <= n; j++) {
if (S[j] < S[i]) {
// 두 값을 교환
temp = S[i];
S[i] = S[j];
S[j] = temp;
}
}
}
}
삽입 정렬 (Insertion Sort)

삽입 정렬(Insertion Sort)은 배열의 두 번째 요소부터 시작해 정렬되지 않은 부분에서 현재 요소를 선택하고 이미 정렬된 부분에서 적절한 위치를 찾기 위해 왼쪽으로 비교를 진행하며 삽입될 위치를 찾으면 해당 요소를 이동시켜 정렬 상태를 유지하는 알고리즘이다. 이 방식은 배열을 순차적으로 탐색하면서 정렬을 확장해 나가는 방식으로 동작하며, 데이터가 이미 정렬된 경우에는 효율적이나, 정렬되지 않은 경우에는 많은 비교와 이동이 발생할 수 있다.
예를 들어 배열 [5, 4, 3, 2, 1]을 삽입 정렬로 정렬하면 다음과 같이 동작한다:
- 첫 번째 반복에서 4를 5 앞에 삽입해 [4, 5, 3, 2, 1].
- 두 번째 반복에서 3을 적절한 위치로 삽입해 [3, 4, 5, 2, 1].
- 이후 반복을 통해 최종적으로 [1, 2, 3, 4, 5]로 정렬된다.
void insertionsort(int n, keytype S[]) {
index i, j;
keytype x;
for (i = 2; i <= n; i++) {
x = S[i];
j = i - 1;
while (j > 0 && S[j] > x) {
S[j + 1] = S[j];
j--;
}
S[j + 1] = x;
}
}
복잡도 분석
삽입정렬(Insertion Sort)의 복잡도는 비교 횟수와 데이터 할당 횟수를 기준으로 분석할 수 있다. 먼저, S[j]와 x를 비교하는 횟수를 기준으로 살펴보면, 최악의 경우는 배열이 역순으로 정렬된 상태이다. 이 경우, 각 삽입 값은 정렬된 부분의 모든 요소와 비교되므로, 인덱스 에 대해 i−1번의 비교가 이루어진다. 이를 전체로 합산하면 1+2+3+...+(n−1)이 되고, 수식으로는 n(n−1)/2로 나타낼 수 있다. 따라서 최악의 경우 시간복잡도는 O(n^2)이다.
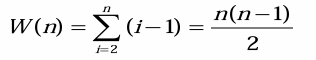
평균적인 경우 배열이 무작위로 섞여 있다고 가정하며 정렬된 부분의 절반 정도를 비교하게 된다.
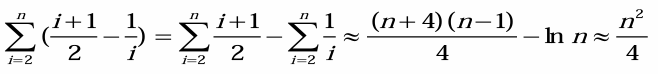
데이터 할당 횟수를 기준으로 살펴보면, 최악의 경우에는 배열이 역순으로 정렬된 상태로, 각 삽입 값이 정렬된 부분의 모든 요소를 오른쪽으로 이동시켜야 한다. 이는 인덱스 에 대해 최대 i−1번의 이동이 필요하며, 총 할당 횟수는 n(n−1)/2로 계산된다. 삽입 작업 자체도 한 번의 할당이 필요하므로, 최악의 경우 시간복잡도는 O(n^2)이다. 평균적인 경우에는 무작위로 섞인 배열을 가정하며, 한 값이 평균적으로 정렬된 부분의 중간 위치에 삽입된다고 보면, 평균 이동 횟수는 n24−n4로 계산된다. 이 역시 시간복잡도는 O(n^2)이다. 최선의 경우에는 배열이 이미 정렬되어 있어 값의 이동이 필요하지 않고, 삽입 작업에 한 번의 할당만 발생한다. 이 경우 총 할당 횟수는 n−1이며, 시간복잡도는 O(n)이다.

삽입정렬은 S[j]와 x의 비교 횟수와 데이터 할당 횟수 모두 배열의 초기 상태에 따라 성능이 크게 달라진다. 평균과 최악의 경우에는 시간복잡도가 O(n^2)로 비효율적이지만, 배열이 이미 정렬된 상태에서는 으로 효율적이다. 이러한 특성으로 인해 삽입정렬은 작은 데이터셋이나 정렬이 거의 완료된 배열에서 적합하며, 대규모 데이터에는 적합하지 않다.
선택 정렬 (Selection)

선택 정렬(Selection Sort)은 배열에서 정렬되지 않은 부분 중 가장 작은 값을 찾아 현재 위치의 요소와 교환하며 정렬을 수행하는 알고리즘이다. 첫 번째 요소부터 시작해 나머지 요소들 중 가장 작은 값을 찾아 교환하고, 정렬되지 않은 부분의 크기를 하나씩 줄이며 이 과정을 반복한다.
예를 들어, 배열 [29,10,14,37,13]을 선택 정렬로 정렬한다고 가정하면 다음과 같이 동작한다:
- 첫 번째 반복에서 [29, 10, 14, 37, 13] 중 가장 작은 값 10을 찾아 29와 교환한다 → [10,29,14,37,13].
- 두 번째 반복에서 나머지 부분 [29, 14, 37, 13] 중 13을 찾아 29와 교환한다 → [10,13,14,37,29].
- 이후 반복을 통해 배열이 완전히 정렬된다 → [10,13,14,29,37].
void selectionsort(int n, keytype S[]) {
index i, j, smallest;
// i는 배열에서 정렬이 완료된 구역과 미정렬 구역을 나누는 기준
for (i = 1; i <= n - 1; i++) {
// 현재 미정렬 구역에서 가장 작은 요소의 인덱스를 저장
smallest = i;
// 미정렬 구역의 요소들을 탐색
for (j = i + 1; j <= n; j++) {
// S[j]가 S[smallest]보다 작다면 smallest를 업데이트
if (S[j] < S[smallest]) {
smallest = j;
}
}
// 현재 i번째 요소와 smallest 위치의 요소를 교환
// 이 과정을 통해 i번째 위치에 가장 작은 요소를 배치
exchange S[i] and S[smallest];
}
}복잡도 분석
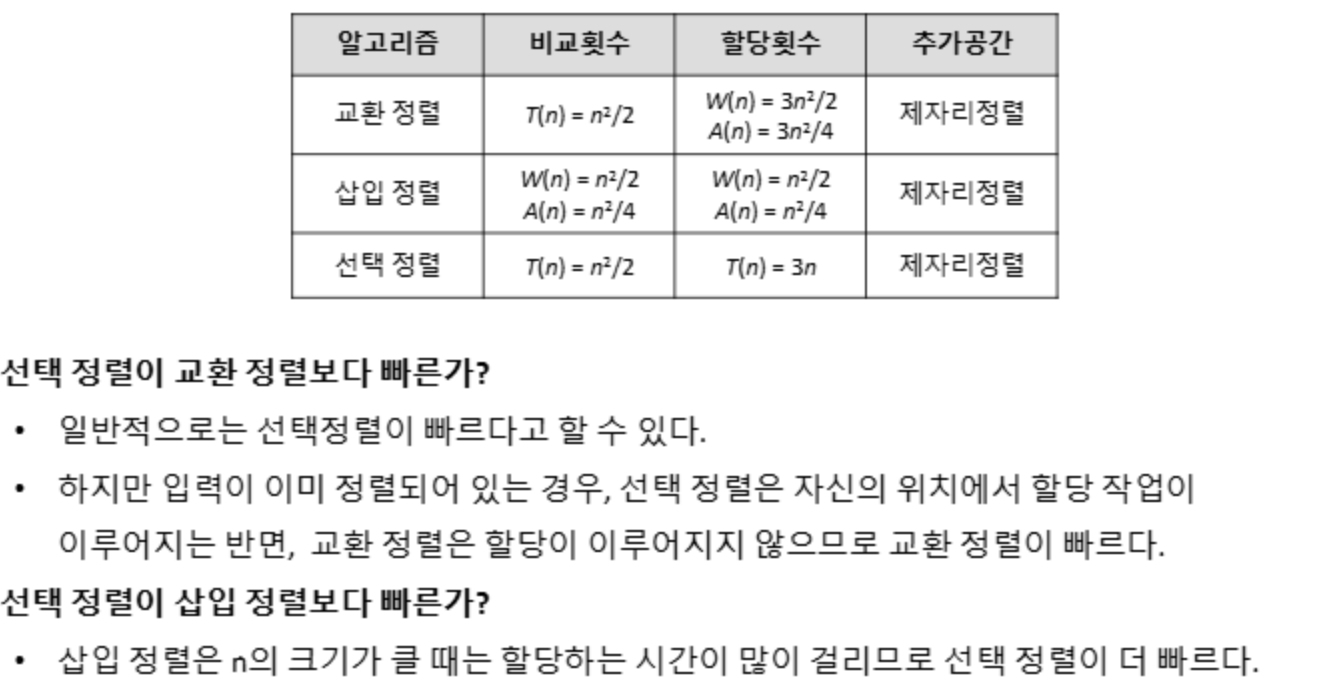
선택정렬의 시간복잡도는 입력 배열의 상태에 상관없이 항상 O(n^2)이다. 선택정렬은 정렬되지 않은 구역에서 가장 작은 요소를 찾아 정렬된 구역의 끝에 배치하는 과정을 반복하는 알고리즘으로, 비교 연산의 횟수는 입력 배열의 크기 n에 따라 일정하다. 구체적으로, i번째 단계에서 미정렬된 구역의 요소 개수는 n−i+1개이다. 이를 통해, i번째 단계에서 n−i번의 비교가 이루어진다. 이는 O(n^2)에 해당한다.
교환 연산의 경우, 각 단계에서 최대 한 번만 이루어진다. 따라서 교환 연산은 n−1번 수행되며, 이는 에 해당한다. 선택정렬은 제자리 정렬(In-place Sort)로 추가적인 메모리 공간을 필요로 하지 않아 공간복잡도는 O(1)이다. 다만, 선택정렬은 안정적인 정렬 알고리즘이 아니며, 동일한 값을 가진 요소의 순서가 변경될 수 있다.
힙 정렬

힙 정렬(Heapsort)은 완전 이진 트리의 특성을 활용하여 데이터를 정렬하는 비교 기반 정렬 알고리즘이다. 이 알고리즘은 힙(Heap)이라는 자료 구조를 사용하며, 특히 최대 힙(Max Heap)이나 최소 힙(Min Heap)을 기반으로 동작한다. 힙은 각 노드가 자식 노드보다 크거나(최대 힙) 작도록(최소 힙) 구성된 완전 이진 트리이며, 배열로 간단히 표현할 수 있다.

비교 한 번에 최대 하나의 역이 제거되는 알고리즘의 하한선
비교 기반 정렬 알고리즘에서, 역(inversion)이란 주어진 순열에서 i<j이고 k_i > k_j인 정수 쌍 (k_i, k_j)를 말한다. 예를 들어, 순열 [3, 2, 4, 1, 6, 5]에는 5개의 역, 즉 (3,2),(3,1),(2,1),(4,1),(6,5)가 존재한다. 정렬 알고리즘은 이러한 역을 제거하여 순열을 정렬한다. 만약 한 번의 비교로 하나의 역만 제거할 수 있다면, 최소 비교 횟수를 계산할 수 있다.
최악의 경우를 고려하면, 역의 총 개수인 최대 n(n−1)/2이다. 이는 순열이 역순으로 정렬된 상태일 때 발생한다. 따라서, 한 번의 비교로 하나의 역만 제거할 수 있는 알고리즘은 최악의 경우 최소 n(n−1)/2번의 비교를 필요로 한다. 예를 들어, 순열 [n,n−1,...,2,1]은 n(n−1)/2개의 역을 포함하며, 이 모든 역을 제거하기 위해서는 정확히 그만큼의 비교가 요구된다.
평균적인 경우를 계산할 때, 어떤 순열 P = [k_1, k_2, ..., k_n]에 대해, 그 전치(transpose) 순열 P_T = [k_n, ..., k_2, k_1]을 고려한다. P와 P_T에는 각각 역이 존재하며, 두 순열의 총 역 개수는 항상 n(n−1)/2이다. 따라서 P 또는 P_T 각각의 평균적인 역 개수는 n(n−1)/4이다. 이는 평균적으로 최소 n(n−1)/4번의 비교가 필요함을 의미한다.
결론적으로, 비교 한 번에 하나의 역만 제거할 수 있는 알고리즘의 하한선은 최악의 경우 n(n−1)/2번, 평균적인 경우 n(n−1)/4번의 비교가 필요하다. 교환, 삽입 정렬은 한번 비교할 때 기껏해야 하나의 역만을 제거할 수 있으므로 시간복잡도가 최악의 경우 n(n-1)/2 , 평균적으로는 n(n-1)/4 보다 좋을 수 없다.
합병정렬 알고리즘 재검토
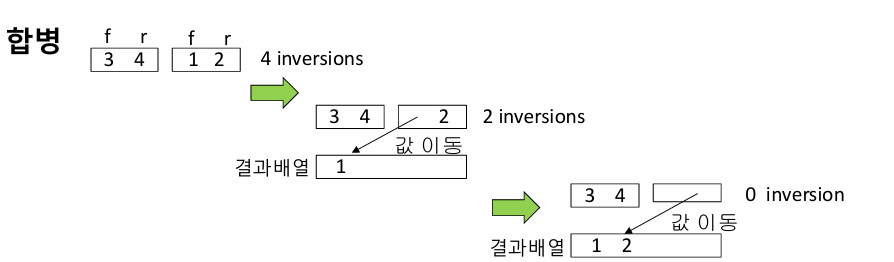
합병정렬은 비교마다 하나 이상의 역(inversion)을 제거할 수 있어, 한 번의 비교로 최대 하나의 역만 제거할 수 있는 교환 정렬이나 삽입 정렬보다 훨씬 효율적이다. 이는 합병 과정에서 여러 역이 한꺼번에 해결되기 때문이다.
주어진 두 배열이 [3,4]와 [1,2]라고 가정하자. 합병정렬에서는 이 두 배열을 비교하며 정렬된 상태로 하나의 결과 배열로 합친다. 먼저, 두 배열의 첫 번째 원소인 3과 1을 비교한다. 1이 더 작으므로 결과 배열에 추가된다. 이 비교는 단순히 3>1라는 한 번의 비교로 끝나지만, 동시에 (3,1)과 (4,1)이라는 두 개의 역이 제거된다.
다음으로, 과 를 비교한다. 가 더 작으므로 결과 배열에 추가된다. 이 과정에서도 (3,2)와 (4,2)라는 두 개의 역이 제거된다. 최종적으로 남은 3과 4는 이미 정렬된 상태이므로 추가 비교 없이 결과 배열에 삽입된다. 이 예시에서 확인할 수 있듯이, 합병정렬은 각 비교 과정에서 여러 역을 한꺼번에 제거하므로, 교환 정렬이나 삽입 정렬보다 더 적은 비교로 정렬을 완료할 수 있다. 이는 합병정렬의 효율성을 높이는 핵심 원리다.
힙 구조의 핵심 연산은 다음과 같다:
- 최대값 확인: 힙에서 최대값은 항상 뿌리 노드에 위치하므로 O(1)의 시간 복잡도로 확인할 수 있다.
- 최대값 제거 및 재구성: 최대값을 제거한 후, 힙의 성질을 유지하기 위해 재구성하는 작업은 O(logn) 시간이 걸린다.
- 데이터 추가, 삭제, 변경: 새로운 데이터를 삽입하거나 기존 데이터를 삭제 또는 수정할 때도 힙 구조를 유지해야 하므로 O(logn의 시간이 필요하다.

초기 힙 배열이 [10,9,8,7,3,2,1]이라고 하자. 이 상태에서 뿌리 노드인 10을 제거하고, 마지막 노드 1을 뿌리로 이동한다고 가정하자. 결과적으로 배열은 [1,9,8,7,3,2]가 된다. 이 배열에서 뿌리 노드 1은 힙 성질을 만족하지 않을 수 있으므로, Siftdown을 실행하여 힙 성질을 복구한다.
초기 상태: 배열: [1,9,8,7,3,2]
뿌리 노드 1이 힙 성질을 만족하는지 확인한다.
첫 번째 비교: 뿌리 노드 11과 두 자식 노드 9, 을 비교한다. 두 자식 중 더 큰 값은 이다. 1<9이므로, 1과 9를 교환한다. 배열 상태: [9,1,8,7,3,2]
두 번째 비교: 새롭게 이동한 노드 의 위치를 확인한다. 현재 노드 1의 자식 노드는 7과 3이다. 두 자식 중 더 큰 값은 77이다. 1<7이므로, 1과 7을 교환한다. 배열 상태:
세 번째 비교: 다시 이동한 노드 1의 위치를 확인한다. 현재 노드 1의 자식 노드는 없다. 자식 노드가 없으므로 더 이상 Siftdown을 진행하지 않는다.
힙 정렬 아이디어
1. n개의 키를 이용하여 힙을 구성한다 (makeheap)
2. 뿌리에 있는 제일 큰 값을 제거하고힙 재구성한다 (root)
3. Step 2를 n-1번 반복한다.
1. Siftdown
void siftdown(heap& H, index i) {
index parent, largerchild;
keytype siftkey;
bool spotfound;
siftkey = H.S[i];
parent = i;
spotfound = false;
while (2 * parent ≤ H.heapsize && !spotfound) {
if (2 * parent < H.heapsize && H.S[2 * parent] < H.S[2 * parent + 1])
largerchild = 2 * parent + 1;
else
largerchild = 2 * parent;
if (siftkey < H.S[largerchild]) {
H.S[parent] = H.S[largerchild];
parent = largerchild;
} else {
spotfound = true;
}
}
H.S[parent] = siftkey;
}
2. 최대값 추출(root)
keytype root(heap& H) {
keytype keyout;
keyout = H.S[1];
H.S[1] = H.S[H.heapsize];
H.heapsize = H.heapsize - 1;
siftdown(H, 1);
return keyout;
}
3. 키 제거(removekeys)
void removekeys(int n, heap& H, keytype S[]) {
index i;
for (i = n; i ≥ 1; i--)
S[i] = root(H);
}
4. 힙 생성(makeheap)
void makeheap(int n, heap& H) {
index i;
H.heapsize = n;
for (i = ⌊n / 2⌋; i ≥ 1; i--)
siftdown(H, i);
}
5. 힙 정렬 실행(heapsort)
void heapsort(int n, heap& H, keytype S[]) {
makeheap(n, H);
removekeys(n, H, S);
}
복잡도 분석
힙 정렬의 시간 복잡도는 두 가지 주요 단계인 makeheap과 removekeys를 중심으로 분석된다. makeheap은 주어진 데이터를 힙 구조로 변환하는 과정이다. 완전 이진 트리에서 깊이가 d인 노드는 최대 2^d개의 노드를 포함하며, 각각의 노드는 깊이에 따라 siftdown 연산이 수행된다. siftdown은 특정 노드를 아래로 이동시키며 힙의 성질을 만족시키는 작업으로, 한 번 수행할 때 최대 logn의 비교가 필요하다. 그러나 모든 노드가 동일한 횟수로 siftdown 되는 것은 아니며, 상위 깊이의 노드는 비교가 적고 하위 깊이의 노드는 비교가 많아진다. 이러한 점을 고려하여 전체 트리에 대해 siftdown 작업의 총 횟수를 계산하면, makeheap 단계는 O(n)의 시간 복잡도를 가진다.
예를 들어, 입력 데이터가 [4, 10, 3, 5, 1]일 때, 초기 배열을 힙 구조로 만들기 위해 siftdown을 적용한다. 가장 하위 레벨부터 시작하여 위로 올라가며 노드를 재배치한다. 먼저 [5, 1] 서브트리에 대해 siftdown을 적용하여 힙 구조를 만족하게 만들고, 그다음 [4, 10, 3] 부분에서 siftdown을 수행한다. 이를 통해 최종적으로 [10, 5, 3, 4, 1]이라는 힙 구조가 생성된다.
removekeys 단계는 힙에서 최댓값을 추출하고 힙을 재구성하는 작업을 반복하는 과정이다. 최댓값은 항상 힙의 루트에 위치하며, 이를 결과 배열에 저장한 뒤 마지막 노드를 루트로 이동시키고, 다시 siftdown을 통해 힙 성질을 복원한다. 이 과정은 logn번의 비교가 필요한 siftdown 연산을 n−1번 반복하므로, 총 시간 복잡도는 O(nlogn)이다.
예를 들어, 위에서 생성된 힙 [10, 5, 3, 4, 1]에 대해 최댓값 10을 추출한 뒤, 마지막 노드 1을 루트로 이동시키고 siftdown을 적용하면 [5, 4, 3, 1]로 재구성된다. 이 과정을 반복하여 최종적으로 [1, 3, 4, 5, 10]과 같이 오름차순으로 정렬된 배열을 얻는다.
힙 정렬의 전체 시간 복잡도는 두 단계를 합쳐 O(n+nlogn)=O(nlogn)이다. 이는 최악의 경우에도 동일한 시간 복잡도를 가지며, 비교 기반 정렬 알고리즘 중 최적에 해당한다. 공간 복잡도 측면에서, 힙 정렬은 배열 내에서 작업을 수행하므로 추가적인 저장 공간이 거의 필요하지 않다. 예컨대, 퀵 정렬이 종종 추가적인 재귀 호출 스택 공간을 필요로 하는 반면, 힙 정렬은 이러한 제약이 없어 O(1)의 공간 복잡도를 갖는다.
이러한 특성으로 인해 힙 정렬은 시간 복잡도와 공간 효율성이 모두 중요한 상황에서 특히 유용하다. 다만, 정렬된 데이터가 입력으로 주어졌을 때도 동일한 작업이 수행되기 때문에 최적화된 경우에도 항상 O(nlogn)의 성능을 보이며, 이는 데이터 분포에 따라 성능이 달라질 수 있는 퀵 정렬보다 상대적으로 느릴 수 있다.
기수 정렬

기수 정렬(Radix Sort)은 데이터를 비교하지 않고 정렬하는 비교 기반 외의 정렬 알고리즘이다. 정수나 문자열과 같은 구조적 데이터를 정렬할 때 효율적으로 작동하며, 데이터의 각 자리(digit)나 문자(character)를 기준으로 정렬한다. 기수 정렬은 주로 안정적인 보조 정렬 알고리즘과 결합하여 사용된다.

기수 정렬의 핵심 아이디어는 가장 낮은 자리수(Least Significant Digit, LSD)부터 시작해 점진적으로 높은 자리수(Most Significant Digit, MSD)로 이동하며 데이터를 정렬하는 것이다. 예를 들어, 숫자 배열을 정렬할 때 1의 자리, 10의 자리, 100의 자리 순서로 각각의 숫자를 기준으로 데이터를 그룹화하고 정렬한다. 문자열 정렬의 경우 가장 오른쪽 문자부터 왼쪽으로 진행하면서 그룹화한다. 기수 정렬의 주요 과정은 다음과 같다:
- 정렬할 데이터의 최대 자릿수를 확인한다.
- 가장 낮은 자리수부터 시작해 각 자리수를 기준으로 데이터를 분류한다.
- 이 과정을 반복하며 데이터를 정렬된 순서로 쌓아간다.
이 과정에서 각 자릿수 기준의 정렬은 안정적인 정렬 알고리즘, 예를 들어 카운팅 정렬(Counting Sort)을 사용한다. 이 안정성을 통해 기수 정렬은 이전 단계의 정렬 결과를 유지하며, 데이터의 원래 순서를 보존할 수 있다. 기수 정렬의 시간 복잡도는 정렬할 데이터의 길이 , 데이터의 자리수 d, 그리고 각 자리의 값 범위 k에 따라 O(d⋅(n+k))이다. 이때 자리수 d가 작고 값 범위 k가 제한적일수록 효율적이다. 따라서, 데이터의 크기가 큰 경우라도 값의 범위가 좁으면 기수 정렬이 매우 빠르게 동작한다.
기수 정렬은 비교 기반 정렬 알고리즘(예: 힙 정렬, 병합 정렬)이 가지는 Ω(nlogn)의 하한을 초과하지 않는 효율적인 정렬 방식이다. 다만, 기수 정렬은 정렬 과정에서 추가 메모리 공간을 요구하며, 데이터의 값 범위가 클 경우 비효율적일 수 있다. 이러한 특성으로 인해, 기수 정렬은 특정 조건에서만 효과적인 정렬 방법으로 사용된다.
기수 정렬 과정 설명
예제: 정수 배열 [170, 45, 75, 90, 802, 24, 2, 66]
정렬할 숫자의 최대 자릿수는 3이다(802는 세 자리수). 따라서, 각 자리수별로 정렬을 진행한다.
Step 1. 1의 자리수를 기준으로 정렬 (LSD):
- 각 숫자의 1의 자리수를 추출:
170 → 0, 45 → 5, 75 → 5, 90 → 0, 802 → 2, 24 → 4, 2 → 2, 66 → 6. - 숫자를 1의 자리수를 기준으로 정렬:
[170, 90, 802, 2, 24, 45, 75, 66].
Step 2. 10의 자리수를 기준으로 정렬:
- 각 숫자의 10의 자리수를 추출:
170 → 7, 90 → 9, 802 → 0, 2 → 0, 24 → 2, 45 → 4, 75 → 7, 66 → 6. - 숫자를 10의 자리수를 기준으로 정렬:
[802, 2, 24, 45, 66, 170, 75, 90].
Step 3. 100의 자리수를 기준으로 정렬:
- 각 숫자의 100의 자리수를 추출:
802 → 8, 2 → 0, 24 → 0, 45 → 0, 66 → 0, 170 → 1, 75 → 0, 90 → 0. - 숫자를 100의 자리수를 기준으로 정렬:
[2, 24, 45, 66, 75, 90, 170, 802].
최종 정렬된 배열: [2, 24, 45, 66, 75, 90, 170, 802]
복잡도 계산
시간 복잡도: O(d(n + k))
- d: 최대 자리수 (위 예시에서는 d = 3)
- n: 정렬할 데이터의 개수 (배열 길이)
- k: 각 자리수 값의 범위 (10진법에서는 k = 10)
공간 복잡도: 보조 배열을 사용하므로 O(n + k)
기수 정렬은 비교 기반 정렬이 아니므로 Ω(nlogn)의 하한을 초과하지 않고 더 빠를 수 있다.
기수 정렬은 다음 조건에서 매우 효율적이다:
- 데이터 크기가 크지만 자릿수가 작을 때
- 값의 범위가 좁을 때

'Computer Scinece > Programming Principles' 카테고리의 다른 글
| Programming Principles [7] : 탐색 알고리즘 (Search Algorithms) (0) | 2024.10.30 |
|---|---|
| Programming Principles [6] : 최적화 알고리즘 (Optimization Algorithms) (1) | 2024.09.18 |
| Programming Principles [5] : 재귀 알고리즘 (Recursive Algorithm) (0) | 2024.09.18 |
| Programming Principles [4] : 자료 구조 (Data Structures) (0) | 2024.09.18 |
| Programming Principles [3]: 데이터 추상화와 리스트 (Data Structures & List) (1) | 2024.09.18 |