1. 동적 계획법 (Dynamic Programming)
지금까지 알고리즘의 기본 원리와 분할 정복 알고리즘에 대해 배웠다. 분할 정복 알고리즘은 하향식(top-down) 접근 방식을 통해 문제를 해결하며, 나누어진 부분 문제들 간에 상관관계가 없는 경우에 적합하다. 그러나 피보나치 수열 계산과 같은 경우, 분할된 문제들이 서로 연관되어 있어 같은 항 를 여러 번 계산하게 된다. 이로 인해 효율성이 저하되므로, 분할 정복법은 피보나치 알고리즘과 같은 연관된 문제를 해결하는 데 적합하지 않다.

동적 계획법(dynamic programming)은 상향식(bottom-up) 접근 방식을 사용하는 알고리즘으로, 문제를 나눈 후 각 부분 문제를 먼저 해결하는 방식이다. 이 방법은 인덱스를 효과적으로 설정하여 작은 문제의 중복 해결을 방지하고, 작은 문제의 해결 결과를 바탕으로 더 큰 문제를 해결하는 구조를 가진다. 동적 계획법을 적용할 때는 먼저 재귀 관계식을 정립하고, 작은 사례부터 차례로 해결하여 그 결과를 이용해 복잡한 문제를 해결해 나간다. 이러한 절차를 통해 효율적으로 문제를 해결할 수 있다.

1. 재귀 관계식을 정립 : 2차원 배열 B를 만들고, 각 B[i][j]에는 iCj값을 저장하도록 한다. 그 값은 관계식으로 계산한다.

2. nCk를 구하기 위해서는 다음과 같이 B[0][0]부터 시작하여 위에 서 아래로 재귀 관계식을 적용하여 배열을 채워 나가면 된다. 결국 값은 B[n][k]에 저장된다.

최적의 원칙 (Principle of Optimality)
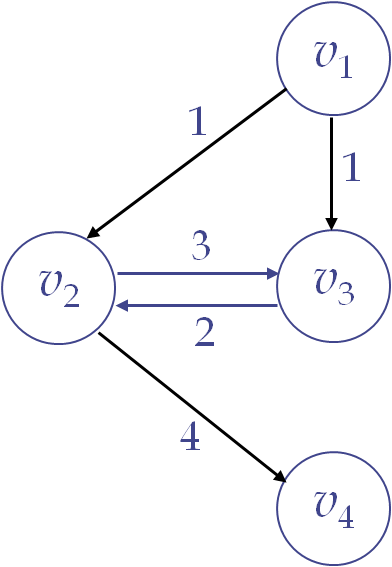
최적의 원칙이 적용되려면, 문제의 최적 해가 그 문제를 부분 문제로 나누었을 때 각 부분 문제에 대한 최적 해를 포함해야 한다. 예를 들어, 최단 경로 문제에서는 한 경로의 최적 해에 포함된 부분 경로들도 반드시 최적이어야 하므로, 동적 계획법을 사용할 수 있다. 하지만 모든 문제가 최적의 원칙을 따르지는 않는다. 예를 들어, 최장 경로 문제에서 순환이 없는 경로만 고려할 경우, v1에서 v4로 가는 최장 경로는 [v1, v3, v2, v4]이지만, 그 부분 경로인 v1에서 v3까지의 최장 경로는 [v1, v2, v3]으로 달라진다. 이처럼 부분 경로가 전체 경로의 최적 해가 아니기 때문에 최적의 원칙이 적용되지 않고, 동적 계획법을 사용할 수 없다.
요약하자면, 최적의 원칙이 적용되는 문제에서는 부분 문제에 대한 최적 해가 전체 문제의 최적 해를 포함하지만, 최적의 원칙이 적용되지 않는 경우(예: 최장 경로 문제)에는 부분 문제의 최적 해가 전체 최적 해와 일치하지 않아 동적 계획법을 사용할 수 없다.
이항 계수 알고리즘
1) 이항 계수 알고리즘 (분할 정복)
이항 계수 nCk는 n!/(k!(n−k)!)로 정의되며, 분할 정복을 통해 재귀적으로 계산할 수 있다. 이 방법에서는 이항 계수의 성질인 nCk=(n−1)C(k−1)+(n−1)Ck를 사용하여, 기본적인 재귀를 통해 문제를 작은 부분 문제로 나누어 해결한다. 재귀는 k=0이거나 k=n일 때 종료 조건으로, 이 경우 nCk=1이 된다.

이항 계수를 분할 정복으로 구하는 알고리즘은 작성하기는 간단하지만 비효율적이다. 그 이유는 동일한 계산을 여러 번 반복하기 때문인데, 예를 들어, bin(n−1,k−1)과 bin(n−1,k)을 구할 때, 두 재귀 호출 모두에서 bin(n−2,k−1)을 중복 계산하게 된다. 이처럼 동일한 부분 문제를 여러 번 계산하기 때문에 시간이 많이 소요된다. 이 알고리즘이 계산하는 항의 개수는 대략 2n에 가깝기 때문에 시간 복잡도는 O(2^n)로 매우 비효율적이다. 이러한 문제를 해결하려면 중복 계산을 방지하는 동적 계획법(DP)을 사용해야한다. (일정 시간복잡도 : 2 x nCk- 1)
int bin(int n, int k) {
if (k == 0 || n == k)
return 1;
else
return bin(n-1,k-1) + bin(n-1,k)
}
2) 이항 계수 알고리즘 (동적 계획)
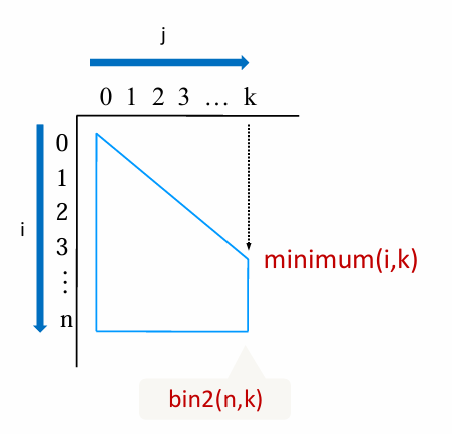
이항 계수를 동적 계획법으로 계산하는 방법은 2차원 배열을 활용하여 중복 계산을 방지하는 방식이다. 먼저, B[i][j]에 iCj 값을 저장하는 배열을 생성하고, 배열의 첫 번째 행과 대각선에 해당하는 값인 B[i][0]=1로 초기화한다. 그 후, 재귀 관계식 B[i][j]=B[i−1][j−1]+B[i−1][j]를 사용하여 B[0][0]부터 B[n][k]까지 순차적으로 값을 채워나간다. 이 방식은 각 부분 문제를 한 번씩만 계산하므로 시간 복잡도를 O(n×k)로 줄여 효율적으로 이항 계수를 구할 수 있다. 최종 결과는 B[n][k]에 저장된다.
• 단위연산: for-j루프 안의 B[i][j] 대입 연산
• 입력의 크기: n, k
• 일정 시간복잡도 분석 :

int bin2(int n, int k) {
index i, j;
int B[0..n][0..k];
for(i=0; i <= n; i++)
for(j=0; j <= minimum(i,k); j++)
if (j==0 || j == i)
B[i][j] = 1;
else
B[i][j] = B[i-1][j-1] + B[i-1][j];
return B[n][k];
}
최단 경로 찾기 알고리즘
그래프 이론
그래프 이론에서, 정점(노드)는 정보를 나타내며, 간선(엣지)는 정점 간의 연결을 의미한다. 방향 그래프(Directed Graph)는 간선이 특정 방향을 가지며, 간선이 한 정점에서 다른 정점으로만 연결되는 그래프이다. 가중치(Weight)는 간선에 할당된 값으로, 가중치 포함 그래프(Weighted Graph)에서는 각 간선이 특정 비용이나 거리를 나타낸다.
경로(Path)는 한 정점에서 시작해 다른 정점으로 이어지는 일련의 정점들로, 경로를 따라가는 동안 각 정점을 잇는 간선이 존재해야 한다. 예를 들어, 정점 A에서 B를 거쳐 C로 이동할 수 있다면 A→B→C가 하나의 경로가 됩니다. 순환(Cycle)은 하나의 정점에서 시작하여 다른 여러 정점을 거쳐 다시 시작 정점으로 돌아오는 경로이다. 예를 들어, A→B→C→A가 순환이다. 이때 순환 그래프(Cyclic Graph)는 이러한 순환을 포함하는 그래프이고, 반대로 순환이 없는 비순환 그래프(Acyclic Graph)도 있다.
길이(Length)는 경로 상의 간선 수를 의미한다. 가중치가 없는 그래프에서 경로의 길이는 단순히 거치는 간선의 개수로 정의되며, 예를 들어 A→B→C 경로의 길이는 2이다. 가중치 포함 그래프에서는 경로 상의 모든 간선의 가중치 합이 경로의 길이가 된다. 예를 들어, 간선 A→B의 가중치가 3이고 B→C의 가중치가 5라면, 경로 A→B→C의 길이는 8이 된다.
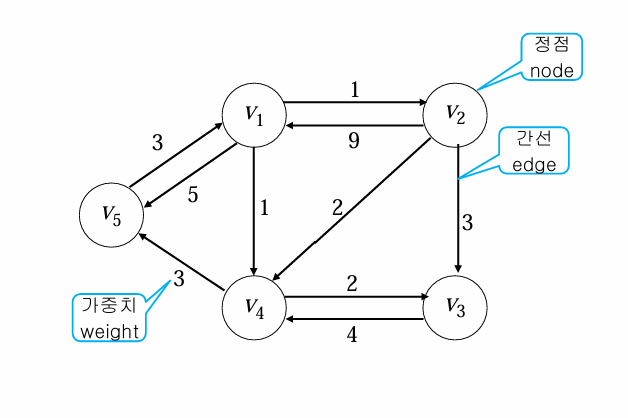
최단 경로 찾기 문제 (all-pairs Shortest Paths Problem)
최단 경로 찾기 문제는 가중치가 있는 방향성 그래프에서 한 정점에서 다른 정점으로 가는 가장 짧은 경로를 찾는 최적화 문제이다. 이 문제는 모든 정점 쌍에 대해 최단 경로를 계산해야 하며, 예를 들어 여러 도시를 연결하는 교통망에서 두 도시 간 가장 짧은 경로를 구하는 것과 유사하다. 최적화 문제란 여러 해답 중 가장 최적인 해답을 찾는 문제를 의미하며, 최단 경로 찾기 문제는 이와 같은 성질을 지닌다. 대표적인 예로는 지하철 노선에서 두 역 간 최단 경로를 찾는 문제가 있다.
1) 무작정 알고리즘 (Brute-Force Algorithm)으로 최단 경로 찾기
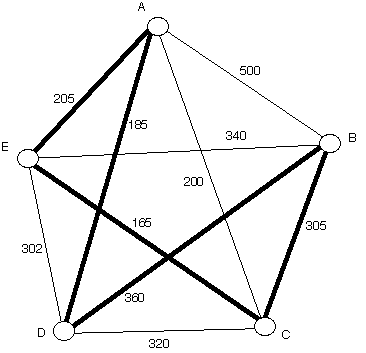
무작정 알고리즘(브루트 포스 알고리즘)을 사용해 최단 경로를 찾는 방식은, 정점 vi에서 다른 정점 vj로 가는 가능한 모든 경로를 계산한 후, 그 중에서 최소 길이의 경로를 선택하는 방식이다. 그래프에 개의 정점이 있고 모든 정점 간에 간선이 존재한다고 가정하면, vi에서 vj로 가는 경로의 수는 매우 많다. 특히 n−2개의 중간 정점을 모두 거치는 경로만 계산해도 가능한 경로의 수는 (n−2)!에 이르며 이 외에도 더 적은 정점을 거치는 경로까지 모두 확인해야 한다. 경로의 수가 지수 함수보다 훨씬 크기 때문에, 이러한 방식은 계산량이 폭발적으로 증가하여 비효율적이며 실질적으로 사용할 수 없다.
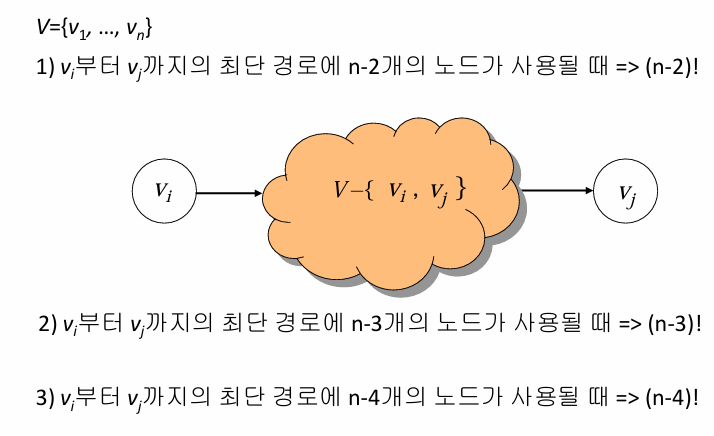
2) 동적 계획법으로 최단 경로 찾기
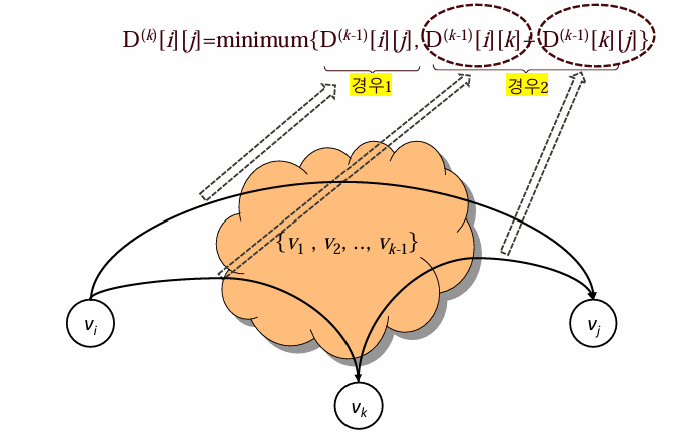
동적 계획법을 사용하여 최단 경로를 찾는 방법은 그래프의 인접 행렬을 이용하여 반복적으로 최단 경로를 갱신하는 방식이다. 주어진 그래프에서 각 정점 쌍 사이의 최단 거리를 계산하는 플로이드-와샬 알고리즘에 기반하는데 먼저 그래프의 초기 상태인 인접 행렬 W를 설정하고, 이때 경로가 없으면 무한대(∞)로 표기한다. 그런 다음, 정점 k를 차례대로 추가하며, 경로에 포함된 정점들을 고려하여 각 정점 에서 j로 가는 최단 경로를 갱신한다.

즉, 번째 정점을 거치지 않은 경로와 거치는 경로 중 최단 경로를 선택하여 갱신한다. 예를 들어, 주어진 그래프에서 v2에서 v5로 가는 경로를 찾는 과정을 살펴보면, 초기 상태 D(0)[2][5]는 경로가 없으므로 무한대이다. k=1일 때는 v1을 거치는 경로를 고려하여 D(1)[2][5]=min(∞,14)=14가 됩니다. k=4일 때는 v4를 경유하는 경로를 계산하여 D(4)[2][5]=min(14,5)=5로 최단 거리가 갱신됩니다. 이를 반복하여 최종적으로 D(5)[2][5]=5최단 경로입니다.요약하자면, 동적 계획법을 사용한 최단 경로 탐색은 각 정점을 차례대로 경로에 포함시키며, 경유하는 경우와 그렇지 않은 경우를 비교하여 최단 경로를 반복적으로 갱신하는 방식입니다.
1) 플로이드 최단 경로 알고리즘 1

플로이드 알고리즘은 모든 정점에서 다른 모든 정점까지의 최단 경로를 구하는 동적 계획법 기반의 알고리즘으로 그래프가 방향성과 가중치를 가질 때 사용된다. 알고리즘은 먼저 주어진 가중치 그래프를 기반으로 초기 경로 배열을 설정하고 중첩된 반복문을 통해 각 정점을 경유지로 삼아 경로를 갱신한다. 갱신 규칙은 정점 에서 로 가는 직접 경로와 정점 를 경유하는 경로 중 더 짧은 것을 선택하는 방식으로 이루어지며 최종적으로 각 정점에서 다른 모든 정점까지의 최단 거리가 포함된 배열이 생성된다. 시간 복잡도는 O(n^3)이다.
• 단위 연산: for-j 루프안의 지정문
• 입력 크기: 그래프에서의 정점의 수 n
• 일정 시간복잡도 분석 : T ( n ) = n * n * n = O(n*3)
void floyd(int n, const number W[][],number D[][]) {
int i, j, k;
D = W;
for(k=1; k <= n; k++)
for(i=1; i <= n; i++)
for(j=1; j <= n; j++)
D[i][j] = minimum(D[i][j], D[i][k]+D[k][j]);
}
2) 플로이드 최단 경로 알고리즘 2

플로이드 알고리즘에서 출력 배열은 두 가지로 구성된다. 최단 거리 배열 D와 경로 추적 배열 . 배열 D[i][j]는 정점 i에서 정점 j까지의 최단 경로 길이를 나타내고, 배열 P[i][j]는 에서 로 가는 최단 경로에 있는 중간 정점을 기록합니다. 만약 최단 경로에 중간 정점이 존재하면 그 중 가장 큰 인덱스의 정점을 P[i][j]에 저장하고, 중간에 정점이 없다면 P[i][j]=0으로 설정됩니다. 이 배열을 통해 경로의 정확한 구성도 추적할 수 있습니다.
void floyd2(int n,const number W[][],number D[][],index P[][]) {
index i, j, k;
for(i=1; i <= n; i++)
for(j=1; j <= n; j++)
P[i][j] = 0;
D = W;
for(k=1; k<= n; k++)
for(i=1; i <= n; i++)
for(j=1; j<=n; j++)
if (D[i][k] + D[k][j] < D[i][j]) {
P[i][j] = k;
D[i][j] = D[i][k] + D[k][j];
}
}
3) 최단 경로 출력

voidpath(index i,j) {
if (P[i][j] != 0) { // vi와 vj 사이 정점 없음
path(i,P[i][j]);
cout<< “ v” << P[i][j];
path(P[i][j],j);
}
}
연쇄 행렬 곱셈
연쇄 행렬 곱셈 문제에서는 여러 개의 행렬을 곱할 때, 곱셈 순서에 따라 필요한 총 곱셈의 횟수가 달라진다. 예를 들어, A1(10×100), A2(100×5), A3(5×50) 행렬을 곱할 때, (A1 × A2) × A3 순서로 곱하면 총 7,500번의 곱셈이 필요하지만, A1 × (A2 × A3) 순서로 곱하면 75,000번의 곱셈이 필요하다. 따라서 곱셈 횟수를 최소화하는 최적의 곱셈 순서를 결정하는 알고리즘을 개발하는 것이 목표이다.

연쇄 행렬 곱셈의 무작정 알고리즘은 가능한 모든 곱셈 순서를 고려하여 그중 최소 곱셈 횟수를 선택하는 방식이다. 하지만 이 방법의 시간 복잡도는 지수 시간으로 비효율적이다. n개의 행렬에 대해 마지막으로 곱하는 행렬이 무엇이냐에 따라 나머지 행렬들을 곱할 수 있는 순서의 가지 수는 tn-1개씩 존재하며, 이를 반복적으로 계산하면 tn ≥ 2tn-1이 되고, 이를 계속 확장하면 tn은 최소한 𝜃(2^n)의 복잡도를 갖는다는 사실을 알 수 있다.
연쇄 행렬 곱셈 문제에서 동적 계획법을 적용하려면 최적의 원칙이 성립해야 한다. 즉, n개의 행렬을 곱하는 최적의 순서가 있다면, 그 순서 속에 포함된 부분 행렬들 또한 최적의 순서를 가져야 한다. 예를 들어, 6개의 행렬 A1, A2, A3, A4, A5, A6를 곱할 때, 전체 최적의 순서가 A1 × ((((A2 × A3) × A4) × A5) × A6)라면, A2에서 A4까지 곱하는 최적의 순서는 반드시 (A2 × A3) × A4가 되어야 한다. 이처럼 부분 문제의 최적해가 전체 문제의 최적해에 포함되므로 동적 계획법을 사용할 수 있다.
설계 전략
연쇄 행렬 곱셈 문제에서 동적 계획법을 적용하기 위해서는 재귀 관계식을 사용한다. n개의 행렬 A1, A2, ..., An이 있을 때, 곱셈 횟수를 최소화하는 최적의 순서를 구하려면 각 부분 행렬 집합을 나누어 각각의 최적 경로를 찾아야 한다.
예를 들어, A1 × A2 × A3 × A4를 곱한다고 할 때, 먼저 A1에서 A4까지의 최소 곱셈 횟수 m[1,4]를 구하려면 다음과 같은 재귀 관계식을 사용한다:
- A1과 (A2 × A3 × A4)로 나눈 경우
- (A1 × A2)와 (A3 × A4)로 나눈 경우
- (A1 × A2 × A3)와 A4로 나눈 경우
이 각각의 부분문제에 대해 최소 곱셈 횟수를 구해 비교하면, m[1,4]는 각 경우의 최소 값을 선택하게 된다. 이렇게 부분 문제를 해결해 전체 문제를 최적화하는 방식이 재귀 관계식에 따른 동적 계획법의 적용 예다.
5. 연쇄 행렬 곱셈 알고리즘
int minmult(int n, const int d[], index P[][]) {
index i, j, k, diagonal;
int M[1..n][1..n];
for(i=1; i <= n; i++)
M[i][i] = 0;
for(diagonal = 1; diagonal <= n-1; diagonal++)
for(i=1; i <= n-diagonal; i++) {
j = i + diagonal;
}
return M[1][n];
i
M[i][j]= mini<=k<=j-1(M[i][k]+M[k+1][j]+ d[i-1]*d[k]*d[j]);
P[i][j] = 최소값을 주는 k의 값
}void order(index i, index j) {
if (i == j)
cout << “A” << i;
else {
k = P[i][j];
cout << “(”;
order(i, k);
order(k+1, j);
cout << “)”;
}
}이진 검색 트리 (Binary Search Tree, BST)
이진 검색 트리는 각 노드가 하나의 키를 가지며, 왼쪽 부분 트리의 모든 키는 부모 노드의 키보다 작거나 같고, 오른쪽 부분 트리의 모든 키는 부모 노드의 키보다 크거나 같은 구조를 가진 이진 트리이다. 이는 순서가 있는 집합(ordered set)의 키들로 구성되어 있어 데이터를 효율적으로 검색, 삽입, 삭제할 수 있도록 해준다. 각 노드에서 왼쪽 및 오른쪽 자식 노드는 해당 노드의 키와 비교하여 정렬된 형태를 유지하여, 이진 검색의 특성을 이용해 O(log n) 시간 복잡도로 효율적인 탐색이 가능하다.
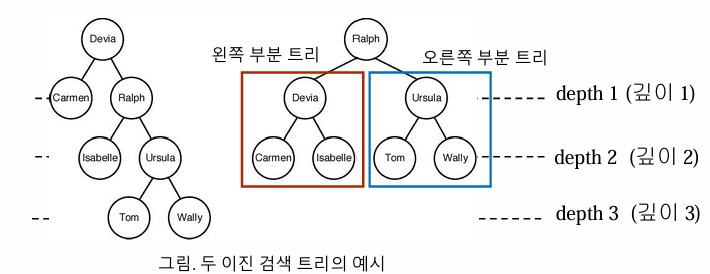
• 최적 이진 검색 트리: 키를 찾는데 걸리는 평균시간이 최소가 되도록 구축된 트리
• 최적 이진 검색 트리 문제: 각 키를 찾을 확률이 주어져 있을 때(모두 같지는 않음을 가정) 키를 찾는데 걸리는 평균시간이 최소가 되도록 이진 트리를 구축하는 문제
알고리즘
1. 이진 검색 트리의 검색
최적 이진 검색 트리를 구하기 위해 입력으로 주어진 키의 개수 nn과 각 키를 찾을 확률 pp (여기서 p[i]p[i]는 키 KeyiKey_i를 찾을 확률)를 사용하여 최적의 평균 검색 시간을 계산합니다. 이 과정은 DP(Dynamic Programming) 접근 방식을 통해 진행되며, 각 서브트리에 대한 최소 평균 검색 비용을 계산하여 minavgminavg를 도출합니다. 동시에, 행렬 RR을 구축하여 R[i][j]R[i][j]가 키 KeyiKey_i부터 KeyjKey_j까지를 포함하는 최적 트리의 루트 노드를 나타내도록 합니다. 최종적으로, 이 알고리즘을 통해 구한 최소 평균 검색 시간 minavgminavg와 함께 최적 트리를 구성하는 행렬 RR을 출력합니다.


• 단위 연산: k의 각 값에 대해 실행하는 명령문
• 입력 크기: 키의 개수 n
• 일정 시간복잡도 분석

void optsearchtree(int n, const float p[], float& minavg, index R[][] ){
index i, j, k, diagonal;
float A[1..n+1][0..n];
for( i=1; i<=n; i++)
A[i][i-1]=0; A[i][i]=p[i]; R[i][i]=i; R[i][i-1]=0;
A[n+1][n]=0;
R[n+1][n]=0;
for(diagonal=1; diagonal<=n-1; diagonal++){
for(i=1; i<=n-diagonal; i++){
j = i+diagonal;
j
A[i][j] = mini≤k≤j(A[i][k-1]+A[k+1][j])+
R[i][j] = 최소값을 주는 k의 값;
}
minavg = A[1][n];
2. 최적 이진 검색 트리 구축
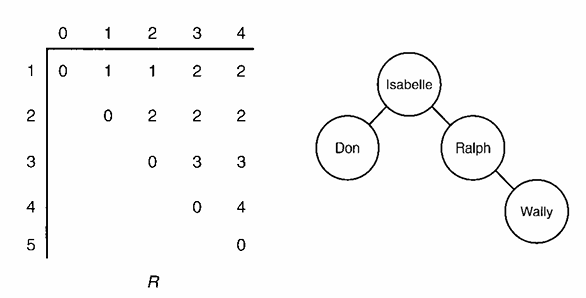
최적 이진 검색 트리를 구축하는 과정은 주어진 키의 개수 nn과 키를 순서대로 나열한 배열 KeyKey, 그리고 알고리즘 3.9에서 생성된 행렬 RR을 기반으로 진행됩니다. 이 과정은 DP(Dynamic Programming)를 사용하여 각 키에 대해 최적의 서브트리를 선택하는 방법으로 이루어집니다. 주어진 키 배열을 통해 각 키의 깊이를 고려하여 최적의 루트를 결정하고, 행렬 RR을 사용하여 서브트리의 구조를 구성합니다. 최종적으로, 이 과정을 통해 최적 이진 검색 트리를 생성하고, 생성된 트리를 가리키는 포인터 treetree를 출력하게 됩니다. 이를 통해 평균 검색 시간이 최소화된 효율적인 이진 검색 트리를 얻을 수 있습니다.
node_pointer tree (index i, index j) {
index k;
node_pointer p;
k = R[i][j];
if (k == 0)
return NULL;
else {
p = new nodetype;
p->key = Key[k];
p->left = tree(i, k-1);
p->right = tree(k+1, j);
return p;
}
2. 그리디 알고리즘 (Greedy Algorithms)

그리디 알고리즘은 각 결정 단계에서 그 순간에 가장 좋은 선택을 하여 최종적인 해답에 도달하는 방법이다. 이 알고리즘의 특징은 각 선택이 국소적으로는 최적이라고 판단되지만, 이러한 선택들이 모여서 형성된 전체 해답이 항상 글로벌 최적 해답이 되지는 않는다는 것이다. 따라서 탐욕 알고리즘을 사용할 때는 이러한 순간적인 선택들이 결과적으로 최적의 해답을 제공하는지 반드시 검증해야 한다.
탐욕 알고리즘 설계 절차
1. 선정 절차 (Selection Procedure)
이 단계에서는 현재 상태에서 가장 좋은 선택을 하여 해답 모음에 포함시킵니다. 탐욕 알고리즘의 핵심은 주어진 문제에 대한 최적 선택을 하는 것입니다.
예시:
최소 신장 트리(MST)를 찾는 프림 알고리즘을 고려해봅시다.
- 현재 정점에서 연결된 가장 가벼운 간선을 선택하여 그 간선을 포함시키고, 연결된 정점을 해답 모음에 추가합니다.
- 예를 들어, 정점 A에서 B, C, D로 가는 간선의 가중치가 각각 1, 3, 4일 때, A에서 가장 가벼운 간선인 A-B(가중치 1)를 선택합니다.
2. 적정성 점검 (Feasibility Check)
선택한 해답이 문제의 제약 조건을 만족하는지를 확인합니다. 즉, 새로운 해답 모음이 유효한지를 판단합니다.
예시:
프림 알고리즘의 경우, 선택한 간선이 사이클을 형성하지 않는지 확인합니다.
- 만약 A에서 B를 선택한 후, B에서 다시 A로 가는 간선이 선택된다면 이는 사이클이므로 적정성을 만족하지 않습니다.
- 따라서 A-B 간선 선택 후 B에 연결된 다른 정점으로 이동하여 추가적인 간선을 선택합니다.
3. 해답 점검 (Solution Check)
최종 해답이 최적의 해인지 검토합니다. 이 단계에서는 선택한 해답이 문제의 최적 조건을 충족하는지 확인합니다.
예시:
프림 알고리즘을 계속 진행하여 모든 정점이 연결되었고, 최종적으로 생성된 트리가 최소 신장 트리인지 확인합니다.
- 모든 정점을 포함하고, 사이클이 없으며, 가중치 합이 최소인 경우 최적의 해가 됩니다.
- 최종 트리가 더 나은 해가 될 수 있는 가능성이 없는지, 다른 경로로 더 낮은 가중치의 트리가 생성될 수 있는지 확인합니다.
결론
탐욕 알고리즘은 이와 같은 절차를 통해 문제를 해결합니다. 순간적인 선택이 항상 최적의 해답을 보장하지는 않지만, 적정성과 해답 점검 단계를 통해 전체 해답의 유효성을 검증할 수 있습니다.
프림 알고리즘 (Prim Algorithm)

프림(Prim) 알고리즘은 최소 비용 신장 트리(MST)를 찾기 위한 그리디 알고리즘입니다. 시작 정점을 선택한 후, 인접행렬로 표현된 비방향 그래프에서 정점 간의 가중치를 기반으로 가장 작은 가중치를 가진 간선을 선택하여 MST를 점차 확장해 나갑니다. nearest 배열은 이미 선택된 정점 집합 Y에 속한 정점 중에서 각 정점에 가장 가까운 정점을 기록하고, distance 배열은 해당 정점과의 최소 가중치를 저장합니다. 처음에는 임의의 정점에서 시작하여, distance 배열을 통해 최소 가중치를 가진 정점을 찾고 이를 Y에 추가합니다. 반복하면서 선택된 정점들과의 간선 가중치를 갱신하며, 이를 통해 최종적으로 모든 정점이 연결된 최소 신장 트리를 구성합니다.
신장 트리 (Spanning Tree)

연결된 비방향성 그래프 GG에서 신장트리는 모든 정점을 포함하면서 트리 구조를 이루는 연결된 부분그래프입니다. 신장트리를 얻기 위해 그래프 GG의 간선을 제거할 때, 순환을 형성하지 않도록 간선을 선택적으로 제거하여 각 정점이 연결되도록 해야 합니다. 이 과정에서 모든 정점이 포함되면서 연결성이 유지되므로, 신장트리는 GG의 모든 정점을 포함한 상태로 최소한의 간선으로 연결된 구조를 형성하게 됩니다.
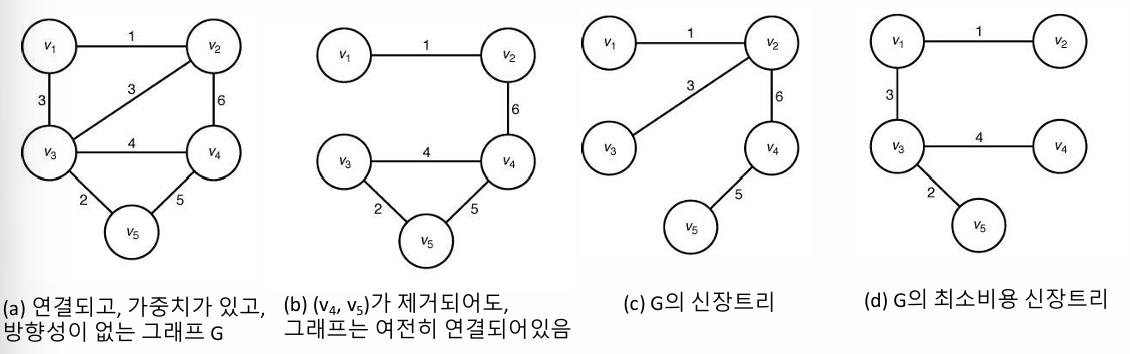
신장트리 중에서 가중치가 최소인 부분그래프를 최소비용 신장트리(MST)라고 하며, 이 최소 가중치의 부분그래프는 반드시 트리 구조를 가져야 합니다. 만약 최소비용 신장트리가 아니라면, 순환 경로가 존재하게 되고 이 경우 순환 경로 상의 한 간선을 제거함으로써 가중치가 더 작은 부분그래프를 형성할 수 있습니다. 이는 MST의 정의에 위배되므로, 최소비용 신장트리는 항상 순환을 포함하지 않는 트리 형태를 유지해야 합니다.
무작정 알고리즘
모든 신장트리를 고려하여 그 중에서 최소비용의 신장트리를 선택하는 알고리즘은 최악의 경우 지수 시간 복잡도를 가지며 매우 비효율적입니다. 정점의 수 nn에 대해 신장트리의 개수는 최대 nn−2n^{n-2}로, 이는 케일리 공식에 의해 알려진 결과입니다. 예를 들어, 정점이 4개일 경우 총 16개의 신장트리가 존재하게 되므로, 이 알고리즘은 모든 가능한 신장트리를 탐색해야 하므로 비현실적으로 많은 계산량을 요구하게 됩니다.
그리디 알고리즘
최소비용 신장트리(MST)를 찾기 위한 탐욕 알고리즘은 비방향성 그래프 G=(V,E)G = (V, E)에서 간선 집합 F⊆EF \subseteq E를 만족하면서, (V,F)(V, F)가 MST가 되도록 하는 간선을 찾는 과정입니다. 알고리즘은 먼저 FF를 빈 집합으로 초기화한 후, 최종 해답을 얻지 못할 때까지 다음 절차를 반복합니다: 첫째, 적절한 최적해 선정 절차를 통해 하나의 간선을 선택하고, 둘째, 선택한 간선을 FF에 추가해도 사이클이 생기지 않는다면 FF에 추가합니다. 마지막으로, T=(V,F)T = (V, F)가 신장트리인지 확인하고, 그렇다면 이를 사례 해결로써 최소비용 신장트리로 인정합니다. 이 과정을 통해 탐욕 알고리즘은 MST를 효과적으로 구축할 수 있습니다.

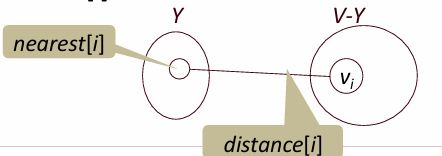
프림(Prim) 알고리즘은 최소 신장 트리를 찾기 위해 그래프의 인접 행렬 표현을 사용하는 방법입니다. 이 알고리즘에서는 간선의 가중치를 나타내는 이차원 배열 W[i][j]W[i][j]를 사용하며, W[i][j]W[i][j]는 정점 viv_i와 vjv_j 사이의 가중치를 저장합니다. 만약 간선이 존재하지 않는다면 해당 값은 ∞(무한대)로 설정되고, 자기 자신을 연결하는 경우 W[i][i]W[i][i]는 0입니다. 비방향 그래프의 특성상 W[i][j]W[i][j]는 대칭적입니다. 추가적으로, nearest와 distance 배열을 활용하여, nearest[i]는 현재 집합 YY에 속한 정점 중에서 viv_i와 가장 가까운 정점의 인덱스를 저장하며, distance[i]는 viv_i와 nearest[i]를 연결하는 간선의 가중치를 나타냅니다. 이를 통해 프림 알고리즘은 최소 신장 트리를 구성하는 데 필요한 최적의 간선을 효율적으로 선택할 수 있습니다.
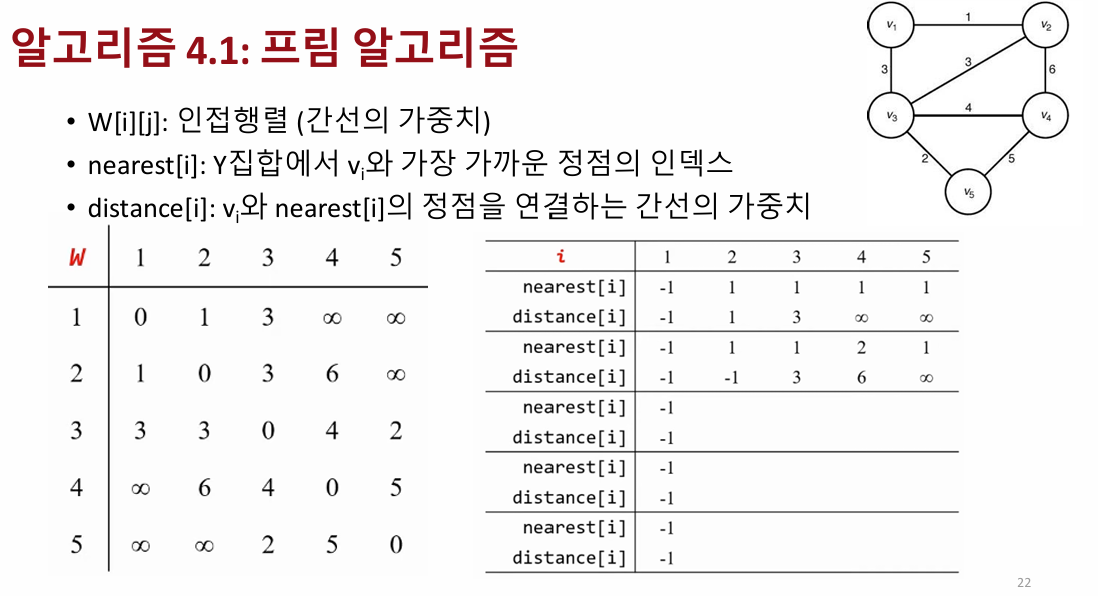
• 단위연산: repeat-루프 안에 있는 두 개의 for-루프 내부에 있는 명령문
• 입력크기: 정점의 개수n
프림 알고리즘의 시간 복잡도를 분석하면, 입력 크기인 정점의 개수를 n이라 할 때, 반복문은 n-1번 실행됩니다. 이 반복문 안에는 두 개의 for 루프가 있고, 각각 n-1번씩 실행되므로, 각 반복에서 실행되는 명령문들은 n-1번 반복됩니다. 이를 합치면 반복 루프 안의 명령문이 총 2(n-1)(n-1)번 실행됩니다. 따라서 시간 복잡도는 최종적으로 T(n) = 2(n-1)(n-1)이 되어, 이는 대략적으로 Θ(n^2)으로 표현할 수 있습니다. 즉, 입력 크기 n이 커질수록 알고리즘의 실행 시간은 대략 n^2에 비례하여 증가합니다
voidprim(intn, // 입력: 정점의 수
const number W[][], // 입력: 그래프의 인접행렬
set_of_edges& F) { // 출력: 그래프의 MST에 속한 간선의 집합
indexi, vnear; numbermin; edgee; indexnearest[2..n]; numberdistance[2..n];
F = ϕ;
for(i=2; i<= n; i++) { // 초기화
nearest[i] = 1; // vi에서 가장 가까운 정점을 v1으로 초기화
distance[i] = W[1][i]; // vi과 v1을 잇는 간선의 가중치로 초기화
repeat(n-1 times) {
min = ∞;
for(i=2; i <= n; i++)
if (0 <= distance[i] < min) {
min = distance[i];
vnear = i;
}
e = vnear와 nearest[vnear]를 잇는 간선;
e를 F에 추가;
distance[vnear] = -1;
for(i=2; i <= n; i++)
if (W[i][vnear] < distance[i]) {
distance[i] = W[i][vnear];
nearest[i]=vnear;
}
}
// n-1개의 정점을 Y에 추가한다
// 각 정점에 대해서
// distance[i]를 검사하여
// 가장 가까이 있는 vnear을
// 찾는다.
// 찾은 정점을 Y에 추가한다.
// Y에 없는 각 정점에 대해서
// distance[i]를 갱신한다.
}
다익스트라 알고리즘

다익스트라(Dijkstra) 알고리즘은 가중치가 있는 방향 그래프에서 하나의 시작 정점에서 다른 모든 정점까지의 최단 경로를 찾는 알고리즘입니다. 이 알고리즘은 먼저 시작 정점을 기준으로 각 정점까지의 최단 거리를 기록하는 배열을 생성하고, 아직 방문하지 않은 정점 중에서 가장 짧은 거리를 가진 정점을 선택하여 경로를 확장합니다. 각 정점을 탐색할 때마다, 그 정점과 인접한 정점들로 가는 새로운 경로를 계산하고, 기존 경로보다 짧으면 업데이트합니다. 이 과정을 모든 정점에 대해 반복하여 최종적으로 시작 정점에서 다른 모든 정점으로 가는 최단 경로를 구합니다.


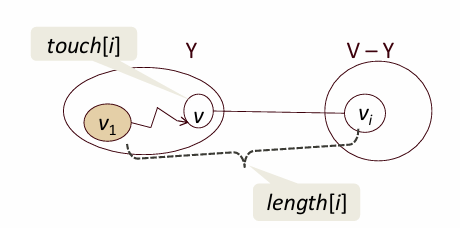
다익스트라(Dijkstra) 알고리즘은 최단 경로를 찾기 위해 그래프에서 특정 정점으로부터 다른 모든 정점까지의 거리를 계산하는 데 사용됩니다. 이 알고리즘에서는 두 가지 주요 배열인 touch와 length를 활용합니다. touch[i]는 최단 경로상에서 v1에서 vi(비-Y 정점)로 가는 경로에 포함된 마지막 Y 속한 정점을 나타내며, 이를 통해 경로의 중간 단계를 추적할 수 있습니다. length[i]는 v1에서 vi로 가는 최단 경로의 길이를 저장하며, 이 경로는 Y에 속한 정점들만 중간에 포함하도록 제한됩니다. 이 두 배열을 통해 알고리즘은 최적 경로를 효율적으로 찾고 업데이트할 수 있습니다.
단위연산: repeat-루프 안에 있는 두 개의 for-루프 내부에 있는 명령문
• 입력크기: 마디의 개수, n
voiddijkstra(intn, // 입력: 정점의 수
constnumberW[][], // 입력: 그래프의 인접행렬식 표현
set_of_edges& F) { // 출력: 최단경로 상에 놓여있는 간선의 집합
indexi, vnear;
edgee;
indextouch[2..n];
numberlength[2..n];
F = ϕ;
for(i=2; i<= n; i++) { // 각 정점에 대해서,
touch[i] = 1; // v1에서 출발하는 현재 최단경로의 마지막 정점을
length[i] = W[1][i]; // v1로 초기화 한다.
} // 그 경로의 길이는 v1에서의 간선 상의 가중치로
// 초기화한다
repeat(n-1 times) {
min = ∞;
for(i=2; i <= n; i++)
if (0 <= length[i] < min) {
min = length[i];
vnear = i;
}
e = (touch[vnear], vnear);
e를 F에 추가;
for(i=2; i <= n; i++)
// 최단경로를 가지는지 각 정점을 점검한다.
if (length[vnear]+ W[vnear][i] < length[i]) {
length[i] = length[vnear] + W[vnear][i];
touch[i] = vnear;
// Y에 속하지 않는 각 정점에 대해서,
}
length[vnear]=-1;
}
// 최단경로를 바꾼다.
// vnear가 인덱스인 정점을 Y에 추가한다.
48
}
허프만 코드 (Huffman Code)

허프만 코드는 데이터를 효율적으로 압축하기 위해 사용되는 최적 이진 코드이다. 이는 주어진 데이터 내 문자의 빈도수를 기반으로 필요한 비트 수를 최소화하도록 설계된 가변 길이 이진 코드이다. 허프만 코드는 Prefix 코드의 특성을 갖는데, 이는 어떤 문자의 코드워드가 다른 문자의 코드워드의 앞부분이 될 수 없음을 의미한다. 이러한 특성 덕분에 허프만 코드는 코드를 해석할 때 추가적인 구분 기호 없이도 올바르게 해석이 가능하다.
허프만 코드는 문자나 데이터를 효율적으로 저장하기 위한 방법으로, 자주 나타나는 문자는 짧은 코드로, 드물게 나타나는 문자는 긴 코드로 표현한다. 예를 들어, 어떤 문서에서 'a', 'b', 'c' 세 문자가 있다고 가정하자. 이 중 'a'는 10번, 'b'는 4번, 'c'는 2번 등장한다고 할 때, 'a'가 가장 많이 등장하므로 가장 짧은 코드(예: 0)를 부여하고, 'b'와 'c'는 각각 더 긴 코드(예: 10, 11)를 부여한다.
이렇게 만들어진 허프만 코드는 예를 들어 "abac"라는 문자열을 0, 10, 0, 11로 표현할 수 있다. 이는 총 6비트만 사용하며, 모든 문자를 동일한 길이의 코드로 표현하는 고정 길이 코드(예: 2비트씩 사용, 총 8비트 필요)보다 공간을 절약한다. 허프만 코드는 이렇게 문자의 등장 빈도에 따라 최적화된 코드를 만들어 효율성을 극대화하며, 파일 압축 알고리즘이나 데이터 전송에서 널리 사용된다.
허프만 코드 구축 방법
허프만 코드를 구축하는 방법은 간단한 과정을 통해 이진 트리를 만드는 것이다. 이를 예시로 설명해보겠다. 가령 문자 'a', 'b', 'c', 'd'가 있고, 각각의 빈도수가 10, 15, 30, 45라고 하자. 먼저 각 문자를 하나의 노드로 표현하고, 빈도수를 기준으로 우선순위 큐에 저장한다. 이 큐에서 가장 빈도수가 낮은 두 노드를 꺼내 새로운 노드를 생성하는데, 이 노드의 빈도수는 두 노드의 빈도수 합이다. 이렇게 생성된 노드는 다시 큐에 삽입된다.

이 예시에서 처음 두 노드 'a'(10)와 'b'(15)를 합쳐 빈도수 25의 새로운 노드를 만든다. 그다음 이 노드를 큐에 삽입하고, 남은 노드 중 가장 작은 두 노드 'c'(30)와 새로운 노드(25)를 병합하여 빈도수 55의 노드를 생성한다. 마지막으로 이 노드와 'd'(45)를 합쳐 최종적으로 빈도수 100의 이진 트리가 완성된다. 완성된 트리에서는 왼쪽 가지에 0, 오른쪽 가지에 1을 할당하여 각 문자에 대한 코드를 생성한다. 예를 들어, 'a'는 000, 'b'는 001, 'c'는 01, 'd'는 1로 표현될 수 있다. 이 방법은 빈도수가 높은 문자가 더 짧은 코드로 변환되도록 보장하며, 저장 공간을 크게 절약할 수 있게 한다.
허프만 코드 생성 알고리즘
허프만 코드 생성 알고리즘은 주어진 문자들의 빈도수를 기반으로 최적의 이진 트리를 구성하는 방법이다. 먼저, 각 문자를 빈도수와 함께 노드로 표현하고, 이를 우선순위 큐에 삽입한다. 우선순위 큐는 빈도수가 낮은 순서대로 정렬된다. 알고리즘은 빈도수가 가장 작은 두 노드를 큐에서 꺼내 병합하여 새로운 노드를 만든다. 이 새 노드의 빈도수는 병합된 두 노드의 빈도수 합이며, 이 노드는 다시 큐에 삽입된다. 이 과정을 모든 노드가 하나의 트리로 통합될 때까지 반복한다. 최종적으로 생성된 트리의 루트는 허프만 트리의 시작점이 된다.

예를 들어, 문자 'a', 'b', 'c', 'd'가 각각 빈도수 5, 9, 12, 13을 가진다고 하자. 처음에는 우선순위 큐에 각 문자를 삽입하고, 빈도수가 가장 작은 'a'(5)와 'b'(9)를 병합하여 빈도수 14의 새로운 노드를 생성한다. 이 노드를 큐에 삽입한 후, 다시 가장 작은 두 노드 'c'(12)와 '14'를 병합하여 빈도수 26의 노드를 만든다. 마지막으로 이 노드와 'd'(13)를 병합하여 빈도수 39의 최종 트리를 완성한다. 완성된 트리에서 각 문자는 경로에 따라 이진 코드로 변환된다. 예를 들어, 'a'는 경로 00, 'b'는 01, 'c'는 10, 'd'는 11로 표현될 수 있다. 이러한 과정은 데이터를 압축하는 데 유용하며, 빈도수가 높은 문자일수록 짧은 코드가 할당되어 저장 공간을 절약할 수 있다.
// 허프만 코드 생성 알고리즘의 슈도코드
struct nodetype {
char symbol; // 문자를 저장하는 변수
int frequency; // 문자의 빈도수를 저장하는 변수
nodetype* left; // 왼쪽 자식 노드의 포인터
nodetype* right; // 오른쪽 자식 노드의 포인터
};
// 우선순위 큐(Priority Queue)를 사용하여 노드들을 관리한다.
// 빈도수가 작을수록 높은 우선순위를 가진다.
for (i = 1; i <= n-1; i++) {
remove(PQ, p); // 빈도수가 가장 작은 노드를 우선순위 큐에서 제거
remove(PQ, q); // 두 번째로 빈도수가 작은 노드를 우선순위 큐에서 제거
r = new nodetype; // 새로운 노드를 생성
r->left = p; // p 노드를 r의 왼쪽 자식으로 설정
r->right = q; // q 노드를 r의 오른쪽 자식으로 설정
r->frequency = p->frequency + q->frequency; // 두 노드의 빈도수를 합산하여 r의 빈도수로 설정
insert(PQ, r); // 새로 생성된 노드를 우선순위 큐에 삽입
}
remove(PQ, r); // 최종적으로 큐에 남은 하나의 노드(루트 노드)를 제거
return r; // 허프만 트리의 루트 노드를 반환복잡도 분석
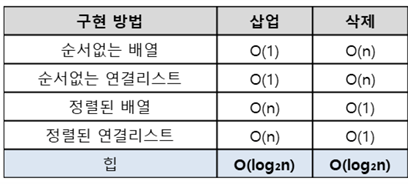
힙 기반 우선순위 큐를 사용할 경우 시간복잡도는 Θ(n lg n)
0-1 배낭 채우기 문제 (0-1 Knapsack Problem)

0-1 배낭 채우기 문제는 제한된 용량을 가진 배낭에 물건을 담아야 할 때, 선택한 물건들의 총 가치가 최대가 되도록 조합을 찾는 최적화 문제다. "0-1"이라는 이름은 물건을 선택하거나 선택하지 않는 두 가지 옵션만 가능하다는 의미를 가진다. 예를 들어, 3kg의 무게와 60의 가치를 가진 물건을 배낭에 넣을 수 있지만, 절반만 넣는 것은 허용되지 않는다.
문제는 다음과 같이 정의된다. 각 물건은 무게와 가치가 주어지고, 배낭에는 허용 가능한 최대 무게가 있다. 목표는 배낭의 무게 한도를 초과하지 않으면서 물건들의 총 가치를 최대화하는 것이다. 예를 들어, 배낭 용량이 5kg이고, 물건들이 각각 (무게 3kg, 가치 60), (무게 2kg, 가치 50), (무게 4kg, 가치 70)일 경우, 최적의 선택은 첫 번째와 두 번째 물건을 선택하는 것이며, 이때 총 무게는 5kg, 총 가치는 110이 된다.
이 문제를 해결하는 방법에는 여러 가지가 있다. 첫 번째는 모든 가능한 물건 조합을 탐색하는 브루트포스 방법이다. 하지만 물건이 개일 때 경우의 수가 2^n에 달하기 때문에 비효율적이다. 두 번째 방법은 그리디 알고리즘으로, 물건을 가치가 높은 순서 또는 무게 대비 가치가 높은 순서로 배낭에 담는다. 하지만 이 방법은 항상 최적해를 보장하지 않는다. 가장 효율적인 접근은 동적 계획법을 사용하는 것이다. 동적 계획법은 배낭의 용량과 선택한 물건의 수에 따라 부분 문제를 정의하고, 이를 기반으로 전체 문제를 해결한다. 배낭 용량 W와 물건 수 n에 대해 동적 계획법의 시간 복잡도는 O(n⋅W)로, 매우 효율적이다.
무작정 알고리즘(Brute Force)은 0-1 배낭 채우기 문제를 해결하기 위해 모든 가능한 조합을 탐색하는 방식이다. 이 접근법은 n개의 물건에 대해 모든 부분집합을 고려하며, 각 부분집합이 배낭의 무게 제한을 초과하지 않으면서 최대 가치를 제공하는지 확인한다. 예를 들어, 물건 집합이 {a,b,c}라면 가능한 조합은 빈 집합부터 {a,b,c}까지 총 2^n개가 된다. 이 방법은 단순하면서도 항상 최적해를 보장하지만, 시간 복잡도가 O(2^n)으로 매우 크기 때문에, 물건의 수가 많아질수록 계산량이 폭발적으로 증가한다.
탐욕 알고리즘(Greedy Algorithm)은 물건을 선택하는 데 있어 특정 기준을 정하고, 그 기준에 따라 우선적으로 물건을 배낭에 담는 방식이다. 예를 들어, 물건의 가치가 높은 순서, 무게가 가벼운 순서, 또는 무게당 가치가 높은 순서를 기준으로 정렬한 후, 배낭의 용량을 초과하지 않는 범위에서 가능한 한 많은 물건을 선택한다. 탐욕 알고리즘은 단순하고 빠르며 시간 복잡도가 O(nlogn)로 효율적이지만, 항상 최적해를 보장하지는 않는다. 예를 들어, 무게당 가치가 높은 물건부터 선택하는 방식에서는 일부 물건의 무게가 적합하지 않아 더 높은 총 가치를 놓칠 수 있다. 이로 인해 탐욕 알고리즘은 단순히 근사해를 제공하거나 특정 조건에서만 최적해를 보장할 수 있다.
0-1 배낭 채우기 문제 동적 계획법 알고리즘

동적 계획법을 이용한 배낭 채우기 문제 해결은 문제를 여러 작은 부분 문제로 나누어 각각의 최적해를 계산하고 이를 기반으로 전체 문제의 최적해를 도출한다. 이 방법은 각 부분 문제의 결과를 테이블에 저장하여 중복 계산을 방지한다. 문제는 테이블 P[i][w]로 표현되며, 여기서 P[i][w]는 처음 i개의 물건을 고려했을 때, 배낭 용량 에서 얻을 수 있는 최대 가치를 나타낸다. 이를 재귀적으로 정의하면, 현재 물건을 담을 수 없는 경우에는 이전 상태의 값을 그대로 가져오고( P[i−1][w] ), 담을 수 있는 경우에는 담는 경우와 담지 않는 경우 중 더 높은 가치를 선택한다( max(P[i−1][w],pi+P[i−1][w−wi] )
동적 계획법은 먼저 초기화 과정에서 배낭 용량이 0이거나 고려할 물건이 없을 때의 최대 가치를 0으로 설정한다. 이후 물건의 개수와 배낭 용량을 기준으로 테이블을 채워나가며, 각 단계에서 가능한 최대 가치를 계산한다. 예를 들어, 물건의 무게와 가치가 각각 (2kg, 3), (3kg, 4), (4kg, 5)이고 배낭 용량이 5kg인 경우, 동적 계획법은 각 물건의 선택 가능성을 비교하여 최적해인 총 가치 7을 도출한다.
이 방법의 시간 복잡도는 O(n⋅W)로, 무작정 알고리즘의 O(2^n)에 비해 훨씬 효율적이다.
knapsack(p, w, n, W) {
// 초기화: 배낭의 용량과 물건의 개수에 따라 DP 테이블 생성
// P[i][w]는 i번째 물건까지 고려했을 때, 무게 w에서의 최대 가치를 의미한다.
for(w = 0 to W)
P[0, w] = 0; // 물건이 없을 때 배낭의 가치는 항상 0
for(i = 0 to n)
P[i, 0] = 0; // 배낭의 용량이 0일 때 배낭의 가치는 항상 0
// DP 테이블 채우기: 물건과 배낭의 용량을 기반으로 최적 해 구하기
for(i = 1 to n) { // i는 현재 고려하는 물건의 인덱스
for(w = 0 to W) { // w는 현재 배낭의 용량
if(wi <= w) // 현재 물건의 무게 wi가 배낭 용량 w보다 작거나 같을 때
P[i, w] = max{P[i-1, w], pi + P[i-1, w-wi]};
// 물건 i를 포함하지 않는 경우(P[i-1, w])와
// 물건 i를 포함하는 경우(pi + P[i-1, w-wi]) 중 더 큰 값을 선택
else
P[i, w] = P[i-1, w]; // 현재 물건을 배낭에 포함할 수 없으므로 이전 최적 값을 그대로 사용
}
}
return P[n, W]; // n개의 물건과 배낭 용량 W를 고려했을 때의 최대 가치 반환
}
Python 코드
def knapsack(n, W, w, p):
P = [[0]*(W+1) for _ in range(n+1)]
for i in range(1, n+1):
for wt in range(W+1):
if w[i] <= wt:
P[i][wt] = max(P[i-1][wt], p[i] + P[i-1][wt - w[i]])
else:
P[i][wt] = P[i-1][wt]
return P[n][W]
# 예제 1
print("######Example 1######")
n, W = 3, 30
w = [0, 5, 10, 20]
p = [0, 50, 60, 140]
maxprofit = knapsack(n, W, w, p)
print("maxprofit: ", maxprofit)
동적 계획법 알고리즘 개선
개선된 방법은 공간을 최적화하는 데 초점을 맞춘다. 기본 알고리즘은 2차원 배열이기 때문에 O(n×W)의 공간을 사용하지만, 사실 특정 시점에서 P[i][w]를 계산하는 데 필요한 정보는 P[i−1][w] 뿐이다. 따라서 2차원 배열을 1차원 배열 P[w]로 축소할 수 있다.
개선된 알고리즘의 과정은 다음과 같다:
- 초기화: P[w] 배열을 0으로 초기화.
- 물건 i에 대해 역방향으로 배열 P[w]를 갱신. 이는 현재 항목이 업데이트된 값을 이전 단계에서 사용하는 것을 방지한다.
알고리즘의 최악의 경우 시간 복잡도는 여전히 O(n×W)이다. 하지만 공간 복잡도는 O(W)로 줄어든다.
Python 코드
def knapsack(n, W, DP):
global w, p
if n == 0 or W <= 0:
DP[(n, W)] = 0
else:
if w[n] > W:
DP[(n, W)] = knapsack(n - 1, W, DP)
else:
DP[(n, W)] = max(knapsack(n - 1, W, DP),
knapsack(n - 1, W - w[n], DP) + p[n])
return DP[(n, W)]
# Example 1
print("######Example 1######")
n, W = 3, 30
w = [0, 5, 10, 20]
p = [0, 50, 60, 140]
DP = {}
maxprofit = knapsack(n, W, DP)
print("maxprofit: ", maxprofit)
# Example 2 - Your Custom Case
print("######Example 2 #######")
# Insert your example here
n, W = 3, 50
w = [0, 5, 10, 20]
p = [0, 50, 60, 140]
DP = {}
maxprofit = knapsack(n, W, DP)
print("maxprofit: ", maxprofit)복잡도 분석
1. 각 물건의 무게가 다양할 경우 (wi가 1이 아님)
이 경우, n−i번째 행에서 2^i개의 상태를 계산해야 한다. 이는 각각의 선택에서 물건을 포함하거나 포함하지 않는 두 가지 경우를 따지기 때문이다. 결과적으로, n개의 물건에 대해 계산되는 항의 총 수는 다음과 같이 나타난다:
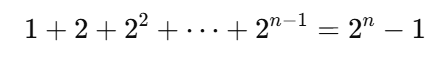
이는 기하급수적으로 증가하므로, 시간 복잡도는 Θ(2n)가 된다. 이는 문제를 단순히 무작정 탐색(Brute Force)하는 것과 동일한 수준으로 비효율적이다.
2. 각 물건의 무게가 1이고 n=W+1인 경우
이 경우, 각 w에 대해 정확히 한 번씩 상태를 계산한다. 즉, 를 순차적으로 증가시키며 각각의 상태를 업데이트한다. 이러한 경우 계산되는 항의 총 수는 다음과 같다:
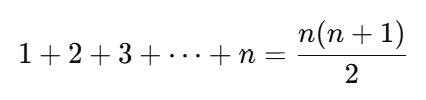
여기서 n=W+1이므로, 계산 항의 총 수는 (W+1)(n+1) / 2에 해당한다. 이는 Θ(nW)에 속한다.
3. 두 경우의 통합
최악의 경우 수행 시간은 앞서 언급한 두 가지 시나리오 중 더 작은 복잡도로 결정된다:
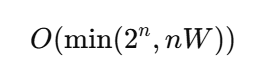
- 물건의 개수 n이 작고 각각의 무게가 다양하면 O(2^n)이 된다.
- 물건의 개수가 많고 모든 무게가 1이라면 O(nW)가 된다.
개선된 알고리즘은 특정 상황에서 Θ(2^n) 시간 복잡도를 가지지만, 일반적으로는 Θ(nW)수준에서 계산이 이루어진다. 이 분석은 문제의 입력 조건에 따라 알고리즘의 실제 성능이 크게 달라질 수 있음을 시사한다. 따라서 O(min(2n,nW))로 나타낸 시간 복잡도는 모든 경우의 최악의 복잡도를 표현한 것이다.

'Computer Scinece > Programming Principles' 카테고리의 다른 글
| Programming Principles [8] : 정렬 알고리즘 (Sortion Algorithms) (0) | 2024.12.03 |
|---|---|
| Programming Principles [7] : 탐색 알고리즘 (Search Algorithms) (0) | 2024.10.30 |
| Programming Principles [5] : 재귀 알고리즘 (Recursive Algorithm) (0) | 2024.09.18 |
| Programming Principles [4] : 자료 구조 (Data Structures) (0) | 2024.09.18 |
| Programming Principles [3]: 데이터 추상화와 리스트 (Data Structures & List) (1) | 2024.09.18 |