JaehyeonByun

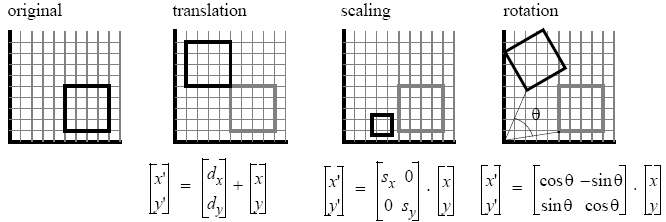
컴퓨터 그래픽스에서 변환(Transformation)은 3D 공간에서 객체의 위치, 방향, 크기를 조작하는 데 사용하는 수학적 연산으로 이동 변환, 회전 변환, 축소/확대 변환, 전단 변환, 투시 변환 등이 있다. 예를 들어, 게임 엔진에서는 이동 변환을 통해 캐릭터를 위치시킬 수 있고, 회전 변환으로 캐릭터의 방향을 조정하며, 축소/확대 변환으로 객체의 크기를 조절 할 수 있다. 구체적인 변환의 수학적인 행렬을 알아보기에 앞서 변환 그룹에 대한 이해를 해두는 것이 좋다, ​더보기Transformation Group 변환을 행렬로 간단하게 표현하기 위해선 잘 정리되어있는 성격이 필요한데, 변환 그룹의 세가지 성격을 서로 다른 변환들이 가지고 있다면 그 변환을 그룹으로 표현할 수 있다. 변환 그룹은 변환 ..

모델링은 모델링은 3D 공간에서 객체를 만드는 과정이다.​Polygon : 폴리곤은 폴리곤은 2D 공간 또는 3D 공간에서 선분으로 연결된 세 개 이상의 점으로 이루어진 폐곡선으로 3D 객체를 표현하는데 가장 기본적인 단위이다. 라인 루프로 닫혀진 오브젝트 이지만 내부를 가지고 있다. 폴리곤은 변의 수에 따라 n각형으로 분류되고 삼각형은 주로 게임 모델링, 사각형은 라이팅과 필름메이킹에 주로 이용된다.​Polygonal Mesh : Polygonal mesh는 3차원 컴퓨터 그래픽에서 polygon의 모음으로 이루어진 객체를 표현하는 데이터 구조로 각 다면체는 3개 이상의 점으로 구성되며, 이 점들은 선으로 연결되어 표면을 형성한다.​ (좌) Polygon의 종류와 (우) Triangle polygon으..

Computer Graphics컴퓨터 그래픽스는 3D 모델링, 렌더링, 애니메이션 등을 통해 컴퓨터 시스템에서 시각적 정보를 생성하고 조작하는 기술 분야이다. 빛의 물리학을 시뮬레이션 하여 컴퓨터로 사진같은 가상 그림을 만드는 것이라고 볼 수 있다.

1. 미분적분학의 발상James Steward Calculus미적분학은 고등학교 때부터 대학 전공 기초에 이르기까지 오랜 시간 공부해온 과목이지만, 그 본질에 대해 직관적으로 이해해야만 응용하고 적용할 수 있다. 미적분을 학습하는데에 중요한 것은 곱의 미분법, 연쇄 법칙, 음함수의 미분법, 미분과 적분의 관계, 테일러 급수같은 핵심 발상을 다루면서 그 많은 공식들이 실제로 어디에서 왔는지, 그것들이 의미하는 바는 무엇인지 포괄적인 시각적 접근을 통하여 명확히 이해해야한다. 마치, 수학을 발명한다는 감각을 느낄수 있어야 한다.큰 수가 작은 것들의 합으로 근사될 수 있는 문제들은 특정 그래프 아래의 면적에 관한 문제로 해결할 수 있다.미분적분학이 중요한 이유​Circle먼저 기하학의 매우 특정한 형태인 원의..

1 - The Essence of Linear AlgebraBased on the lecture by 3B1B Youtue, Professor Seunkyu Lee선형대수학을 전공기초 수업을 통해 배우기는 했지만 가우스 소거법, 크라메르 법칙같은 계산법과 문제 풀이에만 치중했을 뿐 행렬곱이 어떻게 정의되는지, 고윳값의 의미는 무엇인지 수학적인 본질은 이해하지 못했다. 후에 책과 유튜브를 통해 선형대수에 대해 다시 공부하면서, 선형대수는 수로써의 연산 뿐만 아니라 기하학 수준에서 이해하는 것이 매우 중요하다는 것을 알게 되었다.공간이라고 생각하면 직관이 먹힌다프로그래머를 위한 선형대수 - 히라오카 카즈유키 저선형대수를 시각화하여 이해하는 것은 그 본질을 파악함에 있어 유용한 방법이다. 따라서 Ruby로 직..

컴퓨터 비전은 디지털 이미지나 비디오에서 정보를 추출하고 해석하여 컴퓨터가 시각적 인식을 수행할 수 있도록 하는 기술이다. 급속도로 발전하고 있는 인공지능(AI)과도 밀접하게 연관되어 있으며 이미지 분류, 객체 인식, 얼굴 인식, 행동 인식, 의료 영상 분석 등의 분야에서 광범위하게 활용된다. 컴퓨터 비전 기술은 이미지 처리, 패턴 인식, 머신 러닝 등을 포함하여, 데이터에서 의미 있는 인사이트를 얻는 것을 목표로 한다. 컴퓨터 비젼은 카메라 데이터를 다룰 때와 3D 개발에서 매우 중요하다. 컴퓨터 비전 기술은 카메라를 통해 수집된 2D 이미지 데이터를 3D 정보로 변환하는 데 핵심적인 역할을 하는데, 예를 들어 스테레오 비전이나 깊이 카메라를 이용하여 물체의 거리와 위치를 측정하고 이를 통해 현실 세계..

1. 동적 계획법 (Dynamic Programming) 지금까지 알고리즘의 기본 원리와 분할 정복 알고리즘에 대해 배웠다. 분할 정복 알고리즘은 하향식(top-down) 접근 방식을 통해 문제를 해결하며, 나누어진 부분 문제들 간에 상관관계가 없는 경우에 적합하다. 그러나 피보나치 수열 계산과 같은 경우, 분할된 문제들이 서로 연관되어 있어 같은 항 f(i)를 여러 번 계산하게 된다. 이로 인해 효율성이 저하되므로, 분할 정복법은 피보나치 알고리즘과 같은 연관된 문제를 해결하는 데 적합하지 않다.  동적 계획법(dynamic programming)은 상향식(bottom-up) 접근 방식을 사용하는 알고리즘으로, 문제를 나눈 후 각 부분 문제를 먼저 해결하는 방식이다. 이 방법은 인덱스를 효과적으로 설정..

지금까지 C++ 문법을 통해 프로그래밍 언어의 기본적인 구문과 기능을 익히고, 객체지향 프로그래밍을 통해 소프트웨어의 구조와 설계를 이해하며, 자료구조를 통해 데이터를 효율적으로 관리하는 방법을 배웠다. 이제는 알고리즘을 통해 실제로 어떻게 데이터를 어떻게 문제를 해결할 것인지 배울 차례이다. 이를 통해 문제 해결에 필요한 논리적 사고와 최적화 기술을 더 깊이 있게 적용하여 효율적이고 유지보수 가능한 소프트웨어를 개발할 수 있을 것이다.  알고리즘(Algorithms)은 특정 문제를 해결하기 위해 명확하게 정의된 일련의 절차나 단계들을 의미한다. 알고리즘은 주어진 입력을 처리하여 원하는 출력으로 변환하는 방법을 체계적으로 설명하며, 컴퓨터 과학, 수학, 데이터 처리, 인공지능 등 다양한 분야에서 사용된다..

List​리스트는 순서가 있는 값들의 모음이다.선형 관계 (Linear Relationship) : 첫 번째 요소를 제외 한 각 요소에는 고유한 선행 요소가 있고 마지막 요소를 제외한 각 요소에는 고유 한 후속 요소가 있다길이 (Length) : list 안의 아이템의 개수; 길이는 프로그램 실행에 따라 달라질 수 있다.​Unsorted list vs Sorted list​1. Unsorted list : 데이터 항목들이 특정 순서 없이 저장되며 데이터 요소 간의 유일한 관계는 앞 요소과 뒤 요소 간의 관계이다. 즉, 어떤 데이터 뒤에 어떤 데이터가 있는지만 알 수 있고, 데이터 자체의 값에 따라 어떤 순서로 배열되어 있는지 알 수 없다.2. Sorted list : 데이터 항목들이 특정 키(key) 값..

Data Design and Implementation​Data type​Data : 데이터는 프로그래밍 세계의 명사로 객체는 조작되는 대상, 정보는 처리되는 대상이다. C++는 다양한 데이터 유형을 제공하며 기본적인 데이터 유형은 크게 내장 유형과 복합 유형이 있다.​내장 유형내장 유형은 프로그래밍 언어에 기본적으로 제공되는 데이터 유형이다. 프로그래머가 직접 정의하지 않고도 사용할 수 있는 유형이며, 일반적으로 언어의 가장 기본적인 데이터 요소를 나타낸다. 숫자형 , 문자열형, 논리형 , 불린형, 배열형, 객체형 등이 있다.​복합 데이터 유형(Composite Data Type)복합 데이터 유형은 여러 개의 기본 데이터 유형을 결합하여 만들어진 데이터 유형으로 기본 데이터 유형을 조합하여 더 복잡한 ..